-
Hola, alguien me puede ayudar con este ejercicio por favor, gracias.
Sabiendo que la estación espacial internacional gira alrededor de la Tierra
en una órbita de 386 km de altura sobre la superficie, calcular: (2 PUNTOS)
a. La velocidad lineal a la que orbita, expresada en km/h. (1p)
b. El tiempo que tarda en completar una órbita (0,5p)
c. La velocidad angular y lineal del planeta Tierra en su rotación. (0,5p)
Datos: M Tierra = 5,98·10 24 kg ; R Tierra = 6,37·10 6 m; G=6,67·10 -11 N·m 2 /kg 2


Antonio Silvio Palmitano
el 16/12/19Vamos con una orientación.
a)
Observa que la única fuerza que está aplicada sobre la Estación es la acción gravitatoria que la Tierra ejerce sobre ella, por lo que aplicas la Segunda Ley de Newton, y queda la ecuación:
G*MT*ME/Ro2 = ME*acp, divides por ME en ambos miembros, y luego despejas:
acp = G*MT/Ro2 (1), que es la expresión del módulo de la aceleración centrípeta de la Estación.
a)
Sustituyes la expresión del módulo de la aceleración centrípeta en función de la rapidez lineal y del radio orbital de la Estación, en la ecuación señalada (1), y queda:
v2/Ro = G*MT/Ro2, multiplicas por Ro y luego extraes raíz cuadrada positiva en ambos miembros, y queda:
v = √(G*MT/Ro) (2), que es la expresión de la rapidez lineal de la Estación.
b)
Sustituyes la expresión de la rapidez lineal en función del periodo orbital y del radio orbital de la Estación , en la ecuación señalada (2), y queda:
2π*Ro/To = √(G*MT/Ro), y de aquí despejas:
To = 2π*Ro/√(G*MT/Ro) (3), que es la expresión del periodo orbital de la Estación.
c)
Tienes el valor del periodo rotacional terrestre:
TT = 24 h = 24*3600 = 86400 s;
Tienes el radio orbital promedio de un punto de la superficie terrestre:
RT = 6,37*106 m.
Luego, planteas la expresión de la rapidez angular rotacional terrestre en función de sus periodo orbital, y queda:
ωT = 2π/TT (4).
Luego, planteas la expresión de la rapidez lineal orbital para un punto de la superficie terrestre, en función del radio de la Tierra y del periodo orbital del planeta, y queda:
vST = 2π*RT/TT (5).
Luego, solo queda que reemplaces valores en las ecuaciones numeradas y hagas los cálculos.
Espero haberte ayudado.
-
Me he visto videos de efecto doppler, me se la teoría pero este ejercicio no tengo por donde sacarlo.
Un observador, sobre un tren que se mueve a 40 m/s oye el silbato de otro que viaja delante, en igual sentido y percibe un sonido de una frecuencia de 800 Hz antes de adelantarle. Después de adelantarle oye una frecuencia 700 Hz. Calcula a) ¿Cuál es la velocidad del segundo tren? b) ¿la frecuencia del sonido emitido por la locomotora? c) ¿Cuál será la longitud de onda percibida por el observador del primer tren antes del adelanto? Dato Velocidad del sonido 340 m/s.


Breaking Vlad
el 22/12/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
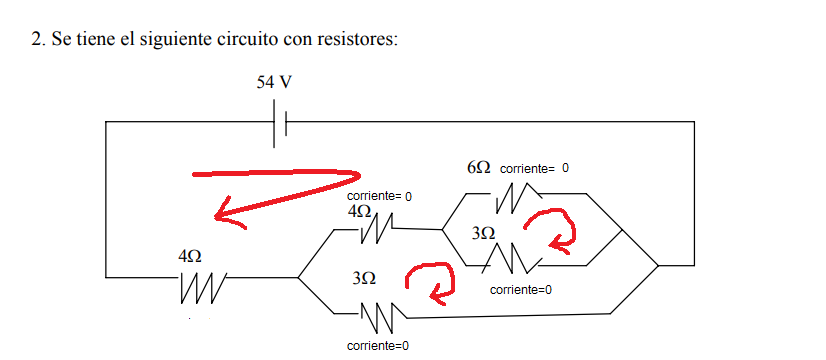
Buenas. tengo una pregunta respecto a hallar corriente en los resistores: hice los cálculos con las 3 mallas que dibuje en la imagen, cada maya representa una corriente, entonces en orden (de la maya mas pequeña a la mas grande, con sus corrientes: x,y,z respectivamente);
-6x - 3x = 0
-4y - 3*(y-x) - 3y = 0
-54 - 6*(z-x) - 4*(z-y) - 4z = 0
esto se reduciria a : 9x=0 ; 10y=3x ; 54=6x+4y-14z
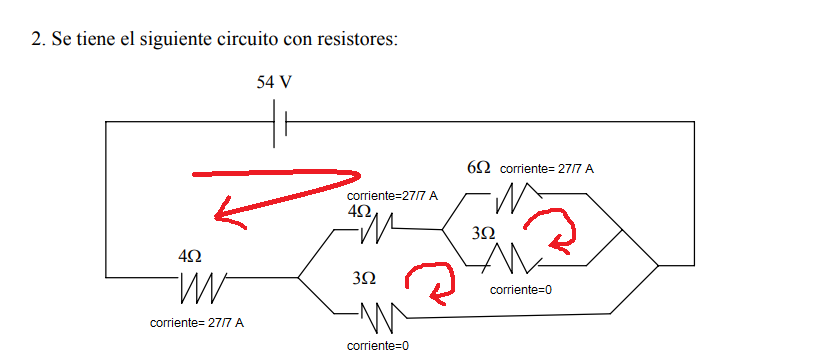
Esto indicaria que la corriente en la maya mas pequeña y mediana seria 0, y en la mas grande seria 27/7 A, y a la vez esto indicaria segun las primeras 2 ecuaciones que la corriente en los resistores (excepto 1) es como en la imagen
Pero entonces al involucrar la tercera ecuación me queda esto:
Tambien me di cuenta que si involucrara otra maya (la mas grande), me sale que la resistencia de 3 ohm (la mas externa) tiene corriente 54/7.....
Esta correcto, o estoy equivocado? porque me dan valores diferentes?


Antonio Silvio Palmitano
el 16/12/19Vamos con una orientación.
Observa que debes plantear cinco intensidades de corriente, que suponemos todas se dirigen de izquierda a derecha en sus tramos horizontales:
x: sale del borne positivo de la batería, y llega hasta el nudo más cercano al borne positivo;
y: sale del primer nudo y llega hasta el primer nudo en la rama superior;
z: sale del primer nudo, y llega hasta el tercer nudo recorriendo la rama inferior;
w: sale del primer nudo en la rama superior, recorre la rama superior de la malla más pequeña, y llega hasta el tercer nudo;
p: sale del primer nudo en la rama superior, recorre la rama inferior de la malla más pequeña, y llega hasta el tercer nudo.
Luego, aplicas la Primera Ley de Kirchhoff en el primer nudo, y queda:
x - y - z = 0 (1).
Luego, aplicas la Primera Ley de Kirchhoff en el primer nudo de la rama superior, y queda:
y = w + p (2).
Luego, aplicas la Segunda Ley de Kirchhoff para la malla más pequeña, y queda:
6w - 3p = 0 (3).
Luego, aplicas la Segunda Ley de Kirchhoff para la malla mediana, y queda:
4y + 3p - 3z = 0 (4).
Luego, aplicas la Segunda Ley de Kirchhoff para la malla principal, y queda
-4x - 4y - 6w - (-V) = 0, aquí multiplicas por -1 en todos los términos, reemplazas el valor de la fuerza electromotriz, y queda:
4x + 4y + 6w = 54 (5).
Luego, queda que resuelvas el sistema formado por las cinco ecuaciones numeradas, cuya solución es:
x = 9 A, y = 3 A, z = 6 A, w = 1 A, p = 2 A.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 17/12/19Recuerda que las Leyes de Kirchhoff son dos:
Ley de los Nudos (Primera Ley), de los que debes considerar uno menos que la cantidad total de nudos del circuito,
Ley de las Mallas (Segunda Ley), de las que debes considerar una menos que la cantidad total de mallas del circuito.
Luego, planteas una intensidad de corriente para cada tramo del circuito, y propones tú los sentidos de las mismas.
Luego, observa que en el circuito de tu enunciado tienes tres nudos, por lo que restas una unidad, y queda que debes tomar dos, y plantear una ecuación con cada uno de ellos.
Luego, observa que en el circuito de tu enunciado tienes cuatro mallas, por lo que restas una unidad, y queda que debes tomar tres, y plantear una ecuación con cada una de ellas.
Luego, observa que queda un sistema de cinco ecuaciones lineales, de primer grado y con cinco incógnitas, que son las intensidades de las corrientes en cada tramo del circuito.
Luego, resuelves el sistema, y tendrás los valores de las corrientes, y puedes tener una de dos situaciones para cada intensidad de corriente:
a)
si el valor de la corriente que has hallado es positivo, entonces tienes que el sentido de la corriente que has supuesto al inicio es correcto,
b)
si el valor de la corriente que has hallado es negativo, entonces tienes que el sentido de la corriente que has supuesto al inicio es incorrecto, por lo que la corriente en cuestión tiene el sentido opuesto al que has supuesto tú de antemano.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 13/12/19d)
Establece un sistema de referencia con eje OX paralelo a la rampa con sentido positivo hacia arriba, y con eje OY perpendicular a la rampa con sentido positivo hacia abajo, y observa que en el instante en que se suprime la fuerza F tienes que el sistema se desplaza hacia arriba.
Luego, aplicas la Segunda Ley de Newton para ambos cuerpos, y tienes el sistema de ecuaciones:
-M1*g*senθ - T = M1*a (1),
N1 - M1*g*cosθ = 0, de aquí despejas: N1 = M1*g*cosθ (2),
-M2*g*senθ + T = M2*a (3),
N2 - M2*g*cosθ = 0, de aquí despejas: N2 = M2*g*cosθ (4);
luego, divides miembro a miembro la ecuación señalada (1) entre la ecuación señalada (3), simplificas en el segundo miembro, y queda:
(-M1*g*senθ - T)/(-M2*g*senθ + T) = M1/M2, multiplicas por (M2*g*senθ + T) y por M2 en ambos miembros, y queda:
M2*(-M1*g*senθ - T) = M1*(-M2*g*senθ + T), distribuyes en ambos miembros, y queda:
-M2*M1*g*senθ - M2*T = -M1*M2*g*senθ + M1*T, multiplicas por -1 en todos los términos, y queda:
M2*M1*g*senθ + M2*T = M1*M2*g*senθ - M1*T, sumas M1*T y restas M2*M1*g*senθ en ambos miembros, y queda:
M1*T + M2*T = M1*M2*g*senθ - M2*M1*g*senθ,
extraes factor común en el primer miembro, cancelas términos opuestos en el segundo miembro, y queda:
(M1 + M2)*T = 0, divides por (M1 + M2) en ambos miembros, y queda:
T = 0;
luego, reemplazas este valor remarcado en las ecuaciones señaladas (1) (3), cancelas términos nulos, y luego en ambas ecuaciones despejas:
a = -g*senθ, reemplazas datos, y queda:
a = 9,8*sen(30°), resuelves el segundo miembro, y queda:
a = -4,9 m/s2.
Luego, puedes concluir que la tensión de la cuerda es nula, y que la aceleración tiene dirección paralela a la rampa, con sentido hacia abajo, y que su módulo es 4,9 m/s2.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 13/12/19Vamos con una orientación.
Considera un sistema de referencia con sentido de giro positivo horario.
Luego, tienes los datos de la rueda más pequeña:
RA = 20 cm = 0,2 m (radio),
tAi = 0 (instante inicial),
θAi = 0 (posición angular inicial),
fAi = 120 rev/min = 120/60 = 2 rev/s (frecuencia inicial de rotación), de donde tienes:
ωAi = 2π*fAi = 2π*2 = 4π rad/s (rapidez angular inicial),
ωAf = 0 (rapidez angular final),
tAf = 16 s (instante final);
luego, planteas la expresión de la aceleración angular de Movimiento Circular Uniformemente Variado, y queda:
αA = (ωAf - ωAi)/(tAf - tAi) = (0 - 4π)/(16 - 0) = -4π/16 = -π/4 rad/s2;
luego, plantas las expresiones de la función posición angular y de la función velocidad angular (observa que el instante inicial es igual a cero), y queda:
θA(t) = θAi + ωAi*t + (1/2)*αA*t2,
ωA(t) = ωAi + αA*t,
reemplazas valores, cancelas términos nulos, resuelves coeficientes, y queda:
θA(t) = 4π*t - (π/8)*t2 (1),
ωA(t) = 4π - (π/4)*t (2).
Luego, tienes los datos de la rueda más grande:
RB = 40 cm = 0,4 m (radio),
tBi = 0 (instante inicial),
θBi = 0 (posición angular inicial),
fBi = 240 rev/min = 240/60 = 4 rev/s (frecuencia inicial de rotación), de donde tienes:
ωBi = 2π*fBi = 2π*4 = 8π rad/s (rapidez angular inicial),
ωBf = 0 (rapidez angular final),
tBf = 8 s (instante final);
luego, planteas la expresión de la aceleración angular de Movimiento Circular Uniformemente Variado, y queda:
αB = (ωBf - ωBi)/(tBf - tBi) = (0 - 8π)/(8 - 0) = -8π/8 = -π rad/s2;
luego, plantas las expresiones de la función posición angular y de la función velocidad angular (observa que el instante inicial es igual a cero), y queda:
θB(t) = θBi + ωBi*t + (1/2)*αB*t2,
ωB(t) = ωBi + αB*t,
reemplazas valores, cancelas términos nulos, resuelves coeficientes, y queda:
θB(t) = 8π*t - (π/2)*t2 (3),
ωB(t) = 8π - π*t (4).
a)
Ya tienes remarcadas las expresiones correspondientes.
b)
Planteas la condición de velocidades angulares iguales, y queda la ecuación:
ωA(t) = ωB(t), sustituyes las expresiones señaladas (2) (4), y queda:
4π - (π/4)*t = 8π - π*t, multiplicas por 4 y divides por π en todos los términos, y queda:
16 - t = 32 - 4*t, y de aquí despejas:
t = 16/3 s ≅ 5,333 s,
que es el instante en el cuál las dos ruedas tienen velocidades angulares iguales.
Planteas la condición de rapideces lineales iguales para puntos periféricos de ambas ruedas, y queda:
vA(t) = vB(t),
sustituyes las expresiones de las rapideces lineales en función de las velocidades angulares y de los radios de las ruedas, y queda:
RA*ωA(t) = RB*ωB(t), reemplazas los valores de los radios, sustituyes las expresiones señaladas (2) (4), y queda:
0,2*(4π - (π/4)*t) = 0,4*(8π - π*t), divides por 0,2 en ambos miembros, y queda:
4π - (π/4)*t = 2*(8π - π*t), distribuyes en el segundo miembro, y queda:
4π - (π/4)*t = 16π - 2π*t, multiplicas por 4 y divides por π en todos los términos, y queda:
16 - t = 64 - 8*t, y de aquí despejas:
t = 48/7 s ≅ 6,857 s,
que es el instante en el cuál los puntos periféricos de ambas ruedas tienen rapideces lineales iguales.
c)
Luego, tienes las expresiones señaladas (1) (3), que corresponden a las funciones de posición de las ruedas, por lo que queda que evalúes dichas expresiones en los instantes que tienes remarcados en el inciso anterior.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Me podrían corregir el siguiente ejercicio por favor?
Un avión de juguete de masa 0'15kg pende de un hilo de 0'5m. El avión lleva un pequeño motor que lo pone en movimiento. Cuando el motor se pone en marcha, describe una trayectoria circular de radio 0'3m. Determinar el módulo de la velocidad del avión.
he aquí lo que yo he hecho:


Antonio Silvio Palmitano
el 13/12/19Observa que tienes los datos para plantear el valor del seno del ángulo que determina la dirección del hilo con la vertical, ya que los datos que tienes son la longitud de la hipotenusa y la longitud del cateto opuesto al ángulo, que tienes señalados en el triángulo rectángulo de tu diagrama, por lo que debes plantear:
senθ = R/L = 0,3/0,5 = 0,6,
de donde tienes:
cosθ = √(1 - sen2θ) = √(1 - 0,62) = √(1 - 0,36) = √(0,64) = 0,8.
Luego, has planteado correctamente el diagrama de fuerzas, y el sistema de ecuaciones correspondiente, de acuerdo con la Segunda Ley de Newton:
T*senθ = M*aR, de aquí despejas: aR = T*senθ/M (1),
T*cosθ - M*g = 0, de aquí despejas: T = M*g/cosθ = 0,15*9,8/0,8 = 1,8375 N, que es el módulo de la tensión del hilo;
luego, reemplaza el valor remarcado y los demás datos en la ecuación señalada (1), y queda:
aR = 1,8375*0,6/0,15 = 7,35 m/s2, que es el módulo de la aceleración radial del avión;
luego, planteas la expresión del módulo de la aceleración radial del avión, en función de su rapidez lineal y del radio de giro, y queda:
aR = v2/R, y de aquí despejas:
v = √(R*aR) = √(0,3*7,35) = √(2,205) m/s ≅ 1,485 m/s, que es el valor de la rapidez lineal del avión.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/12/194)
Tienes que el motor funciona seis horas diarias durante treinta días, por lo que su intervalo de tiempo funcionando es:
Δt = 6*30 = 180 h.
Luego, planteas la expresión del costo total de la energía que se suministró al motor (Ct = 600 S), en función del precio unitario (pu = 0,50 S/KW*h), y de la energía suministrada (U), y queda:
Ct = pu*U, y de aquí despejas:
U = Ct/pu = 600/0,5 = 1200 KW*h.
Luego, planteas la expresión de la potencia del motor en función de la energía suministrada y del intervalo de tiempo de funcionamiento, y queda:
Pot = U/Δt = 1200/180 = 20/3 KW ≅ 6,667 KW.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 12/12/195)
c)
Tienes los datos de la situación inicial:
Vi = 12 V (diferencia de potencial),
Ii = 3 A (intensidad de corriente);
luego, planteas la expresión de la resistencia en función de la diferencia de potencial y de la intensidad de corriente, de acuerdo con la Ley de Ohm, y queda:
R = Vi/Ii = 12/3 = 4 Ω.
a)
Planteas la expresión de la intensidad de corriente en función de la diferencia de potencial y de la resistencia, de acuerdo con la Ley de Ohm, y queda:
Ia = Va/R = 120/4 = 30 A.
b)
Planteas la expresión de la diferencia de potencial en función de la intensidad de corriente y de la resistencia, de acuerdo con la Ley de Ohm, y queda:
Vb = R*Ib = 4*0,2 = 0,8 V.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/12/192)
Por favor envía foto de la figura a la que refiere tu enunciado para que podamos ayudarte.
3)
Vamos con una orientación.
Planteas la expresión de la resistencia de la barra de aluminio en función de la resistividad del Aluminio, de la longitud de la barra y del área de su sección transversal, y queda:
Rb(Al) = ρAl*Lb(Al)/Ab(Al) (1);
luego, planteas la expresión del área de la sección transversal de la barra de aluminio en función de su diámetro (observa que es circular), y queda:
Ab(Al) = π*db(Al)2/4 (2).
Planteas la expresión de la resistencia de la barra de cobre en función de la resistividad del Cobre, de la longitud de la barra y del área de su sección transversal, y queda:
Rb(Cu) = ρCu*Lb(Cu)/Ab(Cu) (3);
luego, planteas la expresión del área de la sección transversal de la barra de cobre (observa que es cuadrada) en función de su lado, y queda:
Ab(Al) = Lb(Cu)2 (4).
Luego, tienes en tu enunciado la relación entre las longitudes de las barras:
Lb(Cu) = (1/2)*Lb(Al) (5).
Luego, tienes en tu enunciado la relación entre las resistencias de las barras:
Rb(Cu) = 2*Rb(Al) (6).
Luego, tienes los datos:
db(Al) = 5 cm = 5*10-2 m (diámetro de la barra de aluminio),
ρAl = 2,82*10-8 Ω*m (resistividad del aluminio),
ρCu = 1,7*10-8 Ω*m (resistividad del cobre);
luego, tienes que reemplazar datos en todas las ecuaciones numeradas, y resolver el sistema de ecuaciones.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola muy buenas. Estoy preparándome la prueba de acceso para mayores de 25 años para la universidad, y debo prepararme la fase específica de física, pero en el centro de estudios al que voy no dan esa materia, y me está costando bastante encontrar buenas formas de estudio. He visto que hay algunos libros por internet, los cuales no me puedo permitir ahora mismo, pero posiblemente lo haga en unas semanas. Me gustaría saber si hay algún portal de estudios gratuito del que poder ayudarme, o saber si alguien me puede pasar pdf de los libros preparatorios u orientarme un poco.
Un saludo y gracias!


Raúl RC
el 11/12/19De lo que vas a disponer aquí es de multitud de videos ordenados por los bloques que forman parte del temario de las pruebas PAU, totalmente gratuitos.
También te digo que puedes suscribirte por un módico precio a los planes pro de la web, los cuales podrán proporcionarte multitud de material en forma de pdf, etc.
Envia un email a unicoos@unicoos.com