-


Antonio Silvio Palmitano
el 6/12/19Observa que a partir de los valores de las masas de los bloques, tienes que el bloque apoyado sobre la superficie horizontal se desplaza hacia la derecha según tu figura, y también tienes que el bloque de la izquierda asciende y que el bloque de la derecha desciende, y observa además que los desplazamientos de los bloques tienen módulos iguales, al igual que sus velocidades, y que sus aceleraciones.
Luego, observa que sobre el bloque colgante de la izquierda están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Tensión de la cuerda: T12, hacia arriba,
Peso: P1 = M1*g, hacia abajo;
luego, establece un sistema de referencia con eje OY vertical con sentido positivo hacia arriba, aplicas la Segunda Ley de Newton, y queda la ecuación (observa que sustituimos las expresiones de los módulos de las fuerzas):
T12 - M1*g = M1*a, y de aquí despejas: T12 = M1*g + M1*a (1).
Luego, observa que sobre el bloque apoyado en la superficie horizontal están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Tensión de la cuerda de la derecha: T23, horizontal, hacia la derecha,
Tensión de la cuerda de la izquierda: T12, horizontal, hacia la izquierda,
Peso: P2 = M2*g, vertical, hacia abajo,
Acción normal de la superficie de apoyo: N2, vertical, hacia arriba;
luego, establece un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
T23 - T12 = M2*a (2a),
N2 - M2*g = 0, y de aquí despejas: N2 = M2*g, que es la expresión del módulo de la acción normal de la superficie de apoyo.
Luego, observa que sobre el bloque colgante de la derecha están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Tensión de la cuerda: T23, hacia arriba,
Peso: P3 = M3*g, hacia abajo;
luego, establece un sistema de referencia con eje OY vertical con sentido positivo hacia abajo, aplicas la Segunda Ley de Newton, y queda la ecuación (observa que sustituimos las expresiones de los módulos de las fuerzas):
M3*g - T23 = M3*a, y de aquí despejas: T23 = M3*g - M3*a (3).
Luego, sustituyes las expresiones señaladas (1) (3) en la ecuación señalada (2a), y queda:
M3*g - M3*a - (M1*g + M1*a) = M2*a, y de aquí despejas: a = (M3 - M1)*g/(M1 + M2 + M3), que es la expresión del módulo de la aceleración de los bloques;
luego, sustituyes esta última expresión remarcada en las ecuaciones señaladas (1) (3), y queda:
T12 = M1*g + M1*(M3 - M1)*g/(M1 + M2 + M3) = M1*g*[1 + (M3 - M1)/(M1 + M2 + M3)],
que es una expresión del módulo de la tensión de la cuerda de la izquierda,
T23 = M3*g - M3*(M3 - M1)*g/(M1 + M2 + M3) = M3*g*[1 - (M3 - M1)/(M1 + M2 + M3)],
que es una expresión del módulo de la tensión de la cuerda de la derecha.
Luego, planteas las expresiones de los módulos, direcciones, sentidos y puntos de aplicación de las reacciones de las fuerzas aplicadas sobre cada bloque, y queda:
Para el bloque colgante de la izquierda:
Reacción a la tensión de la cuerda: T12, vertical, hacia abajo, aplicada en el punto de amarre de este bloque con la cuerda,
Reacción al peso: P1 = M1*g, vertical, hacia arriba, aplicada en el centro de la Tierra (observa que la dirección, en realidad, es radial).
Para el bloque apoyado en la superficie horizontal:
Reacción a la tensión de la cuerda de la derecha: T23, horizontal, hacia la izquierda, aplicada en el punto de amarre de este bloque con esta cuerda,
Reacción a la tensión de la cuerda de la izquierda: T12, horizontal, hacia la derecha, aplicada en el punto de amarre de este bloque con esta cuerda,
Reacción al peso: P2 = M2*g, vertical, hacia arriba, aplicada en el centro de la Tierra (observa que la dirección, en realidad, es radial),
Reacción normal sobre la superficie de apoyo: N2, vertical, hacia abajo, aplicada en la zona de contacto de este bloque sobre la superficie.
Para el bloque colgante de la derecha:
Reacción a la tensión de la cuerda: T23, vertical, hacia abajo, aplicada en el punto de amarre de este bloque con la cuerda,
Reacción al peso: P3 = M3*g, vertical, hacia arriba, aplicada en el centro de la Tierra (observa que la dirección, en realidad, es radial).
Espero haberte ayudado.
-
Hola. Tenía dudas respecto a cómo plantear este ejercicio. Las soluciones son Ec alfa = 2Ec protón y (R alfa/R protón) por raíz de 2.
Se aceleran una partícula alfa y un protón mediante una diferencia de potencial AV y penetran perpendicularmente en un campo magnético uniforme de intensidad B. Determina:
La relación existente entre las energías cinéticas con que entran la partícula alfa y el protón en el campo magnético.
La relación entre los radios de sus respectivas trayectorias.
Si pueden resolvérmelo se lo agradecería. Conozco las fórmulas pero no sé cómo empezar a plantear la relación.


Antonio Silvio Palmitano
el 6/12/19Planteas la ecuación trabajo de la fuerza eléctrica-variación de la energía cinética para cada partícula en su etapa de aceleración, y tienes las ecuaciones:
ECα = qα*ΔV,
ECp = qp*ΔV;
luego, divides miembro a miembro entre ambas ecuaciones, simplificas, y queda:
ECα/ECp = qα/qp, reemplazas los valores de las cargas de las partículas (designamos con e al valor de la carga elemental), y queda:
ECα/ECp = 2e/e, simplificas, y queda:
ECα/ECp = 2, y de aquí despejas:
ECα = 2*ECp.
Luego, sustituyes las expresiones de las energías cinéticas de las partículas en esta última ecuación remarcada, y queda:
(1/2)*Mα*vα2 = 2*(1/2)*Mp*vp2, y de aquí despejas:
vp2/vα2 = Mα/(2*Mp), sustituyes la expresión de la masa de la partícula α (consideramos: Mα ≅ 4*Mp), simplificas el segundo miembro, y queda:
vp2/vα2 = 2 (1).
Luego, para la etapa de giro, aplicas las Segunda Ley de Newton para cada partícula, y quedan las ecuaciones:
qp*vp*B = Mp*acp,
qα*vα*B = Mα*acα,
sustituyes las expresiones de la carga y de la masa de la partícula α, y queda:
qp*vp*B = Mp*acp,
2*qp*vα*B = 4*Mp*acα,
divides miembro, simplificas, y queda:
vp/(2*vα) = acp/(4*acα), multiplicas por 4 en ambos miembros, y queda:
2*vp/vα = acp/acα;
luego, sustituyes las expresiones de los módulos de las aceleraciones centrípetas en función de las rapideces lineales y de los radios de las trayectorias, y queda:
2*vp/vα = (vp2/Rp)/(vα2/Rα), multiplicas por vα/vp en ambos miembros, y queda:
2 = (vp/Rp)/(vα/Rα), resuelves el segundo miembro, asocias factores y divisores semejantes, y queda:
2 = (vp/vα)*(Rα/Rp), multiplicas por Rp/Rα en ambos miembros, y luego despejas:
vp/vα = 2*Rp/Rα, elevas al cuadrado en ambos miembros, distribuyes potencias en ambos miembros, y queda:
vp2/vα2 = 4*Rp2/Rα2 (2).
Luego, sustituyes la expresión señalada (2) en el primer miembro de la ecuación señalada (1), y queda:
4*Rp2/Rα2 = 2, divides por 2 y multiplicas por Rα2 en ambos miembros, y luego despejas:
Rα2 = 2*Rp2, extraes raíz cuadrada positiva en ambos miembros, distribuyes la raíz y simplificas en el segundo miembro, y queda:
Rα = √(2)*Rp.
Espero haberte ayudado.
-
ola, alguien me podria exolicar las fuerzas de friccion cinetica y estática. estaba intentando este ejercicio

yo he intentado resolverlo asi

pero resulta que mis resultados no se corresponden para nada con los que deberian dar
Usuario eliminado
el 4/12/19Las fuerzas que actúan en el eje Y son: hacia abajo el peso, y hacia arriba la componente Y de la tensión T, de valor T·sen 45, de manera que la reacción normal del plano sobre el cuerpo es m·g - T·sen 45. Esto afecta al cálculo de la fuerza de rozamiento.
a)
T
· cos 45 – μ(est)
· (m · g – T · sen 45) = 0
Igualando
a 0 calculamos el valor de la fuerza a partir del cual se iniciará
el movimiento.
Sustituyendo
los datos conocidos obtenemos
T
= 362 N (aprox.)
b)
Una
vez iniciado el movimiento, el coeficiente de rozamiento es menor,
con lo que hay que disminuir la tensión para que el movimiento no
sea acelerado. Si queremos que sea uniforma, la resultante ha de ser
nula:
T
· cos 45 – μ(cin)
· (m · g – T · sen 45) = 0
Sustituyendo
los datos conocidos obtenemos
T
= 339,5 (aprox.)
c)
Para
T = 100 N, el cuerpo obviamente no se mueve, pues ya se vio que para
que se inicie el movimiento la T ha de valer, como mínimo, 362 N.
La
fuerza de rozamiento, entonces, tiene que ser igual a la componente
horizontal de la tensión
F(roz)
= T · cos 45 = 100 · 0,707 = 70,7 N
La
normal será, en este caso,
N
= m · g – F · sen 45 = 55 · g – 100 · 0,707
N
= 468,3 N (aprox)
-
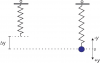
. Un resorte se encuentra suspendido del punto o de un soporte fijo tal como indica la figura 1. Después de que al extremo libre del resorte se le conecta un cuerpo de masa 2.00 kg, el resorte se estira ∆y = 0.10 m y el cuerpo queda en equilibrio. Luego, el cuerpo se pone a oscilar verticalmente al dársele una velocidad inicial hacia abajo igual a 0.10 m/s. Una vez en movimiento, sobre el cuerpo actúa una fuerza de rozamiento F proporcional a su velocidad instantánea v e igual a F = −8.00v, expresión escrita en el sistema internacional de unidades.
El periodo de las oscilaciones amortiguadas del cuerpo es:


Antonio Silvio Palmitano
el 4/12/19Vamos con una orientación.
Establece un sistema de referencia con eje OY vertical con sentido positivo hacia arriba.
Luego, observa que sobre el cuerpo en reposo están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Fuerza elástica del resorte: |Fe| = k*Δyi, hacia arriba;
Peso: |P| = M*g, hacia abajo;
luego, aplicas la Primera Ley de Newton, y queda la ecuación:
|Fe| - |P| = 0, sustituyes las expresiones de los módulos de las fuerzas, y queda:
k*Δyi - M*g = 0, y de aquí despejas:
k = M*g/Δyi, reemplazas valores, y queda:
k = 2*9,8/0,1 = 196 N/m, que es el valor de la constante elástica del resorte.
Luego, observa que sobre el cuerpo en movimiento están aplicadas tres fuerza verticales, de las que indicamos sus expresiones vectoriales (observa que indicamos en negrita a las expresiones vectoriales):
Peso: P = M*g (observa que su sentido es hacia abajo),
Fuerza elástica del resorte: Fe = -k*y (observa que la posición del cuerpo toma valores negativos, por lo que el sentido de la fuerza es hacia arriba),
Rozamiento dinámico: frd = -800*v (observa que la velocidad es hacia abajo, por lo que el sentido de esta fuerza es hacia arriba.
Luego, aplicas la Segunda Ley de Newton, y queda la ecuación vectorial:
P + Fe + frd = M*a, sustituyes las expresiones vectoriales de las fuerzas, y queda:
M*g - k*y - 800*v = M*a, restas M*a y restas M*g en ambos miembros, y queda:
-M*a - k*y - 800*v = -M*g, multiplicas por -1 y divides por M en todos los términos, y queda:
a + (k/M)*y + (800/M)*v = g, reemplazas valores numéricos (k = 196 N/m, M = 2 Kg), resuelves coeficientes, y queda:
a + 98*y + 400*v = g, ordenas términos en el primer miembro, y queda:
a + 400*v + 98*y = g, sustituyes las expresiones de la aceleración y de la velocidad en función de la posición y del tiempo, y queda:
d2y/dt2 + 400*dy/dt + 98*y = g,
que es la ecuación diferencial vectorial que corresponde al movimiento del cuerpo;
luego, como la dirección de movimiento del cuerpo es rectilínea (observa que es la dirección del eje OY), puedes prescindir de las consideraciones vectoriales, reemplazas el valor que corresponde a la aceleración gravitatoria terrestre (observa que su sentido es hacia abajo), y queda:
d2y/dt2 + 400*dy/dt + 98*y = -9,8,
y solo queda que resuelvas esta ecuación diferencial lineal, de segundo orden, de primer grado, no homogénea, y con coeficientes constantes,
con las condiciones iniciales que tienes en tu enunciado:
y(0) = 0 (posición inicial del cuerpo),
(dy/dt)(0) = -10 m/s (velocidad inicial del cuerpo).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Una masa pequeña m=2.7 kg está atada de una cuerda de longitud 7.5 m cuyo extremo opuesto está fijo. Si la
masa se suelta desde la posición horizontal con una velocidad 2.7 m/s, ¿cuál es la tensión en la cuerda cuando
llega a la posición vertical?

Antonio Silvio Palmitano
el 4/12/19Considera un sistema de referencia con origen de coordenadas en el punto más bajo que alcanza el objeto, con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba.
Luego, observa que cuando el objeto pasa por el origen de coordenadas, tienes que sobre él están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Tensión de la cuerda: T, hacia arriba;
Peso: P = M*g, hacia abajo.
Luego, aplicas la Segunda Ley de Newton (observa que el cuerpo "gira" alrededor de un eje que pasa por el punto fijo de la cuerda), y queda la ecuación:
T - M*g = M*acp,
sustituyes la expresión del módulo de la aceleración centrípeta en función del módulo de la velocidad lineal instantánea y del radio de giro (observa que es igual a la longitud de la cuerda), y queda:
T - M*g = M*v2/L, y de aquí despejas:
T = M*g + M*v2/L (1).
Luego, planteas la expresión de la energía mecánica inicial del objeto (observa que su velocidad inicial es nula, por lo que solo tiene energía potencial gravitatoria en este punto, y que la componente vertical de su posición inicial es: yi = L), y queda:
EMi = EPi, sustituyes la expresión de la energía potencial inicial, y queda:
EMi = M*g*L (2).
Luego, planteas la expresión de la energía mecánica final del objeto (observa que la componente vertical de su posición final es: yf = 0, por lo que solo tiene energía cinética de traslación en este punto), y queda:
EMf = ECf, sustituyes la expresión de la energía cinética final, y queda:
EMf = (1/2)*M*v2 (3).
Luego, si desprecias todo tipo de rozamiento, planteas conservación de la energía mecánica entre la situación final y la inicial, y queda la ecuación:
EMf = EMi, sustituyes las expresiones señaladas (3) (2), y queda:
(1/2)*M*v2 = M*g*L, y de aquí despejas:
v2 = 2*g*L (4).
Luego, sustituyes la expresión señalada (4) en el numerador del último término de la ecuación señalada (1), simplificas, y queda:
T = M*g + 2*M*g, resuelves, y queda:
T = 3*M*g,
y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Una pelota de masa m=6.9 kg es arrojada horizontalmente con una velocidad 29.3 m/s contra una cuña de masa
M= 15.9 kg en forma de plano inclinado, que tiene un ángulo (y)° respecto a la horizontal. Luego del choque, elplano inclinado se desliza sobre la superficie horizontal sobre la que descansa y la pelota rebota verticalmente
hacia arriba. Considerando el choque como una colisión elástica, ¿cuál es la velocidad de la pelota después del
choque? -
Ola alguien sería tan amable de explicarme las fuerzas de rozamiento estatica y cinética? Estaba resolviendo este ejercicio

aquí lo que yo he hecho
lo que ocurre es que no me dan para nada las soluciones que deberían dar y no sé que tengo mal
he aquí las supuestas soluciones
a)T=361N b)T=338N c) Froz=70,7N (esto si que me da sorprendentemente) y N=468'28N
ayuda por favor


Raúl RC
el 8/12/19Te dejo un vídeo que grabó el profe hace un tiempo sobre estos coeficientes. Seguro que te sirve para acabar de resolver tu ejercicio. Si aun así sigues teniendo dudas, nos escribes de nuevo ;)
https://www.youtube.com/watch?v=g76qlR5WayI
-
Tengo problema con un crucigrama de física 😖 espero y me puedan ayudar
Estableció su pricipio enfocado en una jaula (7letras)
Material que permite la electricidad (9letras)
El mejor conductor de electricidad (3letras)
Primer científico de la electricidad (13 letras)
Camino por dónde pasa la electricidad (8letras)
Tipo de circuito no continuo (8letras)
Unidad de medida de las cargas (7 letras)
-
Tengo varios problemas similares, me podrían ayudar?
Una cubeta, de masa m = 60kg, sube partiendo del reposo; en 10s recorre una distancia de
5m.
a) Obtenga la velocidad y aceleración de la cubeta.
b) Obtenga la fuerza de la tensión en la cuerda.
c) Si la cubeta desciende, ¿qué tensión debería tener ahora la cuerda para conservar la misma
aceleración? Considere el cambio de signo que tendrá la aceleración.


Raúl RC
el 3/12/19Te recomiendo apliques la teoría que el profe explicó en este vídeo
https://www.youtube.com/watch?v=qnkmtfya9yM
-


Raúl RC
el 3/12/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos....