-
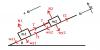
Me piden calcular h sabiendo que la masa de la bala es m y la del bloque M y la bala lleva una velocidad v. Si me podríais ayudar. Gracias.


Antonio Silvio Palmitano
el 28/10/19Establece un sistema de referencia con origen de coordenadas en la posición inicial del bloque, con eje OX horizontal con sentido positivo acorde al desplazamiento de la bala antes de chocar con el bloque, y con eje OY vertical con sentido positivo hacia arriba.
Luego, planteas las expresiones de las componentes del impulso del sistema masa-bloque antes del choque, y queda:
pAx = Mb*vAbx + MB*vABx = Mb*v + MB*0 = Mb*v + 0 = Mb*v,
pAy = Mb*vAby + MB*vABy = Mb*0 + MB*0 = 0 + 0 = 0.
Luego, planteas las expresiones de las componentes del impulso del sistema masa-bloque inmediatamente después del choque, y queda:
pDx = (Mb + MB)*vDx,
pDy = (Mb + MB)*vDy = (Mb + MB)*0 = 0.
Luego, como no actúan fuerzas externas en el plano de movimiento del sistema durante el choque, planteas conservación del impulso, y queda el sistema de ecuaciones:
pDx = pAx,
pDy = pAy,
sustituyes expresiones, y queda:
(Mb + MB)*vDx = Mb*v, y de aquí despejas: vDx = Mb*v/(Mb + MB) (1),
0 = 0, que es una identidad verdadera.
Luego, planteas la expresión de la energía mecánica del sistema inmediatamente después del choque (observa que es solo energía cinética de traslación), y queda:
EMD = (1/2)*(Mb + MB)*vDx2, sustituyes la expresión señalada (1) elevada al cuadrado, y queda:
EMD = (1/2)*(Mb + MB)*Mb2*v2/(Mb + MB)2, simplificas, y queda:
EMD = (1/2)*Mb2*v2/(Mb + MB) (2).
Luego, planteas la expresión de la energía mecánica final del sistema (observa que es solo energía potencial gravitatoria), y queda:
EMf = (Mb + MB)*g*h (3).
Luego, si se desprecia todo tipo de rozamiento, planteas conservación de la energía mecánica del sistema, y queda la ecuación:
EMf = EMD, sustituyes las expresiones señaladas (3) (2), y queda:
(Mb + MB)*g*h = (1/2)*Mb2*v2/(Mb + MB), divides por (Mb + MB) y divides por g en ambos miembros, y queda:
h = (1/2)*Mb2*v2/[(Mb + MB)2*g],
que es la expresión de la altura máxima que alcanza el sistema en función de la masa de la bala, de la rapidez de la bala antes de chocar con el bloque, de la masa del bloque, y del módulo de la aceleración gravitatoria terrestre.
Espero haberte ayudado.
-
 Alguien me da una mano con este tema?? No recuerdo nada jaja, no pido que me lo resuelvan pero una breve explicación de cómo se plantean estos ejercicios
Alguien me da una mano con este tema?? No recuerdo nada jaja, no pido que me lo resuelvan pero una breve explicación de cómo se plantean estos ejercicios 

Breaking Vlad
el 28/10/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 28/10/19se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Francisco Javier
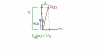
el 28/10/19Lo primero que debemos hacer es un diagrama de cuerpo libre donde se muestren las fuerzas que actúan en las dos masas.
Te dejo un bosquejo de dicho diagrama al final de la respuesta.
Vemos la presencia de las siguientes fuerzas:
Tensión de cuerda "T", fricción "ƒ", componente del peso horizontal "wx", componente del peso vertical "wy" y la normal "N".
Definamos algunas de estas fuerzas.
La fricción se halla aplicando la siguiente ecuación:
ƒ = µk*N
Donde "μk" es el coeficiente de fricción cinético y "N" es la normal.
Para un plano inclinado, con angulo "θ" respecto al suelo, siempre se cumple que:
wx = w*Sin(θ)
wy = w*Cos(θ)
Donde "w" es el peso. Conociendo que:
w = m*g
Tendremos que:
wx = m*g*Sin(θ)
wy = m*g*Cos(θ)
La fuerza normal siempre va perpendicular al plano.
Fíjate que el movimiento es solamente en el eje paralelo al plano. Según nuestro plano, este eje sera el "x".
Por ser en este eje donde hay movimiento, toda sumatoria de fuerzas sera igual a masa por aceleración (2da ley de newton).
En el eje perpendicular no hay movimiento. Según nuestro plano, este eje sera el "y".
Como no hay movimiento en este eje, toda sumatoria de fuerzas sera igual a cero (1ra ley de newton).
Al escribir las ecuaciones, debemos respetar el sistema establecido en nuestro diagrama.
La aceleración "a" sera igual para ambas masas.
Dicho esto podemos empezar a escribir las ecuaciones.
Para la masa dos:
Haciendo una sumatoria de fuerzas en el eje vertical "y":
∑Fy = 0
N2 - wy2 = 0
Reemplazando "wy2" por su expresión:
N2 - m2*g*Cos(θ) = 0
Despejando para "N2":
N2 = m2*g*Cos(θ)
Y desarrollando con los datos del problema:
N2 = 7.5*9.81*Cos(35º)
N2 = 60.2691 N
Haciendo una sumatoria de fuerzas en el eje horizontal "x":
∑Fx = m2*a
- ƒ2 + T + wx2 = m2*a
Reemplazando "ƒ2" y "wx2" por su expresión:
- µk2*N2 + T + m2*g*Sin(θ) = m2*a
Despejando para "T":
T = m2*a + µk2*N2 - m2*g*Sin(θ)
Y desarrollando con los datos del problema:
T = 7.5*a + 0.2*60.2691 - 7.5*9.81*Sin(35º)
T = 7.5*a + 12.0538 - 42.2009
T = 7.5*a - 30.1471 [1]
Para la masa uno:
Haciendo una sumatoria de fuerzas en el eje vertical "y":
∑Fy = 0
N1 - wy1 = 0
Reemplazando "wy1" por su expresión:
N1 - m1*g*Cos(θ) = 0
Despejando para "N1":
N1 = m1*g*Cos(θ)
Y desarrollando con los datos del problema:
N1 = 5*9.81*Cos(35º)
N1 = 40.1794 N
Haciendo una sumatoria de fuerzas en el eje horizontal "x":
∑Fx = m1*a
- ƒ1 - T + wx1 = m1*a
Reemplazando "ƒ1" y "wx1" por su expresión:
- µk1*N1 - T + m1*g*Sin(θ) = m1*a
Reemplazamos también el valor de tensión (ecuación #1):
- µk1*N1 - (7.5*a - 30.1471) + m1*g*Sin(θ) = m1*a
- µk1*N1 - 7.5*a + 30.1471 + m1*g*Sin(θ) = m1*a
Despejando para "a":
m1*a + 7.5*a = - µk1*N1 + 30.1471 + m1*g*Sin(θ)
a*(m1 + 7.5) = - µk1*N1 + 30.1471 + m1*g*Sin(θ)
a = [- µk1*N1 + 30.1471 + m1*g*Sin(θ)]/(m1 + 7.5)
Y desarrollando con los datos del problema:
a = [- 0.15*40.1794 + 30.1471 + 5*9.81*Sin(35º)]/(5 + 7.5)
a = 4.1803 m/s2
Reemplazando este valor en la ecuación #1 y desarrollando terminamos el problema:
T = 7.5*a - 30.1471
T = 7.5*4.1803 - 30.1471
T = 1.2052 N
Bosquejo:
-
 La A es como lo hace mi profe, pero yo he usado el alzance para saber la v0 pero el tiempo no concuerda. Aquí dejo mi solución (B).
La A es como lo hace mi profe, pero yo he usado el alzance para saber la v0 pero el tiempo no concuerda. Aquí dejo mi solución (B).  Y el enunciado.
Y el enunciado.  MUCHAS GRACIAS!! En especial al profe Miguel de unicoos que me ha ayudado un montón
MUCHAS GRACIAS!! En especial al profe Miguel de unicoos que me ha ayudado un montón

Miguel Fuego
el 27/10/19Pues, aparentemente el error está en la parte de tu profe. Cuando está calculando el componente en 'x', por algún motivo, ha puesto '2t'. Si te fijas, tu solución es exactamente el doble de la suya, lo que se explica a partir de ese '2' misterioso que aparece.
¡Gracias a ti! No soy profe, pero me gusta echar una mano.
¡Mucha suerte mañana!
-


Francisco Javier
el 28/10/19Lo primero que debemos hacer es un diagrama de cuerpo libre donde se muestren las fuerzas que actúan sobre el objeto.
Te dejo un bosquejo de dicho diagrama al final de la respuesta.
a)
Para toda sumatoria que hagamos, debemos respetar el sistema asignado en el diagrama de cuerpo libre.
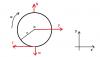
Si hacemos una sumatoria de momentos respecto al punto "o" igual al momento de inercia "I" por la aceleración angular "α":
∑M = I*α
La única fuerza que produce momento en "o" (la que hace girar el cilindro) es la fuerza de fricción.
Su brazo de palanca es igual al radio "r" del cilindro.
Para un cilindro solido, el momento de inercia en el centro de masa es igual a:
I = 0.5*M*r2
Donde "M" es la masa del cilindro y "r" su radio.
Dicho esto, escribimos la ecuación:
f*r = I*α
Despejando para "f":
f = I*α/r
Reemplazando "I" por su expresión:
f = 0.5*M*r2*α/r
f = 0.5*M*r*α [1]
Reemplazando datos del problema:
f = 0.5*50*0.5*α
f = 12.5*α
Haciendo una sumatoria de fuerzas horizontales igual a masa por aceleración (hay movimiento acelerado en este eje):
∑Fx = M*a
F - f = M*a [2]
Reemplazamos "f" por la expresión hallada:
F - 12.5*α = M*a
Y colocamos la aceleración angular en función de la aceleración lineal sabiendo que:
α = a/r
Dicho esto:
F - 12.5*(a/r) = M*a
Despejando para "a":
M*a + (12.5*a)/r = F
a*(M + 12.5/r) = F
a = F/(M + 12.5/r)
Reemplazando datos del problema y desarrollando:
a = 90/(50 + 12.5/0.5)
a = 1.2 m/s2
Por lo que la aceleración angular valdría:
α = a/r
α = 1.2/0.5
α = 2.4 rad/s2
b)
La fuerza máxima que se puede aplicar y que aun el cuerpo se mueva sin deslizar se halla sabiendo que:
f = µs*N
Donde "μs" es el coeficiente de fricción estático y "N" la normal.
Cuando la fricción adquiere este valor, la fuerza aplicada sera la máxima que podemos ejercer para que aun el cuerpo no deslice.
Para valores mayores a esta fuerza aplicada, el cilindro se deslizara.
Haciendo una sumatoria de fuerzas verticales igual a acero (no hay movimiento en este eje):
∑Fy = 0
N - w = 0
Despejando para "N":
N = w
Y como sabemos que:
w = M*g
Donde:
g = 9.81 m/s2
Hallamos que:
N = M*g
N = 50*9.81
N = 490.5 N
Por lo que la fuerza de fricción sera:
f = μs*N
f = 0.3*490.5
f = 147.15 N
Debemos calcular la aceleración angular y lineal para este caso.
Retomamos la ecuación #1:
f = 0.5*M*r*α
Despejamos para "α":
α = f/(0.5*M*r)
Reemplazando datos del problema y desarrollando:
α = 147.15/(0.5*50*0.5)
α = 11.772 rad/s2
Y como:
a = α*r
Reemplazamos y desarrollamos para la aceleración lineal:
a = 11.772*0.5
a = 5.886 m/s2
Teniendo este valor, volvemos a utilizar la ecuación #2:
F - f = M*a
Despejando para "F":
F = M*a + f
Reemplazando datos del problema y desarrollando:
F = 50*5.886 + 147.15
F = 441.45 N
c)
Como el valor de fuerza aplicada (500 N) es mayor que la fuerza máxima para que el cilindro deslice (441.45 N) cambian las cosas.
Ya no podemos decir que la aceleración angular es función de la aceleración lineal del cilindro.
Debemos calcular cada una de manera independiente.
Vamos primero con la aceleración angular.
Para hallarla hacemos sumatoria de momento en "o" igual al momento de inercia por la aceleración angular.
Similar a lo que hicimos en el inciso b).
Recurrimos nuevamente a la ecuación #1. Aquí lo que cambia es el valor de la fuerza de fricción.
Dada la fuerza aplicada, se tiene una fuerza de fricción cinética.
Entonces:
f = μk*N
Donde la normal tiene el mismo valor que en el inciso b).
Dicho esto:
f = 0.25*490.5
f = 122.625 N
Por lo que la aceleración angular seria:
f = 0.5*M*r*α
α = f/(0.5*M*r)
α = 122.625/(0.5*50*0.5)
α = 9.81 rad/s2
Para la aceleración lineal hacemos sumatoria de fuerzas horizontales igual a masa por aceleración.
Osea, aplicamos nuevamente la ecuación #2:
F - f = M*a
Despejando "a":
a = (F - f)/M
Reemplazando datos y desarrollando damos por concluido el problema:
a = (500 - 122.625)/50
a = 7.5475 m/s2
Bosquejo:
-