-
EJERCICIO ELECTROSTÁTICA
Se muestra en la figura un ensamble de 3 condensadores ,cargados mediante una batería de fuerza electromotriz "E" . Si la diferencia de potencial a traves del condensador C1 vale 4 voltios . ¿ cual es el valor de la fuerza electromotriz de la bateria?
c1 = 2 uf c2 = 6 uf C 3 = 8 uf
A mi sales como respuesta 8 voltios , estará bien
la opciones son :
a) 2 voltios b) 4 voltios c) 6 voltios D) 8 voltios E) 12 voltios
por favor ayúdame no se si estará bien , ayúdame con esta duda, por favor en que no estoy seguro si estar bien.
AQUÍ ESTA LA FIGURA

Antonio Silvio Palmitano
el 29/9/19Comienza por plantear la expresión de la capacidad equivalente a los dos condensadores conectados en paralelo, y queda:
Cp12 = C1 + C2 = 2 + 6 = 8 μF.
Luego, planteas la expresión de la capacidad equivalente a los tres condensadores (observa que tienes una serie), y queda:
Ce = C3*Cp12/(C3 + Cp12) = 8*8/(8 + 8) = 64/16 = 4 μF.
Luego, planteas la expresión de la carga del circuito en función de la fuerza electromotriz y de la capacidad equivalente, y queda:
q = Ce*E = 4*E (en μC).
Luego, observa que los condensadores señalados C3 y Cp12 tienen esta misma carga por estar conectados en serie, observa que tienes el valor de la diferencia de potencial para el primero de ellos:
V3 = 4 V,
y que la expresión de la diferencia de potencial para el segundo es:
Vp12 = q/Cp12 = q/8 (en V).
Luego, observa que la suma de las dos diferencias de potencial de los condensadores conectados en serie es igual a la fuerza electromotriz, por lo que puedes plantear la ecuación:
E = V3 + Vp12,
sustituyes expresiones, y queda:
E = 4 + q/8,
sustituyes la expresión de la carga que tienes remarcada en el numerador del último término, y queda:
E = 4 + 4*E/8, simplificas en el último término, y queda:
E = 4 + E/2, multiplicas por 2 en todos los términos, y queda:
2*E = 8 + E, restas E en ambos miembros, y queda:
E = 8 V,
por lo que puedes concluir que la opción señalada (D) es la respuesta correcta.
Espero haberte ayudado.
-
Ejercicio electrostática
Un condensador de placas paralelas y 1uf de capacidad es cargado con 8 * 10-6 C . Este condensador se conecta a un condensador de 3uf descargado según como se muestra en la figura, la carga que al final adquiere el condensador de 3uf sera:
a mi me sales 2x10-6 como respuesta ,estarán bien
la opciones son :
a) 8 x10-6 C B) 2 X10-6 C) 6 X 10-6 C D) 8/3(10-6 ) C E)4 X 10 -6 C
a mi sales un resultados que no se si estarán bien , me puede ayuda si estar bien o no mi respuestaPor favor ayúdame


Antonio Silvio Palmitano
el 29/9/19Observa que tienes el valor de la carga inicial del primer condensador: q = 8*10-6 C,
y que al conectarlo con el segundo condensador, tienes que esta carga se redistribuye entre ambos dispositivos, por lo que puedes plantear que la suma de sus cargas es igual a la carga inicial, y queda la ecuación:
Q1 + Q2 = q, reemplazas el valor de la carga inicial, y queda:
Q1 + Q2 = 8*10-6 (*) (en C);
luego, planteas la expresión de la capacidad equivalente (observa que tienes que están conectados en paralelo, ya que las placas cargadas con el mismo signo están conectadas), y tienes la ecuación:
C = 1 + 3 = 4 μF = 4*10-6 F;
luego, planteas la expresión de la diferencia de potencial entre las placas de ambos condensadores (recuerda que están conectados en paralelo), en función de la capacidad equivalente (C) y de la carga total (Q1 + Q2), y queda:
V = (Q1 + Q2)/C = 8*10-6/(4*10-6) = 2 V.
Luego, planteas las expresiones de las cargas de los condensadores en función de sus capacidades y de su diferencia de potencial, y queda:
Q1 = C1*V = 1*10-6*2 = 2*10-6 C,
Q2 = C2*V = 3*2 = 6*10-6 C,
y puedes verificar que estos dos valores verifican la ecuación señalada (*),
por lo que puedes concluir que la opción señalada (C) es la respuesta correcta.
Espero haberte ayudado.
-
Buenas tardes , necesito ayuda en este problema, estoy en parciales
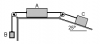 Los tres bloques de la
Fig están conectados por medio de cuerdas ligeras que pasan por poleas sin
fricción y se encuentran en reposo. Las masas de los bloques A y C son de 5 Kg
y 8 Kg, respectivamente, y las superficies de apoyo son lisas, Determinar: a)
la masa del bloque B, y b) la tensión en cada una de las cuerdas
Los tres bloques de la
Fig están conectados por medio de cuerdas ligeras que pasan por poleas sin
fricción y se encuentran en reposo. Las masas de los bloques A y C son de 5 Kg
y 8 Kg, respectivamente, y las superficies de apoyo son lisas, Determinar: a)
la masa del bloque B, y b) la tensión en cada una de las cuerdas

Francisco Javier
el 29/9/19Empezamos haciendo una sumatoria de fuerzas en el eje "x" de la masa "C" igual a cero (debido a que hay equilibrio).
Esta ultima aclaración ya no la repetiré para las demás sumatorias en las demás masas.
Respetando el sentido otorgado en el diagrama, nos quedaría:
∑Fx = 0
wC*Sin(25º) - T1 = 0
La expresión "wC*Sin(25º)" sale de la descomposición del peso de esta masa en el eje "x".
Sabiendo ademas que:
w = m*g
Tenemos que:
mC*g*Sin(25º) - T1 = 0
Despejando "T1":
T1 = mC*g*Sin(25º)
T1 = 8*9.81*Sin(25º)
T1 = 33.1671 N
Ahora hacemos una sumatoria de fuerzas en el eje "x" para la masa "A" igual a cero.
Respetando el sentido otorgado en el diagrama, nos quedaría:
∑Fx = 0
T1 - T2 = 0
33.1671 - T2 = 0
Despejando "T2":
T2 = 33.1671 N
Finalmente, hacemos sumatoria de fuerzas en el eje "y" para la masa "B" igual a cero.
Respetando el sentido otorgado en el diagrama, nos quedaría:
∑Fy = 0
T2 - wB = 0
33.1671 - wB = 0
Aplicando la definición de peso hecha arriba:
33.1671 - mB*g = 0
Despejando "mB":
mB*g = 33.1671
mB = 33.1671/g = 33.1671/9.81
mB = 3.3809 kg
Diagrama:
-
Buenos días, necesito ayuda con un problema de tiro parabólico, no se como hacerlo, en la solución dice que es un angulo de 75,96º. Muchas gracias por la ayuda de antemano.
Un cañón dispara balas con una velocidad de módulo indeterminado v0, actuando a partir de ese instante sobre ellas la aceleración constante de la gravedad de módulo indeterminado g. ¿Con qué ángulo θ hay que colocar el cañón respecto a la horizontal para que la altura máxima H alcanzada por las balas sea igual a su alcance D?


Francisco Javier
el 29/9/19Planteamos la ecuación de posición vertical de la bala:
y = yo + voy*t - 0.5*g*t2
Derivamos respecto al tiempo esta expresión para hallar la ecuación de velocidad vertical de la bala:
vy = d/dt [y] = voy - g*t
De esta expresión, cuando vy = 0, el tiempo pasa a ser el tiempo de subida:
vy = 0 → t = tsubida
Dicho esto:
0 = voy - g*tsubida
Despejando para "tsubida":
g*tsubida = voy
tsubida = voy/g
Si reemplazamos t = tsubida en la ecuación de posición vertical, y = ymax.
Entonces:
ymax. = yo + voy*tsubida - 0.5*g*tsubida2
ymax. = yo + voy*(voy/g) - 0.5*g*(voy/g)2
ymax. = yo + voy2/g - 0.5*g*(voy2/g2)
ymax. = yo + voy2/g - (0.5*voy2)/g
ymax. = yo + (0.5*voy2)/g
Planteamos ahora la ecuación de posición vertical de la bala:
x = xo + vox*t
Si la bala se dispara y vuelve al mismo plano paralelo del que fue lanzado, el tiempo de vuelo sera dos veces el tiempo de subida:
tvuelo = 2*tsubida
Si reemplazamos t = tvuelo en la ecuación de posición horizontal, x = xmax.
Entonces:
xmax. = xo + vox*tvuelo
xmax. = xo + vox*(2*voy/g)
xmax. = xo + (2*vox*voy)/g
Aplicamos la condición para que la altura máxima sea igual al alcance máximo:
ymax. = xmax.
yo + (0.5*voy2)/g = xo + (2*vox*voy)/g
Si tomamos como referencia el lugar justo donde se lanza la bala, xo = 0 e yo = 0.
Por lo que:
(0.5*voy2)/g = (2*vox*voy)/g
Las "g" se cancelan. Pasamos los "0.5" dividiendo al miembro derecho. Se simplifican los "voy". Nos quedaría entonces:
voy = 4*vox
voy/vox = 4
Llegado a este punto, hay que recordar que:
voy = vo*Sin(θ)
vox = vo*Cos(θ)
Esto sale de la descomposición de la velocidad inicial en sus componentes rectangulares.
Reemplazando:
[vo*Sin(θ)]/[vo*Cos(θ)] = 4
Sin(θ)/Cos(θ) = 4
Tan(θ) = 4
Y despejando finalmente para "θ" obtenemos la respuesta:
θ = Tan-1(4) = 75.9638º
θ = 75.9638º
-
EJERCICIO ELECTROSTICA
Se muestra en la figura un ensamble de 3 condensadores ,cargados mediante una bateria de fuerza electromotriz "E" . Si la diferencia de potencial a traves del condensador C1 vale 4 voltios . ¿ cual es el valor de la fuerza electromotriz de la bateria?
c1 = 2 uf c2 = 6 uf C 3 = 8 uf
A mi sales como respuesta 8 voltios , estara bien
la opciones son :
a) 2 voltios b) 4 voltios c) 6 voltios D) 8 voltios E) 12 voltios
por favor ayúdame no se si estará bien , ayúdame con esta duda, por favor en que no estoy seguro si estar bien.
ESTA EN LA FIGURA
-


Antonio Silvio Palmitano
el 26/9/19Vamos con una orientación.
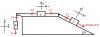
Tienes para el resorte de la izquierda:
L1i = 1,1 m (longitud inicial),
(L1i + ΔL1) (en m) (longitud final),
θ1 = 66° (ángulo de inclinación con respecto a la dirección vertical),
F1 = k1*ΔL1 (módulo de la fuerza elástica).
Tienes para el resorte de la derecha:
L2i = 0,4 m (longitud inicial),
(L2i + ΔL2) (en m) (longitud final),
θ2 = 37° (ángulo de inclinación con respecto a la dirección vertical),
F2 = k2*ΔL2 (módulo de la fuerza elástica).
Luego, estableces un sistema de referencia con origen de coordenadas en el punto de unión entre los dos resortes, con eje OX horizontal con sentido positivo hacia la derecha según tu figura, y con eje OY vertical con sentido hacia arriba; luego aplicas la Primera Ley de Newton (recuerda que los ángulos de inclinación de las fuerzas elásticas están medidos a partir de la dirección vertical, y observa que designamos con F al módulo de la fuerza externa aplicada), y tienes el sistema de ecuaciones:
-F1*sen(θ1) + F2*sen(θ2) = 0,
F1*cos(θ1) + F2*cos(θ2) - F = 0;
luego, sustituyes las expresiones de los módulos de las fuerzas elásticas (observa que remarcamos las incógnitas del sistema), y queda:
-k1*ΔL1*sen(θ1) + k2*ΔL2*sen(θ2) = 0 (1),
k1*ΔL1*cos(θ1) + k2*ΔL2*cos(θ2) - F = 0 (2).
Luego, observa que si superpones las dos figuras tienes dos triángulos rectángulos, de los que conoces sus ángulos interiores en el origen de coordenadas, las longitudes de los lados opuestos a dichos ángulos, y observa también que tienes planteadas las longitudes de sus hipotenusas, por lo que puedes plantear las relaciones trigonométricas (observa que aquí también remarcamos las incógnitas):
sen(θ1) = L1i/(L1i + ΔL1) (3),
sen(θ2) = L2i/(L1i + ΔL2) (4).
Luego, solo queda que reemplaces valores en las ecuaciones señaladas (3) (4) y resuelvas sus incógnitas, para luego reemplazar sus valores en las ecuaciones señaladas (1) (2), para luego resolver el sistema formado por ellas y obtener los valores de las constantes elásticas de los resortes (te dejo la tarea).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Buenas noches, me surgió una duda a la hora de resolver el siguiente ejercicio:
Conocemos la masa de un cuerpo que se suelta desde un punto y desciende sin rozamiento por una pista (con forma de 9 tumbado). Parte del reposo desde una altura h y la segunda circunferencia tiene un radio r. ¿Cómo se calcularía el módulo de la velocidad del cuerpo en un punto B (situado en un extremo del diámetro horizontal)?
¡Muchísimas gracias! :)


Antonio Silvio Palmitano
el 26/9/19Consideramos que el cuerpo desliza (es un bloque) y no rueda.
Considera que la energía potencial gravitatoria es igual a cero a nivel del punto más bajo de la circunferencia, y considera un eje de posiciones (alturas) OY vertical con sentido positivo hacia arriba.
Luego, planteas la expresión de la energía mecánica inicial (observa que tienes en tu enunciado: yi = h, vi = 0), y queda:
EMi = EPi + ECi = M*g*yi + (1/2)*M*vi2 = M*g*h + (1/2)*M*02 = M*g*h + 0 = M*g*h.
Luego, planteas la expresión de la energía mecánica en el punto B (observa que tienes en tu enunciado: yB = r, vB = a determinar), y queda:
EMB = EPB + ECB = M*g*yB + (1/2)*M*vB2 = M*g*r + (1/2)*M*vB2.
Luego, como tienes en tu enunciado que se desprecian las fuerzas de rozamiento, entonces puedes plantear conservación de la energía mecánica, y tienes la ecuación:
EMB = EMi, sustituyes expresiones, y queda:
M*g*r + (1/2)*M*vB2 = M*g*h, multiplicas por 2 y divides por M en todos los términos, y queda:
2*g*r + vB2 = 2*g*h, restas 2*g*r en ambos miembros, y queda:
vB2 = 2*g*h - 2*g*r, extraes factor común en el segundo miembro, y queda:
vB2 = 2*g*(h - r), extraes raíz cuadrada positiva en ambos miembros, y queda:
vB = √( 2*g*(h - r) ),
que es la expresión de la rapidez del bloque cuando alcanza un punto ubicado en un extremo del diámetro horizontal de la circunferencia, y observa que para que esta situación sea posible tienes que debe cumplirse la condición: h > r.
Espero haberte ayudado.
-
Hola, espero que puedas ayudar, de antemano gracias. Estoy viendo un tema de un libro (Mecanica vectorial para ingenieros-Estatica-Beer Johnson), que es momento de una fuerza, me he topado con un ejercicio que bajo mis procedimientos lo he resuelto, sin embargo me resultó un poco extenso; por otra parte buscando en el solucionario del libro, el ejercicio es resuelto de una forma más corta, ahora con la solución del libro hay una pequeña cosa que no comprendo, el ejercicio involucra un producto escalar, menciono que manejaba la idea que para que dos vectores puedan ser manejados por un producto escalar tienen que ser concurrentes, en el libro los vectores que están siendo multiplicados ( vector unitario AB y vector unitario P ) no tienen un punto en común para poder formar un ángulo, el libro realiza el producto y expresa un ángulo θ entre los 2 vectores, no visualizo de que forma se formaría el ángulo entre ellos, en grandes rasgos esa es mi pequeña duda. Anexo la solución que me proporciona el libro.
-
Se tiene dos condensadores C1 y C2 cargados a potencial diferentes V1 = 300 V y V2 = 100 V respectivamente .luego se unen en paralelo ,resultado que la diferencia de potencial entre placas de los condensadores es de 250 V. Determinar la relación C1 / C2 de las capacidades de los condensadores.
A mi sale 2,6
estarán bien por favor ayúdame con esta duda
cual seria de la opciones la respuesta correcta
a) 2,6 b) 5,0 c) 4,2 d) 3,8 e) 3,0
por favor ayúdame ya que el resultado que me sales no estoy seguro si están bien o no
por favor ayúdame con esta duda


Antonio Silvio Palmitano
el 26/9/19Planteas las expresiones de las cargas iniciales de los condensadores, y queda:
q1 = C1*V1 = C1*300 = 300*C1 (en C),
q2 = C2*V2 = C2*100 = 100*C2 (en C).
Luego, observa que cuando se conectan en paralelo, tienes que la carga total se redistribuye entre los dos condensadores, por lo que puedes plantear la ecuación (indicamos con mayúsculas a las cargas finales de los condensadores):
Q1 + Q2 = q1 + q2,
sustituyes las expresiones de las cargas iniciales de los condensadores en el segundo miembro, y queda:
Q1 + Q2 = 300*C1 + 100*C2 (1).
Luego, planteas la expresión de las cargas de los condensadores cuando están conectados en paralelo (recuerda que en este caso la diferencia de potencial es la misma para ambos dispositivos), y queda:
Q1 = C1*Vf = C1*250 = 250*C1 (2),
Q2 = C2*Vf = C2*250 = 250*C2 (3).
Luego, sustituyes las expresiones señaladas (2) (3) en el primer miembro de la ecuación señalada (1), y queda
250*C1 + 250*C2 = 300*C1 + 100*C2, restas 300*C1 y restas 250*C2 en ambos miembros, y queda:
-50*C1 = -150*C2, divides por -50 en ambos miembros, y queda:
C1 = 3*C2, divides por C2 en ambos miembros, y queda:
C1/C2 = 3,
por lo que tienes que la opción señalada (e) es la respuesta correcta.
Espero haberte ayudado.