-


Raúl RC
el 7/6/19Entiendo que te faltan datos, como la densidad del aluminio que es 2700 kg/m3
Calculamos el volumen del cubo:
Volumen = masa / densidad = 1000 / 2700 = 0.37037 m3
Ahora la longitud de cada arista (lado) del cubo V = a3 a = raíz cúbica de 0.37037 = 0.7181 m
El agua cubre la mitad del cubo, por lo tanto el volumen desalojado es la mitad: 0.37037 / 2 = 0.185185 m3
La fuerza de empuje la calculamos con el principio de Arquímedes E = Densidad del líquido · gravedad · volumen desalojado = 1000 · 9.81 · 0.185185= 1816.66 N
El peso aparente, (la fuerza normal ejercida por el cubo en el fondo) es igual a su peso (masa · gravedad) - Empuje = 1000 X 9.81 - 1816.66 = 7993.33 N
Para que la fuerza ejercida por el cubo en el fondo (su peso aparente) sea cero el mercurio debe de ejercer una fuerza de empuje de igual valor (7993.33) pero de sentido contrario. Despejamos el volumen de líquido que deberá de desalojar el cubo de aluminio: Volumen desalojado = Empuje / ( densidad del líquido · gravedad) = 7999.33 / (13600 · 9.81) = 0.05991m3
La base del cubo es un cuadrado de 0.7181 m de lado, calculemos la altura del prisma con esa base que ocupa un volumen de 0.05991 m3
V = Área de la base · altura, de donde altura = Volumen / área de la base = 0.05991 / 0.7181^2 = 0.1161 m, esa es la altura del cubo de aluminio que debe ser cubierta por el mercurio, es decir es el grosor de la capa de mercurio
Si el apartado b) fuera independiente del a) , entonces la fuerza de empuje producida por el mercurio tendría que ser igual al peso del cubo Peso = masa · gravedad = 1000 · 9.81 = 9810 N y el volumen desalojado sería 9810 / (13600 · 9.81) = 0.07352 m3 y la altura = 0.07352 /0.71812 = 0.1425 m -


Raúl RC
el 7/6/19Hola Shantal, antes de adjuntar un boletín con bastantes ejercicios sería interesante que antes "pasaras por clase" y vieras los vídeos relacionados con la temática que necesitas, recuerda que el esfuerzo ha de ser tuyo ;)
https://www.youtube.com/watch?v=QV0Iw0fdIWY
-


Raúl RC
el 7/6/19Hola Leon, lamento no poder ayudarte pero no resolvemos dudas universitarias que no tengan que ver específicamente con los vídeos ya grabados por el profe, como excepción hay algunos videos sobre el tema de caudal etc que puede te puedan ayudar, pero poco más, un saludo ;)
Hidraúlica - Caudal volumétrico -
Un coche de 1200 kg toma a 108 km/h una curva de 100 m de radio sin peraltar (es decir, su superficie es horizontal). Calcula la fuerza centrípeta necesaria para que no se salga de la carretera. por favor como resuelvo este ejercicio
-
Hola alguien me puede echar una mano? Gracias.
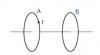
La figura representa dos bucles de corriente, A y B, que comparten el eje de simetría y son paralelos entre sí. Visto desde el lado izquierdo, el bucle A lleva una corriente que fluye en sentido contrario a las agujas del reloj. Determine la dirección de la corriente inducida en el bucle B y determine si los bucles se atraen o repelen entre sí, en los siguientes casos:
(a) La magnitud de I aumenta con el tiempo.
(b) I es constante, pero la distancia entre A y B aumenta con el tiempo.


Antonio Silvio Palmitano
el 6/6/19Observa que la corriente que circula por la espira A cuya intensidad es IA produce un campo magnético que atraviesa la espira B, y cuyo sentido para los puntos interiores a la espira B es de derecha a izquierda según tu figura.
a)
Observa que la cantidad de líneas de campo producido por la espira A que atraviesan la espira B están en aumento, por lo que la corriente inducida debe oponerse a esta variación, según la Ley de Lenz.
Por lo tanto, tienes que la corriente inducida, cuya intensidad designamos IB, debe tener sentido favorable a las agujas del reloj, si se la observa desde el lado izquierdo,
y como las intensidades de corriente en ambas espiras son paralelas con sentidos opuestos, tienes que las dos espiras se repelen entre sí.
b)
Observa que la cantidad de líneas de campo producido por la espira A que atraviesan la espira B están en disminución, a medida que las espiras se separan cada vez más, por lo que la corriente inducida debe oponerse a esta variación, según la Ley de Lenz.
Por lo tanto, tienes que la corriente inducida, cuya intensidad designamos IB, debe tener sentido contrario a las agujas del reloj, si se la observa desde el lado izquierdo,
y como las intensidades de corriente en ambas espiras son paralelas con sentidos iguales, tienes que las dos espiras se atraen entre sí.
Espero haberte ayudado.
-
Por favor, cómo resolver este ejercicio?
-
Un vagón de 1100 kg de masa que se ha soltado de un tren se dirige a 5m/s hacia un gatito que duerme plácidamente en la vía. En un instante aparece Supermán e intenta pararlo tirando del vagón hacia atrás con una cadena que tiene una resistencia de 450 N. No hay rozamiento.
-
a) Utilizando la 2a Ley de Newton, calcula la aceleración máxima con la que Supermán puede frenar el vagón.
-
b) ¿Cuánto tiempo estará tirando Superman de la cadena hasta que pare el vagón?
-
c) ¿A qué distancia como mínimo debía estar el gatito del vagón cuando Superman
empezó a frenarlo si no lo atropelló?
Muchas gracias.
-


Antonio Silvio Palmitano
el 6/6/19Considera un sistema de referencia con eje de posiciones OX paralelo a la vía, con instante inicial (ti = 0) correspondiente al momento en que el superhombre toma contacto con el vagón, con origen de coordenadas en el punto correspondiente, y con sentido positivo acorde al desplazamiento del vagón, y observa que las fuerzas verticales (peso y acción normal de los rieles) no afectan al desplazamiento horizontal del vagón.
Luego, observa que la única fuerza con dirección horizontal que está aplicada sobre el vagón es la que ejerce el superhombre, de la que indicamos su módulo y sentido:
F = 450 N, opuesto al desplazamiento del vagón.
Luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
-F = M*a, reemplazas el valor del módulo de la fuerza aplicada y de la masa del vagón, y queda:
-450 = 1100*a, y de aquí despejas:
a = -9/22 m/s2 ≅ -0,409 m/s2.
Luego, planteas la expresión de la función velocidad de Movimiento Rectilíneo Uniformemente Variado, y queda:
v = vi + a*t,
aquí reemplazas valores, y queda:
v = 5 - (9/22)*t;
luego, planteas la condición de detención del vagón, y queda:
v = 0, sustituyes la expresión de la función velocidad, y queda:
5 - (9/22)*t = 0, y de aquí despejas:
t = 110/9 s ≅ 12,222 s.
Luego, planteas la expresión de la función posición de Movimiento Rectilíneo Uniformemente Variado, y queda:
x = xi + vi*t + (1/2)*a*t2,
aquí reemplazas valores, y queda:
x = 0 + 5*(110/9) + (1/2)*(-9/22)*(110/9)2,
aquí cancelas el término nulo, resuelves términos, y queda:
x = 550/9 - 275/9,
resuelves, y el valor de la distancia de detención del vagón queda:
x = 275/9 m ≅ 30,556 m.
Espero haberte ayudado.
-
-


Antonio Silvio Palmitano
el 6/6/19Suponemos que el tronco se hunde con su eje de simetría en la dirección vertical.
Tienes el valor de la densidad de masa del agua:
δa = 1000 Kg/m3.
Luego, como tienes el valor de la densidad relativa de la madera con respecto al agua, tienes que la densidad de la madera queda expresada:
δm = δrel*δa = 0,425*1000 = 425 Kg/m3.
Luego, planteas la expresión del módulo del peso del tronco cilíndrico, y queda:
P = δm*Vt*g = δm*π*(d2/4)*ht*g.
Luego, planteas la expresión del módulo del empuje (observa que indicamos con hs a la altura del volumen cilíndrico sumergido), y queda:
E= δa*Vs*g = δa*π*(d2/4)*hs*g.
Luego, aplicas la Primera Ley de Newton (observa que consideramos un sistema de referencia con eje OY vertical con sentido positivo hacia arriba), y queda la ecuación:
E - P = 0, sustituyes las expresiones de los módulos de las fuerzas, y queda:
δa*π*(d2/4)*hs*g = δm*π*(d2/4)*ht*g,
divides en ambos miembros por π*(d2/4)*g, simplificas, y queda:
δa*hs = δm*ht,
divides por x en ambos miembros, y queda:
hs = δm*ht/δa,
reemplazas valores, y queda:
hs = 425*4,50/1000,
resuelves, y queda:
hs = 1,9125 m.
Espero haberte ayudado.