-
Antonio Silvio Palmitano
el 3/3/18Vamos con una orientación.
Llamamos I a la matriz identidad de orden dos; luego, como I*X = X, sustituyes en el segundo término del primer miembro de la ecuación, y queda:
A*X - 2*I*X = B;
luego, extraes factor común por la derecha en el primer miembro, y queda:
(A - 2*I)*X = B;
luego, si la matriz (A - 2*I) es invertible, multiplicas por la izquierda por su matriz inversa en ambos miembros, y queda:
(A - 2*I)-1*(A - 2*I)*X = (A - 2*I)-1*B;
luego, resuelves el producto de matrices inversas entre sí que tienes en los dos primeros factores, y queda:
I*X = (A - 2*I)-1*B;
luego, aplicas la propiedad del elemento neutro de la multiplicación de matrices en el primer miembro, y queda:
X = (A - 2*I)-1*B.
Luego, tienes en tu enunciado la expresión de la matriz A, y luego, observa que la expresión de la matriz (A - 2*I) es:
A - 2*I =
-1 -1
1 0,
que es una matriz cuadrada de orden dos, cuyo determinante es igual a 1, que es distinto de cero, por lo que es una matriz invertible.
Espero haberte ayudado.
-
Hola, podrías hacer un vídeo de sistemas de ecuaciones lineales para 4ºESO. Gracias
Ángel
el 4/3/18Son del nivel que te puedes encontrar en la ESO:
-
Fernando gasta en la entrada de cine las 2/5 partes de su paga semanal,. Después, gasta una tercera parte de lo que le queda en palomitas y con una sexta parte de lo que le queda compra una rifa escolar. Al final le quedan 5€ ¿Cuál es su paga semanal?
Antonio Silvio Palmitano
el 3/3/18Tal como dice el colega Julián, puedes designar a la paga semanal con x.
Luego, tienes los gastos:
(2/5)x: gasto en comprar la entrada de cine (observa que queda: x - (2/5)x = (3/5)x en poder de Fernando);
(1/3)((3/5)x = (3/15)x = (1/5)x: gasto en comprar palomitas (observa que queda: (3/5)x - (1/5)x == (2/5)x en en poder de Fernando);
(1/6)(2/5)x = (2/30)x = (1/15)x: gasto en comprar la rifa escolar (observa que queda. (2/5)x - (1/15)x = (5/15)x = (1/3)x en poder de Fernando);
luego, tienes que el sobrante es 5 euros, por lo que puedes plantear la ecuación:
(1/3)x = 5, multiplicas por 3 en ambos miembros, y queda: x = 15 euros;
luego, tienes los gastos:
(2/5)*15 = 30/5 = 6 euros: gasto en la entrada de cine;
(1/5)*15 = 15/5 = 3 euros: gasto en comprar palomitas;
(1/15)*15 = 15/15 = 1 euro: gato en comprar la rifa escolar;
y observa que la suma total de los gastos es 10 euros, por lo que el sobrante son 5 euros.
Espero haberte ayudado.
-
Si estas jugando y la carta de tu mazo es 1/2, ¿que cartas te conviene que tengan los otros jugadores? ¿y si sacas 1/4?
Ángel
el 3/3/18 -
Ángel
el 3/3/18https://www.vitutor.com/pro/2/a_4.html
https://www.vitutor.com/pro/2/a_5.html
https://www.vitutor.com/pro/2/a_11.html
Datos
P(detergente)=0.77
P(blanqueador)=0.85
P(detergente ∩ blanqueador)=0.65
Queremos saber a quienes se les obsequia con un cepillo, será todos menos los que compren las dos cosas, esto es P(cepillo)= P(detergente ∪ blanqueador) -P(detergente ∩ blanqueador)
Nos falta saber P(detergente ∪ blanqueador) y conocemos la fórmula:P(A ∪ B)= P(A) + P(B) - P(A ∩ B)
Que extrapolada a nuestro ejercicio es:
P(detergente ∪ blanqueador)= P(detergente) + P(blanqueador) - P(detergente ∩ blanqueador)
P(detergente ∪ blanqueador)= 0.77+0.85-0.65 = 0.97
Entonces P(cepillo)= 0.97-0.65= 0.32
Y si asisten 450 personas concluimos que se entregarán 450*0.32= 144 cepillos (respuesta B)
Rasyer
el 3/3/18Para calcular las personas que únicamente han comprado un producto tenemes que valorar estos dos grupos:
Grupo 1 --> Las que no han comprado el primer producto pero si el segundo.
Grupo 2 --> Las que sí han comprado el primer producto pero no el segundo.
Ahora escribimos los porcentages para aclararnos:
SI Comprado NO comprado Primer producto 77% 23% Segundo producto 85% 15% Calculamos cuanta gente hay en cada grupo:
Grupo 1: 450 * 0.23 * 0.85 = 450 * 0.20 = 90
Grupo 2: 450 * 0.77 * 0.15 = 450 * 0.12 = 54
Total de personas que han comprado únicamente un producto: 90+54 = 144
Antonio Silvio Palmitano
el 3/3/18En tu enunciado tienes las probabilidades:
P(D) = 0,77, P(B) = 0,85 y p(D∩B) = 0,65.
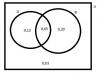
Observa el diagrama, y tienes las probabilidades:
P(D-B) = 0,12, p(B-D) = 0,20 y p( ∼(D∪B) ) = 0,03.
Luego, puedes plantear el suceso:
A: "un asistente en particular compra uno solo de los productos",
y observa que su probabilidad es:
p(A) = p( (D-B) ∪ (B-D) ) = 0,12 + 0,20 = 0,32.
Luego, tienes que la cantidad esperada de asistentes que compre un solo producto (sobre un total: n = 450) es:
E(A) = n*p(A) = 450*0,32 = 144.
Espero haberte ayudado.
-
Hola , buenos días.
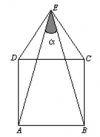
Alguien me podría ayudar con el siguiente problema de optimización: " Determina los puntos de la curva y= x2 que estén a una distancia mínima del punto (4,0) . Muchas gracias.
Ángel
el 4/3/18O bien lo haces con algún programa matemático (symbolab o wolfram) por ejemplo.
O bien empleas el método de bisección (reduciendo el intervalo en el que se encuentra x a la mitad en cada paso) para obtener un valor aproximado de la raíz del denominador de la derivada al que te refieres:
Teniendo la subfunción g(x)= 2x3+x-4, si queremos saber cuando g(x)=0 :
*Tened en cuenta que el cero estará entre los valores en los que haya un cambio de signo.
g(0)= -4
g(1)= -1
g(2)= 14
(entonces habrá una raíz entre x=1 y x=2)
...seguimos acotando ese valor
g(1.5)=4.25
g(1.25)=1.15625
(entonces habrá una raíz entre x=1 y x=1.25 porque g(1)<0 y g(1.25)>0
g(1.125)= -0.02734375 (casi cero!)
Ya creo que hemos llegado a una aproximación bastante buena, por lo que concluiríamos que la raíz es aproximadamente 1.125
-
Buenas noches,
Como puedo encontrar un campo conservativo F, tal que ∫F ds=0 sin que C sea una trayectoria cerrada
Antonio Silvio Palmitano
el 3/3/18Por ejemplo, puedes considerar un campo constante:
F = < 0,0,-10>,
y una trayectoria recta perpendicular al campo en todos sus puntos, por ejemplo con la función vectorial de posición:
r(t) = <t,t,0>, con 1 ≤ t ≤ 3;
cuya derivada primera queda.
r ' (t) = <1,1,0>.
Luego, plantea la integral de línea del campo vectorial, y queda:
∫C F•ds = 1∫3 F( r(r) )•r ' (t)*dt = 1∫3 <0,0,-10>•<1,1,0>*dt = resuelves el producto escalar = 1∫3 0*dt = 0.
Espero haberte ayudado.