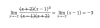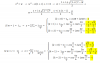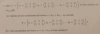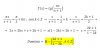-
Buenas tardes, tengo una duda. Si estamos calculando un límite y es necesario factorizar el numerador o el denominador, si al resolver la ecuación salen todas las soluciones iguales. ¿Cuando se factoriza se pondría una solo o todas?
-


Antonio Silvio Palmitano
el 29/1/20Vamos con una orientación.
Has planteado correctamente la ecuación característica:
(6 - d)*(4 - d)*(2 - d) - [4*(4 - d)*(-1)] = 0,
resuelves el coeficiente en el segundo término, y queda:
(6 - d)*(4 - d)*(2 - d) + 4*(4 - d) = 0,
extraes factor común en el primer miembro, y queda:
(4 - d)*[(6 - d)*(2 - d) + 4] = 0,
y por anulación de un producto, tienes dos opciones:
1°)
4 - d = 0, y de aquí despejas: d = 4;
2°)
(6 - d)*(2 - d) + 4 = 0, distribuyes el primer término, y queda:
12 - 6d - 2d + d2 + 4 = 0, reduces términos semejantes, ordenas términos, y queda:
d2 - 8d + 16 = 0, factorizas el primer miembro (observa que es un trinomio cuadrado perfecto), y queda:
(d - 4)2 = 0, y de aquí despejas: d = 4.
Luego, puedes continuar la tarea.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 29/1/20En tu imagen es erróneo el coeficiente 48, observa que queda: (6 - d)*(4 - d) = 24 - 6d - 4d + d2= 24 - 10d + d2;
pero de todas maneras, considera resolver el ejercicio como te lo hemos propuesto, porque con la expresión del polinomio característico factorizada, es mucho más sencillo obtener los autovalores (o valores propios).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 29/1/20Tienes una ecuación polinómica con coeficientes complejos, por lo que tienes que tiene seis soluciones, de acuerdo con el Teorema Fundamental:
z6 + i*z3 = 0,
extraes factor común en el primer miembro, y queda:
z3*(z3 + i) = 0.
Luego, por anulación de una multiplicación, tienes dos opciones:
1°)
z3 = 0, extraes raíz cúbica en ambos miembros, y queda:
z = 0, que es una raíz cuya multiplicidad es tres;
2°)
Z3 + i = 0, restas i en ambos miembros, y queda:
Z3 = -i, expresas al segundo miembro en forma exponencial, y queda:
Z3 = ei*(3π/2+2*k*π), con k ∈ Z, extraes raíz cúbica en ambos miembros, y queda:
Z = ei*(3π/2+2*k*π)/3, con k = 0, 1, 2;
luego, evalúas para los valores del parámetro, y queda:
Z0 = ei*(3π/2+2*0*π)/3,
Z1 = ei*(3π/2+2*1*π)/3,
Z2 = ei*(3π/2+2*2*π)/3,
resuelves las expresiones de los argumentos en los exponentes, y queda:
Z0 = ei*π/2,
Z1 = ei*7π/6,
Z2 = ei*11π/6,
que son las tres raíces cuya multiplicidad es 1.
Espero haberte ayudado.
-


Jose Ramos
el 29/1/20Este ejercicio tiene un error en el enunciado, le sobra ese 4/7 (Yo al menos no entiendo que quiere decir con "4 plumas 4/7 "..
El enunciado normal sería: "Un niño que tenía una caja de plumas, gasta los 2/7 más 4 plumas; entonces le quedan los 2/3 de las que tenía. ¿Cuántas plumas había en la caja?"
Así sería: x - (2/7 x + 4) = 2/3 x. Siendo x el número de plumas que había en la caja. Resolviendo queda: x - 2/7 x - 4 = 2/3 x ; x- 2/7 x - 2/3 x = 4 ; (21x - 6x -14x)/21 = 4 ; x = 84


salvador nicolas
el 29/1/20Hola, gracias, por responder tan pronto, a mi tambien me descoloca un poco esa fraccion , este problema es de un libro de Aritmetica razonada,de
los años 40, de editorial Bruño, pero la solucion que da es la siguiente: si 1 ⁄ 3, es el total de lo que gasta, entonces 2/ 7 + 4 + 4 / 7 = 1/3----
de donde 1/ 3 − 2/ 7 = 4+4/7⇔ desarrollando tenemos 1/ 21 = 32/7⇔ de donde 1 = 21 x 32 / 7 = 96 , que es la solucion he intentado llegar al mismo resultado con otro tipo de planteamiento, porque el problema este del libro no lo entiendo,, si me podeis ayudar con un razonamiento diferente
logico
______
-
Hola, alguien me puede ayudar con esto?:
Hallar las ecuaciones matriciales de un giro de ángulo (α) en el espacio mediante el cual un punto P(x,y) se transforma en otro punto P’(x’,y’)
Gracias :)
-
Buenas, me han dicho que me falta una solución que es z3=-i, todas las demás las he hallado. Me pedían resolver la ecuación de la foto, lo he hecho mediante ruffini, si alguien me puede ayudar a saber que esta mal se lo agradecería.


Antonio Silvio Palmitano
el 29/1/20Observa que tienes una ecuación polinómica con coeficientes complejos cuyo grado es seis, por lo que tienes que sus soluciones son seis, de acuerdo con el Teorema Fundamental, que seguramente has visto en clase.
Has planteado correctamente la sustitución (cambio de incógnita): z3 = w (1), y has obtenido las dos soluciones primarias: w = 1 y w = i, a la que estudias por separado, y tienes:
1°)
Para w = 1, sustituyes en la ecuación señalada (1), y queda:
z3 = 1, expresas al segundo miembro en forma exponencial, y queda:
z3 = ei*2*k*π, con k ∈ Z, con k = 0, 1 o 2;
luego, elevas a la 1/3 en ambos miembros de esta ecuación, y queda:
zk = ei*2*k*π/3, reemplazas los valores el parámetro, y queda:
z0 = ei*2*0*π/3 = e0 = 1,
z1 = ei*2*1*π/3 = ei*2π/3,
z2 = ei*2*2*π/3= ei*4π/3.
2°)
Para w = i, sustituyes en la ecuación señalada (1), y queda:
Z3 = i, expresas al segundo miembro en forma exponencial, y queda:
Z3 = ei*(4*m+1)*π/2, con m ∈ Z, con m = 0, 1 o 2;
luego, elevas a la 1/3 en ambos miembros de esta ecuación, y queda:
Zm = ei*(4*m+1)*π/6, reemplazas los valores el parámetro, y queda:
Z0 = ei*(4*0+1)*π/6 = ei*π/6,
Z1 = ei*(4*1+1)*π/6 = ei*5π/6,
Z2 = ei*(4*2+1)*π/6 = ei*9π/6 = ei*3π/2 = -i.
Espero haberte ayudado.
-
Alguien me puede decir como hacer este cambio de base? No entiendo muy bien como llegar a hacer los cálculos, normalmente tengo matrices más "normales" un calculo con inversa y listo...
a) Cuales son las coordenadas del vector v... en la base: B
b) Y las coordenadas del vector w... en la canónica?
-


David
el 29/1/20π x / (x+1) debe ser distinto de 0+180k.... porque la tangente de 0º, 180º, 360º, etc.. no existe...
Por tanto π x / (x+1) ≠ 180k... Y resuelves la ecuacion...
Representación de la función tangente
Tienes un video de la funcion tangente