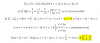Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Hanan
el 5/4/17

Que es la factorizacion de polinomios?
Gracias.

••0 voto/s
•
César
el 5/4/17
Descomposición factorial
•0 voto/s
•

Cancelar
Guillem De La Calle Vicente
el 5/4/17

x es el valor de un field goal y y es el valor de un tiro libre. La mayor puntuación imposible de alcanzar es 119. ¿Qué es 3x + 2y?
x e y son enteros positivos, x <y, x + y deben ser minimizados.

••0 voto/s
•
César
el 5/4/17
Vale Guille, queda anotado.

•0 voto/s
•
Guillem De La Calle Vicente
el 5/4/17
Tengo la solución:
Des de que 119 = (3·1)+(58·2), todas las soluciones en pares enteros (x, y) de 3x+2y=119 son x=1+2t, y=58-3t (t ∈ ℤ).
Para 0<x<y, tenemos 0≤t≤11. Como que x+y=59-t se tiene que minimizar, escogemos t=11. Eso nos da el valor mínimo 48, y corresponde con x=23 e y=25.

•0 voto/s
•

Cancelar
anonimo
el 5/4/17

¿cual es el organo equivalente a la comisaria europea de salud, a escala nacional?
Es una pregunta en un tema de la EU

••0 voto/s
•
David
el 17/4/17
Lo siento pero tu duda no es propia de este foro...

•0 voto/s
•

Cancelar
Rafael Pita Olivera
el 5/4/17

Chicos me ayudáis con esto porfa? El apartado a) lo he hecho con determinantes y el rango y si que me ha salido pero el apartado b) no me sale de ninguna forma... me ayudáis? Os pongo el ejercicio y su solución

••0 voto/s
•
César
el 5/4/17
Correcto Rafael

•1 voto/s
•
Guillem De La Calle Vicente
el 5/4/17

•1 voto/s
•
Rafael Pita Olivera
el 5/4/17
Si no es mucho pedir... ¿me podrías explicar porque se sabe que la y=y, z=z ? ¿Y porque se sabe que los parámetros son z e y, porque no podría ser la x?

•0 voto/s
•
Guillem De La Calle Vicente
el 6/4/17
Puedes poner lo que quieras, pero normalmente se empieza por el final. Si es un parámetro, z=z, y así.

•1 voto/s
•

Cancelar
sus
el 5/4/17

De todos los triangulos isosceles inscritos en una circunferencia de 5 cm de radio, halla las dimensiones del que tiene mayor área.

Entiendo la optimización pero al ser una circunferencia estoy muy confusa y liada. me ayudáis. Solo a plantear el resto es coser y cantar! GRACIAS

••0 voto/s
•
César
el 5/4/17

•1 voto/s
•
César
el 5/4/17
Revisalo Sus

•0 voto/s
•
sus
el 5/4/17
César no se de donde salió el 15 que tienes en la función derivada! he deducido que cambiaste la R por 5 que es el valor del radio pero yo cuando derivo llego a 2h(10-2h) no 15.

•0 voto/s
•
sus
el 5/4/17
Nada ya he llegado a ello. Estaba comiendome la primera parte de la derivada. Muchas gracias por tu ayuda! Un saludo!

•0 voto/s
•

Cancelar
Hanan
el 5/4/17

Hola
Utiliza el teorema del resto para calcular el resto de estas divisiones.
Como se calcula??
(x⁶_ 3x⁵+ x³_ 2x²_ 6x _ 3):(x+2)
Gracias.

••0 voto/s
•
César
el 5/4/17
Teorema del resto
•0 voto/s
•

Cancelar
Carla Extremera Torras
el 5/4/17

Como se haría el c paso a paso?

••0 voto/s
•
Antonius Benedictus
el 5/4/17

•0 voto/s
•
César
el 5/4/17

•0 voto/s
•
Carla Extremera Torras
el 5/4/17
ose acuando dice punto de intersección hace referencia al punto medio, a M?

•0 voto/s
•

Cancelar
Ivan Celda Soler
el 5/4/17

encuentra 2 puntos de cada una de las rectas siguientes y utilízalos para dar un vector director en cada caso:
a) y= 2x-3 b)y=3 c)x-2y+1=0

••0 voto/s
•
César
el 5/4/17

•0 voto/s
•
Ivan Celda Soler
el 5/4/17
Podría explicármelo por favor?

•0 voto/s
•

Cancelar
Rafa Jiménez
el 5/4/17

Hola, me podéis ayudar con este ejercicio:
La producción mensual de una empresa, en miles de unidades, viene dada por Q(x,y)= 40x/(5+x) + 40/(10+y) siendo x, y los gastos de mano de obra y de materia prima en miles de euros. Los gastos fijos de la empresa son de 10000 euros/mes y el presupuesto de gastos totales está limitado a 25000 euros/mes. Hallar como se deben de distribuir los gastos para obtener una producción máxima.
Gracias

••0 voto/s
•
Guillem De La Calle Vicente
el 5/4/17
¿Podrías mostrar que has hecho hasta ahora?

•0 voto/s
•

Cancelar
Nico
el 5/4/17

hola buenass, necesitaria una mano con este limite, no tengo claro este tipo de limites, a mi entender daria 0 pero parece que da 1/3

••0 voto/s
•
Antonius Benedictus
el 5/4/17

•0 voto/s
•
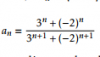
Nico
el 6/4/17
hola Antonio, tengo una duda, en estos casos (potencias) donde el exponente del numerador es menor que el denominador , los limites se resuelve diferente , no? Porque cuando tenemos un limite de cociente de polinomios, donde el grado del denominador es mayor que el numerador el limite es cero.., esto no se cumple para las potencias verdad?

•0 voto/s
•

Cancelar