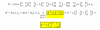Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

jose tomas perez martinez
el 2/4/17

Hola, ¿como se pasa de ecuación general en contiuna, parametrica o vectorial? en tercera dimension 2 bachillerato cientifico

••0 voto/s
•
Antonius Benedictus
el 2/4/17

•1 voto/s
•

Cancelar
Meiko Benegas
el 2/4/17

Buenas! Alguien me puede explicar brevemente cómo se haría una composición de dos funciones definidas a trozos?

••0 voto/s
•
Antonius Benedictus
el 2/4/17
Sube un ejercicio y lo intentamos.

•1 voto/s
•
Meiko Benegas
el 4/4/17
f(x) = {x^2 - x x<= -1 ; -x x> -1}
g(x)= {3 - x x <= 1 ; (x+1)^2 x> 1}

Calcular : (fog)(-1), (fog)(0), (gof)(0), (gof)(4).

•0 voto/s
•

Cancelar
Pedro
el 2/4/17

••0 voto/s
•
Antonius Benedictus
el 2/4/17
Función exponencial
•0 voto/s
•
Pedro
el 2/4/17
Muchas gracias, Antonio. Pero esta función es un poco más complicada que en el vídeo.

•0 voto/s
•

Cancelar

Cristina
el 2/4/17

Como se resuelve 2x-[3-4x-(1-2x)]-(7-4x)=1

Gracias

••0 voto/s•

Vanessa
el 2/4/17

Espero no haber fallado.

simplificando
2x + -1 [3 + -4x + -1 (1 + -2x)] + -1 (7 + -4x) = 1
2x + -1 [3 + -4x + (1 * -1 + -2x * -1)] + -1 (7 + -4x) = 1
2x + -1 [3 + -4x + (-1 + 2x)] + -1 (7 + -4x) = 1

Reordenar los términos:
2x + -1 [3 + -1 + -4x + 2x] + -1 (7 + -4x) = 1

Combina los términos semejantes: 3 + -1 = 2
2x + -1 [2 + -4x + 2x] + -1 (7 + -4x) = 1

Combina los términos semejantes: 4x + 2x = -2x
2x + -1 [2 + -2x] + -1 (7 + -4x) = 1
2x + [2 * -1 + -2x * -1] + -1 (7 + -4x) = 1
2x + [-2 + 2x] + -1 (7 + -4x) = 1
2x + -2 + 2x + (7 * -1 + -4x * -1) = 1
2x + -2 + 2x + (-7 + 4x) = 1

Reordenar los términos:
-2 -7 + + 2x + 2x + 4x = 1

Combina los términos semejantes: -2 + -7 = -9
-9 + 2x + 2x + 4x = 1

Combina los términos semejantes: 2x + 2x = 4x
-9 + 4x + 4x = 1

Combina los términos semejantes: 4x + 4x = 8x
-9 + 8x = 1

Resolviendo
-9 + 8x = 1

Resolver para la variable 'x'.

Mover todos los términos que contienen X a la izquierda, todos los demás términos a la derecha.

Añadir '9' a cada lado de la ecuación.
-9 + 9 + 8x = 1 + 9

Combina los términos semejantes: -9 + 9 = 0
0 + 8x = 1 + 9
8x = 1 + 9

Combina los términos semejantes: 1 + 9 = 10
8x = 10

Divide cada lado '8'.
x = 1,25 (x=10/8, si no pide decimales podemos simplificar a: x=5/4)

•1 voto/s•

Guille
el 2/4/17

2x-(3-4x-1+2x)-7+4x=1

2x-3+4x+1-2x-7+4x=1

8x-9=1

8x=10

X=10/8

•1 voto/s•

Nina
el 2/4/17

(2010-septiembre-2) 4. Considere la matriz.

a) Compruebe que cumple la igualdad A2 - 5A = I2, donde I2 es la matriz identidad
de orden 2.
b) Utilice esta igualdad para calcular la matriz inversa de A.

En el apartado A me ha dado que A2-5A da I pero el apartado b me da una respuesta que no coincide con la del solucionario , alguien me podria ayudar por favor?

••0 voto/s
•
Antonius Benedictus
el 2/4/17

•0 voto/s
•
Nina
el 2/4/17
Antonio , tengo otra duda, por que al sacar factor común de A queda 5I ?
Muchas gracias por la ayuda!!

•0 voto/s
•
Antonius Benedictus
el 2/4/17
Porque ha de quedar una matriz, no un número.
En álgebra numérica:
35x-7=7(5x-1)
Al sacar 7 factor queda 1.
En matrices, la matriz que juega el papel de 1 es I (identidad)

•0 voto/s
•
Antonius Benedictus
el 2/4/17
En números:
35x-7=7(5x-1)
Al sacar factor común queda 1 (el elemento neutro de la multiplicación).
A^2 -A= A(A-I)
Queda I la matriz que hace el papel de 1 en la multiplicación de matrices.
Finalmente:
A^2 -5A=A(A-5I)
No puede que dar un número suelto, sino una matriz.

•0 voto/s
•
Nina
el 2/4/17
Muchísimas gracias por su ayuda Antonio !!

•0 voto/s
•

Cancelar
Alfonso Sampedro
el 2/4/17

Como se obtendría la asintota oblicua de esta función? Gracias de antemano :)
f(x)= (e^x-1)/2

••0 voto/s
•
Antonius Benedictus
el 2/4/17

•1 voto/s
•

Cancelar
Javier Torrecilla
el 2/4/17

Por qué se obtienen dos rectas a partir de ecuación punto-recta?

••0 voto/s
•
Ángel
el 3/4/17
Tienes que preguntar a Guillem que fue el quehizo este trabajo.

•0 voto/s
•

Cancelar
lalis
el 2/4/17

periemtro y area de circulos

••0 voto/s
•
Ángel
el 3/4/17

•0 voto/s
•

Cancelar
Carmen Rosa Cabrera Castillo
el 2/4/17

2x-8 -22-x =2
____ _____
10 3
Por favor me podrían explicar el valor de la x en este caso

••0 voto/s
•
Antonius Benedictus
el 2/4/17

•0 voto/s
•

Cancelar
Sergio Jiménez
el 2/4/17

Para comprobar el resultado:
Considerando que cos15=0,9659 , aproxima sin usar calculadora.
a)sen75

••0 voto/s
•
Antonius Benedictus
el 2/4/17
Por ser ángulos complementarios, sin 75º=cos 15º

•1 voto/s
•

Cancelar