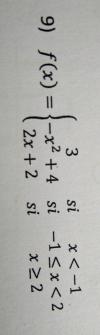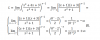logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Gabriela
    el 18/3/17

    Hola necesito dar una base del subespacio de matrices de traza 0 de M(nxn)

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/3/17

    Si d_1, d_2, ..., d_n son los elementos de la diagonal principal, entonces: d_1+d_2+...+d_n=0  (una ecuación implícita).

    Entonces, la dimensión es n^2 -1.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Matemáticas
    el 18/3/17

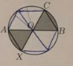
    Si tenemos un círculo con centro O y diametros AB y CX, de forma que los segmentos OB y BC son iguales. Qué parte de la área del círculo está ombreada?

       (A) 3/8

       (B) 2/7

       (C) 1/3

       (D) 2/5

       (E) 4/11



    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 18/3/17

    Parece que 2/6=1/3, no? :D

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonio Silvio Palmitano
    el 18/3/17

    Observa que los triángulos OBC y OAX son equiláteros, y que la medida de sus ángulos interiores con vértice O es α = 60° = π/3 rad.

    Luego, observa que las dos porciones sombreadas son sectores circulares congruentes, por lo que el área de la región sombreada (As) es igual al doble del área de uno de dichos sectores circulares (Asc para cada uno), y observa que cada sector circular (cuya área señalamos como Ac) corresponde a una sexta parte del círculo completo, por lo tanto tenemos:

    As = 2*Asc = 2*(1/6)Ac = (1/3)*Ac,

    por lo que concluimos que el área sombreada es igual a la tercera parte del área del círculo, por lo que tenemos que la opción C es la respuesta correcta.

    Espero haberte ayudado.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Jose Manuel
    el 18/3/17

    Alguien me ayuda con el siguiente ejercicio?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/3/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Pablo Reyes
    el 18/3/17
    flagflag


    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 17/4/17

    Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

    Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
  • icon

    andres
    el 18/3/17

    Buenas necesito ayuda para calcular la función a trozos de: |3x-2| lo que no entiendo son los signos por ejemplo cuando utilizamos el signo + para operar  es igual a x≥2/3 lo que no entiendo es el porqué de ≥. Muchas gracias!

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 18/3/17

    Recuerda la definición de función valor absoluto:

    |u| = 

     u              si u ≥ 0

    -u              si u < 0.

    Luego, tienes la función cuya expresión es:

    f(x) = |3x - 2|,

    aplicas la definición (observa que en esta expresión tienes: u = 3x - 2) y queda:

    f(x) =

     3x - 2                       si 3x - 2 ≥ 0 (haces pasaje de término y queda: 3x ≥  -2, haces pasaje de factor como divisor y queda: x ≥ 2/3)

    -(3x - 2)                    si 3x - 2 < 0 (haces pasaje de término y queda: 3x <  -2, haces pasaje de factor como divisor y queda: x < 2/3)

    distribuyes el signo en la expresión de la segunda rama, y la expresión de la función queda:

    f(x) = 

     3x - 2                     si x ≥ 2/3

    -3x + 2                    si x < 2/3

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    leire
    el 18/3/17

    Buenas! Necesito ayuda con esta ecuación trigonométrica. Por más que le doy vueltas no me sale... Gracias!


    reply•thumb_up•0 voto/s•flag
    icon

    César
    el 18/3/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonio Silvio Palmitano
    el 18/3/17

    Recuerda la identidad trigonométrica del seno del doble de un ángulo: sen(2x) = 2*senx*cosx, 

    luego sustituyes y la ecuación queda:

    2*senx*cosx*cosx = 6*sen3x,

    reduces factores en el primer miembro y queda:

    2*senx*cos2x = 6*sen3x,

    divides por 2 en ambos miembros y queda:

    senx*cos2x = 3*sen3x,

    haces pasaje de término y queda:

    senx*cos2x - 3*sen3x = 0,

    extraes factor común y queda:

    senx*(cos2x - 3*sen2x) = 0,

    luego, por anulación de un producto tienes dos opciones:

    1)

    senx = 0, compones con la función inversa del seno en ambos miembros y queda:

    x = 0, ±π, ±2π, ±3π, .... que en general pueden expresarse:

    x = k*π, con k ∈ Z;

    2)

    cos2x - 3*sen2x = 0, haces pasaje de término y queda:

    - 3*sen2x = - cos2x, haces pasajes de factores como divisores y queda:

    sen2x/cos2x = 1/3, aplicas la identidad trigonométrica para la tangente en función de seno y coseno y queda:

    tan2x = 1/3, luego haces pasaje de potencia como raíz y tienes dos opciones:

    a)

    tanx = √(1/3), que corresponde a ángulos del primero y del tercer cuadrante, cuyas expresiones generales son:

    x = π/6 + 2m*π, con m ∈ Z (en el primer cuadrante),

    x = 7π/6 + 2n*π, con n ∈ Z (en el tercer cuadrante);

    b)

    tanx = - √(1/3), que corresponde a ángulos del segundo y del cuarto cuadrante, cuyas expresiones generales son:

    x = 5π/6 + 2p*π, con p ∈ Z (en el primer cuadrante),

    x = 11π/6 + 2q*π, con q ∈ Z (en el tercer cuadrante).

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    leire
    el 18/3/17

    El seno del ángulo doble no es 2·sen·cos? Tú has puesto sen·cos, al principio :)

    Gracias por la ayuda!

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Lucía Sánchez
    el 18/3/17

    Hola, alguien me ayudaría a representar estar función gráficamente?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/3/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    ngb
    el 18/3/17

    Hola, no sé resolver este límite, a mi me da cero y tiene que dar ➕ infinito 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/3/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    ngb
    el 18/3/17

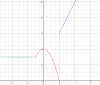
    Hola, en esta función me salen 3 asintotas verticales en los puntos donde la función no existe, es decir, x=0  x=-1  x=2   y una asintotas horizontal en y=0. La función no es continua y las discontinuidades que presenta son inevitables de tipo asintotas. Si lo dicho es correcto, no entiendo que es lo que tengo que hacer en el apartado C y E. 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 18/3/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Nuria
    el 18/3/17

    Muchísimas gracias, ahora lo entiendo perfectamente

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Antonius Benedictus
    el 18/3/17

    PARA ABRIL:


    reply•thumb_up•0 voto/s•flag
    icon

    Soporte unicoos
    el 12/4/17

    Perfecto profe!

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo