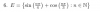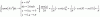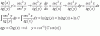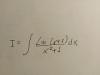-
Alguien podria explicarme bien lo de integrales con fracciones simples? Siempre se me complica en la hora de bucar A y B necesito q me explique buen paso por paso porq n logro de entender.... dejo un ejercicio bq estoy segura q n lo hice bien


gonzalezlbl
el 27/1/20No vi de dónde sacaste que A = 0. Lo cierto es que A = -½ . Vamos a continuar desde el punto donde llegaste a la siguiente expresión:
1 = A(x-1) + B(x+1) (expresión 1)
Desarrollaste el segundo miembro como sigue:
1 = Ax - A + Bx + B
Asociando términos semejantes; es decir, x con las x, y términos independientes con términos independientes:
1 = (A+B)x + (-A+B) o también lo podemos escribir así: 0x + 1 = (A+B)x + (-A+B)
Por igualdad de polinomios, el primer miembro debe ser igual al segundo, entonces en el segundo miembro el coeficiente de x debe ser cero: A+B = 0
Asimismo, los términos independientes deben ser iguales: 1 = -A + B
Tenemos así estas dos ecuaciones:
A + B = 0 (ecuación 1)
-A + B = 1 (ecuación 2)
Sumando miembro a miembro ambas ecuaciones, resulta 2B = 1
Así, B = ½
Sustituyendo este resultado en la ecuación 1: A + ½ = 0
Despejando nos queda A = -½
----------------------------------------------------------------
Otra forma más fácil de resolver esto:
Partiendo de la expresión 1: 1 = A(x-1) + B(x+1)
Como esto debe cumplirse para cualquier valor de x, hagamos x = 1 para que desaparezca el término donde está A:
1 = A(1-1) + B(1+1)
1 = 2B
B = ½
Luego, para que desaparezca B, hacemos x = -1 :
1 = A(-1-1) + B(-1+1)
1 = -2A
A = -½
-
Ayudenme con este ejercicio!!! Por favor!!! No lo he podido resolver.
Determine una aproximación cubica f(x,y)= Ln2(3x-5y+1) alrededor del punto x0 , y0 = (1, -1)


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)


Antonio Silvio Palmitano
el 27/1/20Tienes la expresión de la función:
f(x,y) = Ln2(3x - 5y + 1), que evaluada en el punto en estudio: P0(1,-1) queda: f(1,-1) = Ln2(9).
Luego, planteas las expresiones de las funciones derivadas parciales primeras (observa que debes aplicar la Regla de la Cadena), y queda:
fx(x,y) = 6*Ln(3x - 5y + 1), que evaluada en el punto en estudio: P0(1,-1) queda: fx(1,-1) = 6*Ln(9),
fy(x,y) = -10*Ln(3x - 5y + 1), que evaluada en el punto en estudio: P0(1,-1) queda: fy(1,-1) = -10*Ln(9).
Luego, planteas las expresiones de las funciones derivadas parciales segundas (observa que debes aplicar la Regla de la Cadena), y queda:
fxx(x,y) = 18/(3x - 5y + 1), que evaluada en el punto en estudio: P0(1,-1) queda: fxx(1,-1) = 2,
fxy(x,y) = fyx(x,y) = -30/(3x - 5y + 1), que evaluadas en el punto en estudio: P0(1,-1) queda: fxy(1,-1) = fyx(1,-1) = -10/3,
fyy(x,y) = 50/(3x - 5y + 1), que evaluada en el punto en estudio: P0(1,-1) queda: fyy(1,-1) = 50/9.
Luego, planteas las expresiones de las funciones derivadas parciales terceras (observa que debes aplicar la Regla de la Cadena), y queda:
fxxx(x,y) = -54/(3x - 5y + 1)2, que evaluada en el punto en estudio: P0(1,-1) queda: fxxx(1,-1) = -2/3,
fxxy(x,y) = fxyx(x,y) = fyxx(x,y) = 90/(3x - 5y + 1)2, que evaluadas en el punto en estudio: P0(1,-1) queda: fxxy(1,-1) = fxyx(1,-1) = fyxx(1,-1) = 10/9,
fxyy(x,y) = fyxy(x,y) = fyyx(x,y) = -150*/(3x - 5y + 1)2, que evaluadas en el punto en estudio: P0(1,-1) queda: fxyy(1,-1) = fyxy(1,-1) = fyyx(1,-1) = -50/3,
fyyy(x,y) = 250*Ln(3x - 5y + 1)2, que evaluada en el punto en estudio: P0(1,-1) queda: fyyy(1,-1) = 250/9.
Luego, planteas el desarrollo de Taylor general de orden tres de una función (observa que tienes que las derivadas parciales "cruzadas" segundas y terceras son continuas, por lo que tienes que sus expresiones son iguales), y queda:
T3(x,y) =
= f(x0,y0) +
+ fx(x0,y0)*(x - x0) + fy(x0,y0)*(y - y0) +
+ (1/2!)*( fxx(x0,y0)*(x - x0)2 + 2*fxy(x0,y0)*(x - x0)*(y - y0) + fyy(x0,y0)*(y - y0)2 ) +
+ (1/3!)*( fxxx(x0,y0)*(x - x0)3 + 3*fxxy(x0,y0)*(x - x0)2*(y - y0) + 3*fxyy(x0,y0)*(x - x0)*(y - y0)2 + fyyy(x0,y0)*(y - y0)3 );
luego, reemplazas los valores de las coordenadas del punto en estudio: x0 = 1, y0 = -1, resuelves signos en los segundos términos de los binomios, y queda:
T3(1,-1) =
= f(1,-1) +
+ fx(1,-1)*(x - 1) + fy(1,-1)*(y + 1) +
+ (1/2!)*( fxx(1,-1)*(x - 1)2 + 2*fxy(1,-1)*(x - 1)*(y + 1) + fyy(1,-1)*(y + 1)2 ) +
+ (1/3!)*( fxxx(1,-1)*(x - 1)3 + 3*fxxy(1,-1)*(x - 1)2*(y + 1) + 3*fxyy(1,-1)*(x - 1)*(y + 1)2 + fyyy(1,-1)*(y + 1)3 );
luego, reemplazas los valores de la función y de sus derivadas parciales primeras, segundas y terceras evaluadas en el punto en estudio, y queda:
T3(1,-1) =
= Ln2(9) +
+ 6*Ln(9)*(x - 1) - 10*Ln(9)*(y + 1) +
+ (1/2!)*( 2*(x - 1)2 + 2*(-10/3)*(x - 1)*(y + 1) + (50/9)*(y + 1)2 ) +
+ (1/3!)*( -(2/3)*(x - 1)3 + 3*(10/9)*(x - 1)2*(y + 1) - (50/3)*(x - 1)*(y + 1)2 + (250/9)*(y + 1)3 ).
Espero haberte ayudado.
-
Chicos respecto a este ejercicio....
La derivada de y respecto a z, seria así???
De no ser así corrijanme por favor!!


Antonio Silvio Palmitano
el 27/1/20Vamos con una orientación.
Observa que la expresión de la función de dos variables de tu enunciado es logarítmica, por lo que aplicas la propiedad del logaritmo de una división de funciones, y queda (observa que escribimos a las raíces cuadradas como potencias):
Z = Ln(x - [x2+y2]1/2) - Ln(x + [x2+y2]1/2);
luego, derivas término a término (observa que debes aplicar la Regla de la Cadena en ambos términos), y las expresiones de las funciones derivadas parciales primeras quedan:
Zx = [ 1/(x - [x2+y2]1/2) ]*( 1 - x*[x2+y2]-1/2 ) - [ 1/(x + [x2+y2]1/2) ]*( 1 + x*[x2+y2]-1/2 ),
Zy = [ 1/(x - [x2+y2]1/2) ]*( -y*[x2+y2]-1/2 ) - [ 1/(x + [x2+y2]1/2) ]*( y*[x2+y2]-1/2 ).
Luego, puedes aplicar la propiedad de las potencias con exponentes negativos, y también la propiedad de las potencias fraccionarias para escribirlas como raíces, y luego operar a fin de reducir las expresiones (te dejo la tarea).
Espero haberte ayudado.
-
El segundo ej lo tengo hecho, pero el primero y el tercero hay algo que se me resiste.
Del primero saco que la pendiente de la recta buscada es 3, y también que el producto de los vectores AB*AC=60 u2, y ya no saco más.
-

David
el 27/1/20https://edu.gcfglobal.org/es/fraccionarios/fracciones-negativas-y-con-signos/1/
A ver si este link te ayuda a resolver tu duda.