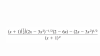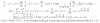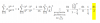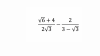logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    María
    el 13/2/17

    Ayuda con este ejercicio. 


    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 13/2/17

    María ¿Qué necesitas?

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Marcos
    el 14/2/17

    Hola María. No se que necesitas resolver. Yo supongo que saber el valor de x. 

    Acá te lo explica paso a paso y esta muy claro. Espero haberte ayudado


    https://www.symbolab.com/solver/step-by-step/%5Cfrac%7B%5Cleft(x%2B1%5Cright)%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5Cleft(2x-3x%5E%7B2%7D%5Cright)%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%5Cleft(2-6x%5Cright)-%5Cleft(2x-3x%5E%7B2%7D%5Cright)%5E%7B%5Cfrac%7B1%7D%7B2%7D%7D%7D%7B%5Cleft(x%2B1%5Cright)%5E%7B2%7D%7D%3D0



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Ángel
    el 14/2/17

    Para saber el valor de x basta con saber qué valor/es anula/n el denominador, en este caso, -1


    Entonces el valor de x puede ser cualquiera, excepto -1


    Si es una ecuación, pon la otra parte de la igualdad para que podamos ayudarte

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    lbp_14
    el 13/2/17

    Hola Unicoos, cómo cálculo el cos (u,v)? Mi profesora define la proyección de un vector como |u|•cos(u,v) 

    Tengo examen mañana.

    Muchas GRACIAS 


    reply•thumb_up•0 voto/s•flag
    icon

    Nico Rueda
    el 13/2/17

    Hola! Justamente nosotros nos saltamos esta parte del tema de vectores (a proyecciones me refiero). Pero creo que te podré ayudar, para calcular el cos de u,v tienes que usar la siguiente formula :

    cos α = (u·v)/|u|·|v|

    Tendrás que usar la función de cos-1 de la calculadora, espero haberme explicado!

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    lbp_14
    el 13/2/17

    Efectivamente, ya me salen los ejercicios. Muchas gracias! 

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Javi
    el 13/2/17
    flag


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 14/2/17

    Establecemos un sistema de referencia con un eje vertical, positivo hacia arriba, con origen al nivel del mar, y expresamos el tiempo en minutos y las posiciones en metros.

    Luego, tenemos que la altura inicial (para t = 0) es y = 5, y a partir del enunciado tenemos la ecuación de movimiento (observa que la variable t toma valores estrictamente positivos):

    y(t) = at2 + bt + c, donde a, b y c son números reales a determinar;

    evaluamos para t = 0:

    y(0) = c = 5;

    evaluamos para t = 1:

    y(1) = a*12 + b*1 + c = 10, resolvemos términos y queda: a + b + c = 10;

    evaluamos para t = 2:

    y(2) = a*22 + b*2 + c = 5, resolvemos términos y queda: 4a + 2b + c = 5.

    Luego, con las tres ecuaciones remarcadas tenemos el sistema:

    c = 5

    a + b + c = 10

    4a + 2b + c = 5

    reemplazamos el valor de c en las dos últimas ecuaciones, hacemos pasajes de términos y queda:

    a + b = 5

    4a + 2b = 0, de aquí despejamos: b = - 2a (1),

    sustituimos en la primera ecuación y queda:

    - a = 5, de aquí despejamos:  a = - 5,

    reemplazamos en la ecuación señalada (1) y queda: b = 10.

    Luego, reemplazamos en la ecuación de movimiento y queda:

    y(t) = - 5t2 + 10t + 5.

    Luego, si entendemos que el tiempo de vuelo comienza con el lanzamiento del cuerpo y termina cuando llega al agua, planteamos:

    y(t) = 0, sustituimos y queda:

    - 5t2 + 10t + 5 = 0, dividimos por -5 en todos los términos de la ecuación y queda:

    t2 - 2t - 1 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

    1) t = 1 - √(2) ≅ - 0,41, que no tiene sentido para este problema;

    2) t = 1 + √(2) ≅ 2,41 (en minutos, que es el tiempo que transcurre desde el lanzamiento del cuerpo hasta su llegada al agua).

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Zatin
    el 13/2/17
    flag

    Alguien sabe algún vídeo donde se explique discontinuidades de funciones con saltos de valor n?


    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 19/2/17

    ¿de valor n?... De salto finito?...
    En esta leccion... Funcion a trozos Discontinuidad 01

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    José Alfaro Cruz
    el 13/2/17

    hola alguien sabe como hacer  senα=cosα? porfa nivel de 4 de ESO


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 13/2/17

    Recuerda la identidad trigonométrica: sena = √(1 - cos2a), luego sustituyes en la ecuación del enunciado y queda:

    √(1 - cos2a) = cosa, haces pasaje de raíz como potencia y queda:

    1 - cos2a = cos2a, haces pasajes de términos y queda:

    - 2cos2a = - 1, haces pasaje de factor como divisor y queda:

    cos2a = 1/2, haces pasaje de potencia como raíz y tienes dos opciones:

    1) cosa = 1/√(2), al que corresponde: sena = 1/√(2), que corresponde al valor angular: a = 45°;

    2) cosa = -1/√(2), al que corresponde: sena = -1/√(2), que corresponde al valor angular: a = 225°.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    María
    el 13/2/17


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/2/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Mel Alarcón
    el 13/2/17

    ayuda con estos ejercicios! no me salen


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/2/17


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonius Benedictus
    el 13/2/17


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonius Benedictus
    el 13/2/17


    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Matias Benditkis
    el 13/2/17

    Como resuelvo el sistema de ecuaciones del punto e) por alguno de los métodos ?




    reply•thumb_up•0 voto/s•flag
    icon

    Javi
    el 13/2/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Paula
    el 13/2/17

    Ayuda con este ejercicio, Antonio Benito, ¡por favor!. Paso a paso. Gracias de antemano.


    reply•thumb_up•0 voto/s•flag
    icon

    Alexis de Barros
    el 13/2/17

    aqui puedes verlo paso a paso espero que te sirva https://es.symbolab.com/solver/derivative-calculator/%5Cfrac%7B%5Csqrt%7B6%7D%2B4%7D%7B2%5Csqrt%7B3%7D%7D-%5Cfrac%7B2%7D%7B3-%5Csqrt%7B3%7D%7D


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Soraya
    el 13/2/17

    Buenas tardes , podrían ayudarme con el ejercicio 4 , muchas gracias 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 13/2/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    suficiente