-
alguien que sepa resolverme este limite por favor, es que lo he intentado de varias formas, y no se hacerlo, en teoria hay que poner: e^1/x / 1/x^2 para que te quede infinito entre infinito, y ya aplicar l'hopital pero no se como hacerlo :v



Antonio Silvio Palmitano
el 10/2/17Observa que el primer factor tiende a cero y que el segundo tiende a +infinito, por lo que el límite es indeterminado.
Puedes plantear la sustitución (cambio de variable):
w = 1/x, de donde tienes: x = 1/w, y observa que w tiende a +infinito cuando x tiende a 0 por la derecha.
Luego sustituyes y el límite queda:
Lím(w→+∞) (1/w2)ew = Lím(w→+∞) ew/w2 = observa que el numerador y el denominador tienden ambos a +infinito,
aplicas la Regla de L'Hôpital (recuerda que derivamos independientemente al numerador y al denominador):
= Lím(w→+∞) ew/ 2w = observa que el numerador y el denominador tienden ambos a +infinito,
volvemos a aplicar la regla:
= Lím(w→+∞) ew/ 2 = +∞.
Espero haberte ayudado.
-
hola tengo una duda como puedo simplificar esa expresión trigonométrica √(1-sen (x))/(1+sen(x))


Antonio Silvio Palmitano
el 10/2/17Tienes el argumento de la raíz:
(1 - senx)/(1 + senx) = multiplicas al numerador y al denominador por (1 - senx) y queda:
= (1 - senx)(1 - senx) / (1 + senx)(1 - senx) ) = desarrollamos el denominador (observa que tenemos cancelaciones) y queda:
= (1 - senx)2 / (1 - sen2x) = aplicamos la identidad trigonométrica del coseno en función del seno en el denominador y queda:
= (1 - senx)2 / cos2x = asociamos potencias y queda:
= ( (1 - senx)/cosx )2.
Luego, pasamos a la expresión de tu enunciado:
√(1-sen (x))/(1+sen(x)) = sustituimos = √( ( (1 - senx)/cosx )2 ) = simplificamos índice y exponente = (1 - senx)/cosx.
Espero haberte ayudado.
-
Ayuda!!!
Considere el campo
f(x,y) = ( xy^2)/x^2+y^4 si x=0
f(0,y)=0
obtenga la siguiente derivada de f: f’(
, y)
Encontre que la funcion no es diferenciable en (0,0)


David
el 19/2/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
alguien me puede ayudar a demostrar esta propiedad
usando las propiedades basicas del producto escalar
de antemano muchas gracias


Antonio Silvio Palmitano
el 10/2/17Consideramos los vectores con componentes reales: u = <a,b,c> y v = <x,y,z>, y el número real λ.
Planteamos:
λ(u•v) = sustituimos = λ(<a,b,c>•<x,y,z>) = desarrollamos el producto escalar = λ(ax + by + cz) = distribuimos = λax + λby + λcz = asociamos factores en los términos:
= (λa)x + (λb)y + (λc)z = expresamos como producto escalar entre dos vectores = <λa,λb,λc>•<x,y,z> = extraemos el factor escalar en el primer vector:
= (λ<a,b,c>)•<x,y,z> = sustituimos = (λu)•v.
Espero haberte ayudado.
-
Sabiendo que sen x = -2/3 y cos x < 0, calcula, sin hallar x, el valor de:
cos(π +x)

Antonio Silvio Palmitano
el 9/2/17Planteamos la identidad pitagórica fundamental:
sen2x + cos2x = 1, reemplazamos el valor del seno, resolvemos su término y queda:
4/9 + cos2x = 1, hacemos pasaje de término y queda:
cos2x = 5/9, hacemos pasaje de potencia como raíz (recuerda que el coseno es negativo según el enunciado) y queda:
cosx = - √(5/9) = - √(5)/3.
Luego, pasamos al ejercicio:
cos(π + x) = aplicamos la identidad del coseno de la suma de dos ángulos:
= cosπ*cosx - senπ*senx = reemplazamos valores:
= (-1)*(- √(5)/3) - (0)*(-2/3) = resolvemos términos:
= √(5)/3 + 0 = √(5)/3.
Espero haberte ayudado.
-
Sabiendo que sen x = -2/3 y cos x < 0, calcula, sin hallar x, el valor de:
sen(π −x)


Antonio Silvio Palmitano
el 9/2/17El planteo y los cálculos son muy parecidos al ejercicio que enviaste más arriba, y la identidad trigonométrica que debes emplear es la que corresponde al seno de la resta entre dos ángulos:
sen(π - x) = senπ*cosx - cosπ*senx.
Haz el intento de terminar la tarea, y si te es preciso no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola, tengo una duda de universidad pero bastante elemental, que a veces me agarra la duda.
Es lo siguiente:
Si tengo que derivar la función 1/x se que tengo que hacer
((1)' * (x) - (1)*(x)') / x2.
Pero mi duda es la siguente: ese termino del denominador que se eleva al cuadrado. Si tengo por ejemplo (7-x)4 en el denominador. ¿Derivado, va (7-x)5 o (7-x)8 , o ninguno ?
Desde ya muchas gracias


Antonio Silvio Palmitano
el 9/2/17Recuerda la Regla de Derivación para un cociente de la forma y = u/v:
y ' = ( u ´* v - u* v ' ) / v2.
Luego, vamos con dos ejemplos:
1)
y = 1/x,
luego, tienes:
u = 1, cuya derivada queda: u ' = 0,
v = x, cuya derivada queda: v ' = 1;
luego aplicas la regla y queda:
y ' = ( u ´* v - u* v ' ) / v2 = sustituyes = (0*x - 1*1)/x2 = (0 - 1)/x2= -1/x2.
2)
y = x3/(7 - x)4,
luego tienes:
u = x3, cuya derivada queda: u ' = 3x2,
v = (7 - x)4, cuya derivada queda: v ' = 4*(7 - x)3*(-1) = - 4*(7 - x)3;
luego aplicas la regla y queda:
y ' = ( u ´* v - u* v ' ) / v2 = sustituyes = ( 3x2*(7 - x)4 - x3*(-4)*(7 - x)3 ) / ( (7 - x)4 )2= ( 3x2*(7 - x)4 + 4*x3*(7 - x)3 ) / (7 - x)8.
Observa que puedes extraer factores comunes en el numerador de la expresión de la derivada y luego puedes simplificar (haz el intento de llevar la expresión a su forma más sencilla posible).
Como sugerencia, es muy conveniente plantear primero las derivadas del numerador y del denominador, para luego sustituir en la expresión general de la derivada de un cociente entre dos funciones.
Espero haberte ayudado.
-
Hola Unicoos! Hice este ejercicio de Continuidad y Derivabilidad de las 2 formas. La forma corta y la forma larga, y me da un resultado distinto cuando tendrían que ser iguales. Sólo es igual el "-4". Lo releí varias veces y no puedo encontrar el error. Me pueden ayudar? Gracias!




Antonio Silvio Palmitano
el 9/2/17Vamos a investigar la existencia o no existencia de la función derivada en x = 0 según la definición ("forma larga"), y para ello planteamos los límites laterales del cociente incremental.
f-' (0) = Lím(h→0-) ( f(0+h) - f(0) )/h = Lím(h→0-) ( f(h) - f(0) )/h = sustituimos:
= Lím(h→0-) ( (2h2 + 2h) - (0) )/h = resolvemos y factorizamos el argumento:
= Lím(h→0-) h(2h+2)/h = simplificamos:
= Lím(h→0-) (2h+2) = 0 + 2 = 2;
f+' (0) = Lím(h→0+) ( f(0+h) - f(0) )/h = Lím(h→0+) ( f(h) - f(0) )/h = sustituimos:
= Lím(h→0+) ( (4h2 - 4h) - (0) )/h = resolvemos y factorizamos el argumento:
= Lím(h→0-) h(4h-4)/h = simplificamos:
= Lím(h→0-) (4h-4) = 0 - 4 = - 4.
Como puedes ver, los resultados coinciden con los que obtuviste al emplear la "forma corta",
y puedes concluir que la función no es derivable en x = 0, ya que sus derivadas laterales no coinciden.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 10/2/17Para el tipo de función a trozos, en que cada trozo es polinómico, la forma corta sirve. y se la acepta como válida. Pero si hablamos de otros tipos de funciones, hay casos en que no es así.
Y siempre debes considerar que la forma estricta consiste en aplicar la definición (la "forma larga").
Espero haberte ayudado.












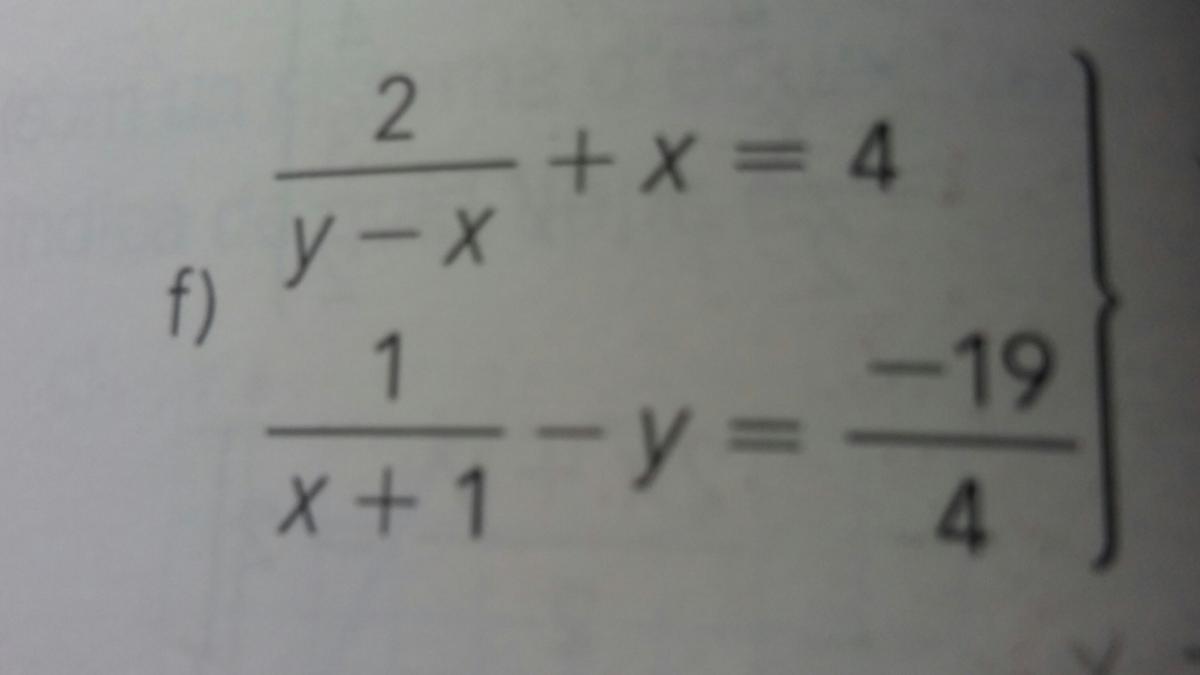 alguien me podria ayudar a resolver este sistemas de ecuaciones?:
alguien me podria ayudar a resolver este sistemas de ecuaciones?:



