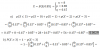logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    pablo
    el 26/12/16

    Hola me podrían decir que error cometí al hallar el espacio propio del autovalor λ=10, ya que estoy obteniendo como resultado el nulo 


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Te has equivocado al reemplazar el autovalor en los dos últimos elementos de la diagonal principal de la matriz, observa que son: -8, -5 y - 5 (has consignado -3 en los dos últimos).

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Ibán Sinube
    el 26/12/16

    Se trata de:

    Si para todo x se cumple que 1=ax^2+(bx+c)(x-1), entonces:

    a) c+a+2b=0

    b) a+b+2c=0

    c)...

    d)...

    Desarrollando el polinomio queda un coeficiente para x^2, otro para x y un término independiente:

    1=(a+b)x^2 + (b+c)x + c

    Se igualan a 0 los coeficientes y se suman. El resultado es la opción a, que es la correcta, por lo visto. Mi duda es que no se qué sentido tiene hacer eso. ¿Podrías clarificar este procedimiento? Yo entiendo que dadas las soluciones igualadas a 0,  bueno me da una pista para igualar los coeficientes a 0, pero que pasa con el término independiente, que sería c-1, este no interviene, ¿por qué? Gracias.


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Si desarrollas el segundo miembro, la ecuación del enunciado queda:

    1 = ax2 + bx2 - bx + cx - c, luego extraes factor común por grupos y queda:

    1 = (a + b)x2 + (-b + c)x - c, luego, observa que tienes una igualdad entre polinomios, y el primer miembro puedes escribirlo:

    0x2 + 0x + 1 = (a + b)x2 + (-b + c)x - c, luego, por igualdad entre polinomios, igualas término a término según el grado y queda:

    0x2 = (a + b)x2

    0x = (-b + c)x

    1 = -c,

    luego comparas coeficientes y queda el sistema de ecuaciones:

    0 = a + b

    0 = -b + c

    1 = -c, haces pasaje de término y queda: c = -1,

    reemplazas en las otras ecuaciones (en realidad, solo en la segunda) y queda:

    0 = a + b

    0 = -b - 1, haces pasaje de término y queda: b = -1,

    reemplazamos en la ecuación restante y queda:

    0 = a - 1, hacemos pasaje de término y queda: 1 = a.

    Para verificar, reemplazas en la ecuación original y queda:

    1 = 1x2 + (-1x - 1)(x - 1),

    luego puedes desarrollar el segundo miembro y verás que se verifica la solución hallada: a = 1, b = -1, c = -1.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos
    el 25/12/16

    Consulta en la b, a que se refiere con menor dispercion ?


    reply•thumb_up•0 voto/s•flag
    icon

    Ibán Sinube
    el 26/12/16

    Yo usaría la varianza y si no me clarifica la dispersión, uso la desviación típica que es la raíz positiva de la varianza. Cuanto mayor sea la desviación típica, más dispersos serán los datos, es decir, más alejados estarán de la media.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos
    el 25/12/16

    Este ejercicio esta bueno? Distribución binomial 



    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 26/12/16

    Parece que sí:


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos Ojeda
    el 25/12/16

    Hola, tengo el siguiente ejercicio de ecuaciones diferenciales:


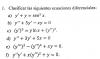
    yo lo intenté hacer:


    a) Ecuación diferencial de variables separables

    b) Ecuación diferencial lineal homogénea orden 2

    c) Ecuación diferencial lineal homogénea orden 2

    d) Ecuación diferencial lineal homogénea orden 2

    e) Ecuación diferencial lineal homogénea orden 3

    f) Ecuación diferencial lineal homogénea orden 2


    ¿lo tengo bien?




    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 25/12/16

    Tienes ecuaciones lineales excepto la última, y recuerda que el orden lo tienes con la mayor derivada, y que el grado lo tienes con la potencia a la que está elevada la mayor derivada, y también recuerda que puedes clasificar con coeficientes constantes, coeficientes variables, homogéneas y no homogéneas.

    a) Ecuación diferencial lineal, de orden 1, grado 1, coeficientes constantes no homogénea.

    b) Ecuación diferencial lineal homogénea orden 2, grado 1, coeficientes variables.

    c) Ecuación diferencial lineal homogénea orden 2, grado 2, coeficientes variables.

    d) Ecuación diferencial lineal no homogénea orden 2, grado 1, coeficientes constantes.

    e) Ecuación diferencial lineal homogénea orden 3, grado 2, coeficientes variables.

    f) Ecuación diferencial no lineal homogénea orden 2, grado 2, coeficientes variables.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carlos Ojeda
    el 27/12/16

    Gracias

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Enrique H.M
    el 25/12/16

    Buenas noches.


    Mi duda es, ¿por qué la transformada inversa de (3s)/(s^2-9) es 3/2 (e^3t+e^-3t) en lugar de 3 cos 3t? ¿Al realizar la inversa no puedo sacar la constante fuera? ¡Muchas gracias y que tengan todos felices fiestas!

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Observa que la transformada de la función:

    f(t) = 3cos(3t) queda: F(s) = 3s/(s2 + 9).

    Y observa que la transformada de la función:

    g(t) = 3cosh(3t) = (3/2)(e3t + e-3t) queda: G(s) = 3s/(s2 - 9).

    Observa que los denominadores de las expresiones de las transformadas no son iguales.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Enrique H.M
    el 26/12/16

    Muchas gracias por su tiempo. ¿Debo hacer siempre la comprobación de la transformada o es necesario seguir alguna prioridad a la hora de realizar la inversa de Laplace para evitar estos errores?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Es conveniente verificar bien las expresiones, tanto de las transformadas como de las antitransformadas. No me parece necesario, a no ser que te lo pidan explícitamente en un ejercicio, qu ese haga el planteo completo, pero sí es conveniente tener las tablas de transformadas y antitransformadas a mano y consultarlas para verificar soluciones.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos
    el 25/12/16

    Hola este ejercicio esta bueno? es de probabilidad condicionada....



    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 26/12/16

    El apartado b) , no:


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos
    el 25/12/16

    Hola, me pueden ayudar con este ejercicio en la a me dio 1 y en la b 2 imposible que me de eso. felices fiestas ;) 



    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Tienes la variable aleatoria X: "calificación obtenida en la capacitación", con distribución normal, con media: μ = 65, y desviación típica: σ = 15,

    llamamos Z a la distribución normal estándar, con media: μ = 0, y desviación típica: σ = 1).

    a) p(X ≥ 80) = p( (X-65)/15 ≥ (80-65)/15 ) = p(Z ≥ 1) = buscas en la tabla.

    b) p(X ≥ 50) = p( (X-65)/15 ≥ (50-65)/15 ) = p(Z ≥ -1) = buscas en la tabla.

    c) Llamemos p = p(X < 50) = p( (X-65)/15 < (50-65)/15) ) = p(Z < -1) = buscas en la tabla (probabilidad de que el empleado elegido sea enviado a un nuevo curso);

    q = 1 - p (probabilidad de que el empleado elegido no sea enviado a un nuevo curso).

    Tienes una distribución binomial con parámetros n = 5 y probabilidad favorable p, para la variable aleatoria: Y: "cantidad de empleados enviados a un nuevo curso".

    Luego planteamos:

    p(Y = 3) = C(5,3)p3q2 = 10p3q2 = te dejo los cálculos.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carlos
    el 26/12/16

    Muchas gracias puedo hacerle otra consulta profesor, en un ejercicio que me pidan media y desviación típica y me den el valor de x y el = como puedo saber si el valor de = tengo que de transformarlo de la tabla o no, 

    por ejemplo me dan P(X≤2)=0,2 y P(X≤3)=0,3

    entonces debo hacer el sistema pero antes de eso debo como saber si esos 0,2 y 0,3 de transformarlos de la tabla...


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Observa que tienes dos ecuaciones, y que las incógnitas son μ (media) y σ (desviación típica. 

    Llamamos Z a la variable aleatoria con distribución normal, media cero y desviación típica 1.

    Luego, vamos con las ecuaciones:

    p(X ≤ 2) = p( (X-μ)/σ  ≤ (2-μ)/σ ) = p( Z ≤ (2-μ)/σ ) = 0,2 (1)

    p(X ≤ 3) = p( (X-μ)/σ  ≤ (3-μ)/σ ) = p( Z ≤ (3-μ)/σ ) = 0,3 (2)

    Luego, como tenemos los valores de las dos probabilidades, buscamos "adentro" de la tabla:

    para la probabilidad señalada (1) buscamos: 0,20000, y nos queda: z = -0,84;

    para la probabilidad señalada (2) buscamos 0,300000, y nos queda: z =  -0,53.

    Luego, planteamos a partir de los argumentos correspondientes el sistema de ecuaciones::

    (2-μ)/σ = -0,84

    (3-μ)/σ = -0,53

    hacemos pasajes de divisores como factores y queda:

    2 - μ = -0,84σ

    3 - μ = -0,53σ

    luego restamos miembro a miembro y queda:

    - 1 = -0,31σ, hacemos pasaje de factor como divisor y queda: 3,23 = σ,

    luego reemplazamos en la primera ecuación y queda:

    2 - μ = -0,84*3,23, resolvemos el segundo miembro, hacemos pasajes de términos y queda: 4,71 = μ,

    y puedes verificar el resultado en la segunda ecuación.

    Espero haberte ayudado.








    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Pablo Reyes
    el 25/12/16

    Hola.

    Cual es el dominio de la función : f(x) = x2 / 1 + valor absoluto de X. 

    1º SEPARO LA FUNCIÓN, porque siempre que haya una función con valor absluto me piden que la estudie cuando sea NEGATIVO y cuando sea POSITIVO.

    Bien:


    Cuando x2  / x + 1      le corresponde el intervalo (-∞, -1) U (1, ∞) 

    y cuando  x2  / 1 - x le corresponde el intervalo (-1,1)


    ¿ES ESTO CORRECTO O LO HE HECHO MAL?


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 26/12/16

    Si la expresión de la función es: f(x)= x2/(1 + |x|), 

    observa que el denominador está constituido por dos términos positivos, y que toma valores mayores o iguales que 1,

    por lo tanto, tienes que el denominador nunca toma el valor cero, y, por lo tanto, el dominio de la función queda:

    D = (-∞,+∞) = R.

    Luego, a partir de la definición de valor absoluto (|x| = x, si x ≥ 0, o |x| = -x, si x < 0), puedes expresar la función con trozos y queda:

    f(x) =

    x2/(1 + x)               si x ∈ [0,+∞)

    x2/(1 - x)                si x ∈ (-∞,0)

    observa que los denominadores no toman el valor cero en los intervalos correspondientes.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Rosario Drysis
    el 26/12/16

    El dominio son todos los reales. La x está dentro del valor absoluto. Por definición si tu x vale -1  , el valor absoluto la convierte en uno positivo

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Pablo Reyes
    el 25/12/16

    Hola.

    Cual es el dominio de la función : f(x) = x2 / 1 + valor absoluto de X

    Hay que separar la función para cuando el valor sea positivo y negativo pero no sé determinar con certeza el dominio. Una ayuda por favor.

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 25/12/16

    1+/x/ =0→/x/=-1 (imposible)

    Dom(f)=R

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Pablo Reyes
    el 25/12/16

    Ya pero me piden que separe la funcion cuando sea menos x y cuando sea x positiva

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonius Benedictus
    el 25/12/16

    f(x)=

    =x2/(1-x)  ,si x<0

    =x2/(1+x), si x≥0



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo