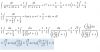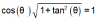logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Carlos Ojeda
    el 29/11/16

    Hola, ¿me podrían decir cómo se hace la primera integral sustituyendo las fórmulas trigonométricas que que empleo en la segunda? Y en la segunda, otra más en la que me quedo atascado y nada, no llego a la solución. Gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 29/11/16

    Las expresiones que empleaste en el ejercicio anterior, son aplicables cuando tienes argumentos con factores  de la forma (1-cosx) o (1+cosx), entre otros casos.

    En el ejercicio de la parte superior, debes plantear la sustitución: x = w2, de donde tienes: dx = 2w*dw, luego sustituyes y la integral queda:

    I = ∫ senw*2w*dw = 2 ∫ w*senw*dw, que puedes continuar planteando el método de integración por partes.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Big master
    el 29/11/16

    Me pueden ayudar con  este problema  

    "Un banco lanza al mercado un plan de inversión cuya rentabilidad R(x), en pesos, viene dada en función de la cantidad invertida, x en pesos, por medio de la expresión : R(x)= -0.001x^2 + 0.4x + 3.5 . Deducir que cantidad de dinero convendrá invertir en dicho plan. ¿Qué rentabilidad obtuvo el caso anterior?    


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 29/11/16

    Observa que x puede tomar valores positivos solamente.

    Luego, planteamos la derivada de la funciión:

    R ' (x) = -0,002x + 0,4.

    Luego, planteamos la condición de punto crítico (posible máximo o mínimo de la función):

    R ' (x) = 0, sustituimos y queda:

    -0,002x + 0,4 = 0, hacemos pasaje de término, luego de factor como divisor y queda:

    x = (-0,4)/(-0,002), resolvemos y llegamos a:

    x = 200.

    Luego, evaluamos la función para el punto crítico, y para dos valores cercanos a él, uno mayor y otro menor:

    para x = 190 tenemos: R(190) = 43,4;

    para x = 200 tenemos: R(200) = 43,5;

    para x = 210 tenemos: R(210) = 43,4.

    Luego, concluimos que si se invierte x = 200, se obtendrá la renta máxima: R(200) = 43,5.

    Otra forma para plantear el problema, es encontrar las coordenadas del vértice de la parábola, que es la gráfica de la función.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carlos Ojeda
    el 29/11/16

    Bueno, tampo me sale esta, no sé cómo terminarlas,las tengo que hacer exclusivamente con las fórmulas trigonométricas. Gracias


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 29/11/16

    Tienes la integral:

    I = ∫ ( senx*cosx/(1-cosx) )dx,

    aplicas la sustitución (cambio de variable): w = cosx, de donde tienes: dw = -senxdx, y también tienes: -dw = senxdx, sustituyes y queda:

    I = ∫ ( w/(1-w) )*(-dw),

    luego observa que la expresión del integrando puede escribirse: w/(1-w) = ( (w-1) + 1 )/(1-w) = (w-1)/(1-w) + 1/(1-w) = -1 - 1/(w-1), sustituyes y queda:

    I = ∫ ( -1 - 1/(w-1) )*(-dw) = ∫ ( 1 + 1/(w-1) )*dw, resolvemos y queda:

    I = w + ln|w-1| + C, sustituimos la expresión para w y llegamos a:

    I = cosx + ln|cosx - 1| + C.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carlos Ojeda
    el 29/11/16

    Hola Antonio,por indicaciones del profesorado, solo puedo sustituir usando las fórmulas trigonométricas que empleo en las integrales. Gracias


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Gisela Torres
    el 29/11/16

    Buenas noches,

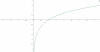
    he estado estudiando logaritmos y entre los videos no he visto ninguno que muestre cómo representarlos gráficamente. Me sería de gran ayuda para entenderlo mejor, ya que hay algunos ejercicios que directamente te muestran la gráfica y entre varias opciones es necesario saber a qué función logarítmica se corresponde.

    Muchísimas gracias!

    reply•thumb_up•0 voto/s•flag
    icon

    Hugo
    el 29/11/16

    Graficar una funcion donde aparezcan logaritmos es sencillo si entiendes la definicion de logaritmo [ log(x) = b <==> 10^b = x ] ,  para f(x) = log(x) lo que haces es calcular su dominio para saber a partir de que numeros se puede empezar a reemplazar en la variable ''equis''; haces que lo de dentro del logaritmo siempre sea positivo pero nunca cero, esto es x>0 ==> x∈ (0,+inf) ; reemplazar por ejemplo el 1 ; f(1) = log(1) = 0 [ devuelvete a la definicion, log(1) = 0 por que 10^0 = 1  y para x = 1 resulta ser imagen cero (1,0) ]

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Carlos Ojeda
    el 28/11/16

      Hola, pido ayuda a los profesores Antonio y César, no me sale esta integral, y no sé cuál es mi error. Gracias


    reply•thumb_up•0 voto/s•flag
    icon

    Hugo
    el 29/11/16

    Estas
    estas compitiendo y debes disfrutar, entrega total

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carlos Ojeda
    el 30/11/16

    Gracias


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Matias
    el 28/11/16

    Hola, queria saber si esta bien resuelta esta integral  

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 28/11/16

    Sin desarrollar la potencia Ezequiel:

    ∫ (5x+1)3dx ⇔ 1/5 ∫5(5x+1)3dx ⇔ 1/5 . (5x+1)4/ 4 ⇔ (5x+1)4/ 20 + C  

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Axel Morales Piñón.
    el 28/11/16

    Cómo se resolvería esta ecuación, me queda algo sin sentido):


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 29/11/16

    Antes que todo, observa que debe cumplirse: θ ≠ (2k+1)π/2, con k ∈ Z.

    Luego, podemos aplicar la identidad trigonométrica: 1 + tan2θ = sec2θ, sustituimos y queda:

    cosθ * √(sec2θ) = 1, elevamos al cuadrado en ambos miembros y queda:

    cos2θ * sec2θ = 1, asociamos exponentes y queda:

    (cosθ * secθ)2 = 1, aplicamos la identidad trigonométrica para la secante y queda:

    (cosθ * 1/cosθ) = 1, simplificamos y llegamos a:

    1 = 1, que es una identidad verdadera, por lo que concluimos que la ecuación tiene infinitas soluciones, y su conjunto solución queda:

    S = {θ ∈ R: θ ≠ (2k+1)π/2, con k ∈ Z}.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carla
    el 28/11/16

    Cómo calculo el valor de k para que se cumpla esta condición?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Podemos plantear para las raíces del polinomio cuadrático:

    x1 = a, x2 = 3a, luego pasamos a la expresión factorizada (observa que el coeficiente principal es igual a 4):

    P(x) = 4(x - x1)(x - x2), sustituimos las expresiones de las raíces:

    P(x) = 4(x - a)(x - 3a), distribuimos los agrupamientos y queda:

    P(x) = 4(x2 - 3ax - ax + 3a2), reducimos términos semejantes en el agrupamiento y queda:

    P(x) = 4(x2 - 4ax + 3a2),  distribuimos y queda:

    P(x) = 4x2 - 16ax + 12a2.

    Luego comparamos términos semejantes con la expresión del polinomio del enunciado y queda:

    4 = 4 (al comparar términos cuadráticos),

    - 16a = - 8 (al comparar términos lineales),

    12a2 = 2k + 1 (al comparar términos constantes);

    luego, de la segunda ecuación puedes despejar: a = 1/2, reemplazas en la tercera ecuación y queda:

    12(1/2)2 = 2k + 1, de donde despejas y llegas a: 1 = k.

    Luego, las raíces del polinomio son: x1 = 1/2, x2 = 3/2, y su expresión es: P(x) = 4x2 - 8k + 3.

    Espero haberte ayudado.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Carla
    el 29/11/16

    Me quedó casi todo claro, excepto el comienzo, por qué se pasa a la expresión factorizada?, con qué se trabaja ahí?

    "luego pasamos a la expresión factorizada (observa que el coeficiente principal es igual a 4):

    P(x) = 4(x - x1)(x - x2), sustituimos las expresiones de las raíces:"

    Asumo que eso corresponde al 4x2  , pero por qué se toma en cuenta sólo eso y no el -8x+2k+1?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonio Silvio Palmitano
    el 29/11/16

    Un polinomio de grado 2, de la forma:

    P(x) = ax2 + bx + c, puede ser factorizado como:

    P(x) = a(x - x1)(x - x2), donde x1 y x2 son las raíces del polinomio.

    Recuerda que para factorizar un polinomio, debemos tener en cuenta:

    - su coeficiente principal,

    - sus raíces: x1, x2,

    - los factores asociados a las raíces: (x - x1), (x - x2).

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Alexis de Barros
    el 28/11/16
    flagflag

    Hola, alguien podría ayudarme con este ejercicio 

    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 29/11/16

    Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

    Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
  • icon

    aida
    el 28/11/16

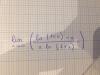    Hola buenas! Resulta que tengo un limite tal que este que te dejo en foto, nose muy bien que metodo tengo que usar ni como resolverlo. Ayudaaa!!!

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Observa que es indeterminado, ya que el numerador (N) y el denominador (D) tienden a cero. Luego, aplicaremos la Regla de L'Hôpital, y para ello preparamos las derivadas:

    N ' = 1/(1+x) - 1 = ( 1 - (1+x) )/(1+x) = -1/(1+x),

    D ' = ln(1+x) + x/(1+x) = ( (1+x)ln(1+x) + x )/(1+x).

    Luego, pasamos al cálculo del límite:

    Lím(x->0) N/D = aplicamos la Regla de L'Hôpital (obsrva que simplificamos denominadores):

    = Lím(x->0) (- 1) / ( (1+x)ln(1+x) + x ) = infinito (observa que el numerador es -1, y que el denominador tiende a 0).

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante