logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    ana
    el 28/11/16

    Tengo que resolver este sistema y= -3x2 + 6x+3               y=-x2 +4x-1  y yo lo resolvi haciendo     Y=Y  al final me queda en -0,8 pero hice algo mal y no se que es, y es muy importante sacar el resultado correcto porque despues tengo que que graficarla en un grafico.

    Gracias :)

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Comencemos por igualar, como indicas, y queda:

    - x2 + 4x - 1 = - 3x2 + 6x + 3, hacemos pasajes de términos y queda:

    - x2 + 4x - 1 + 3x2 - 6x - 3 = 0, reducimos términos semejantes y queda:

    2x2 - 2x - 4 = 0, dividimos por 2 todos los términos de la ecuación y queda:

    x2 - x - 2 = 0, observa que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y quedan sus soluciones:

    a) x = -1, reemplazamos en las ecuaciones iniciales, resolvemos y queda: y = - 6;

    b) x =2, reemplazamos en las ecuaciones iniciales, resolvemos y queda: y = 3.

    Luego, concluimos que el conjunto solución del sistema de ecuaciones queda:

    S = { (-1,-6) , (2,3) }.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    ana
    el 30/11/16

    porque haces aca el pasaje de termino todo de repente??? es lo mismo que si lo cambiamos de a poco???

     - x2 + 4x - 1 + 3x2 - 6x - 3 = 0

    Poruqe cuando no hago el pasaje de termino todo junto no recibo lo mismo que vos, y cuando lo hago pasando todo junto hay si me da tu resultado.

    Y al ultimo que dividis todo por 2 es para que te quede 2x2 como x2  ???

    Muchas gracias :)


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Gisel .A
    el 28/11/16

    No entiendo este ejercicio :tema induccion 

    2^n-5^n divisible por 7

    Gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Por favor, verifica que esté correcto el enunciado del ejercicio para que podamos ayudarte.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    LEO LACH
    el 28/11/16

    Una ayuda con este problema de distribución normal.


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 28/11/16


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    LEO LACH
    el 28/11/16

    Gracias :O

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    andres
    el 28/11/16

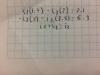    Muy buenas, me podrían ayudar con este sistema de ecuaciones, me confunde un poco lo de las multiplicaciones, tengo que obtener i1,i2,i3 

    gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Gabriel
    el 28/11/16

    Si te resulta más fácil, sustituye i1, i2 e i3, por x, y, z

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Vamos con la sugerencia del colega Gabriel, y denominamos: i1 = x, i2 = y, i3 = z. Luego, el sistema de ecuaciones queda:

    1,9x - 2z = 2,1

    - 2z - 3,5y = 6,3

    x + z = y,

    luego multiplicamos por 10 en la primera y en la segunda ecuación y queda:

    19x - 20z = 21, de donde despejamos: x = (21 + 20z)/19 (*),

    - 20z - 35y = 63, de donde despejamos: (- 20z - 63)/35 = y (**),

    x + z = y,

    luego sustituimos las expresiones señaladas (*) (**) en la tercera ecuación y queda:

    (21 + 20z)/19 + z = (- 20z - 63)/35, multiplicamos en todos los términos de la ecuación por 35 y por 19, simplificamos y queda: 

    35(21 + 20z) + 665z = 19(- 20z - 63), distribuimos agrupamientos y queda:

    735 + 700z + 665z = - 380z - 1197, hacemos pasajes de términos, reducimos términos semejantes y queda:

    1745z = - 1932, hacemos pasaje de factor como divisor, resolvemos y queda:

    z = - 1932/1745 ≅ - 1,107.

    Luego reemplazamos en la ecuación señalada (**), resolvemos y queda:

    y ≅ -1,167;

    luego reemplazamos en la ecuación señalada (*), resolvemos y queda:

    x ≅ - 0,060.

    Luego, concluimos que la solución del sistema es: i1 ≅ -0,060, i2 ≅ -1,167, i3 = - 1,107.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Antonella Correa
    el 28/11/16

    Hola! Necesito ayuda con un ejercicio de derivada, usando el criterio de la primera derivada, cómo lo resuelvo? 

    reply•thumb_up•0 voto/s•flag
    icon

    Gabriel
    el 28/11/16

    ¿Qué es lo que te piden exactamente? puedes enviarnos una imagen del enunciado?


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

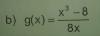
    Antonio Silvio Palmitano
    el 28/11/16

    Observa que el dominio de la función es: D = R - {0}, y que la expresión de la función puede escribirse:

    g(x) = (x3 - 8) / 8x = x3 / 8x - 8 / 8x, simplificamos y queda:

    g(x) = x2/8 - 1/x, luego planteamos la expresión de la función derivada:

    g ' (x) = x/4 + 1/x2, luego planteamos la condición de punto crítico::

    g ' (x) = 0, sustituimos y queda:

    x/4 + 1/x2 = 0, hacemos pasaje de término y queda:

    x/4 = - 1/x2, hacemos pasajes de divisores como factores y queda:

    x3 = - 4, hacemos pasaje de potencia como raíz y queda.

    x = ∛(-4) ≅ -1,587.

    Luego, el dominio nos queda subdividido en tres intervalos, elegimos un representante para cada uno, y evaluamos el signo de la derivada primera:

    ( -inf,∛(-4) ), representado por x = -2, y para él tenemos: g ' (-2) = - 1/4 < 0, por lo que la función es decreciente en este intervalo;

    ( ∛(-4) , 0), representado por x = -1, y para él tenemos: g ' (- 1) = 3/4 > 0, por lo que la función es creciente en este intervalo;

    ( 0 , + inf), representado por x = 1, y para él tenemos: g ' (1) = 5/4 > 0, por lo que la función es creciente en este intervalo;

    luego, observa que x = ∛(-4) es la abscisa de un mínimo de la función.

    Luego, queda para que completes el estudio de la función (cortes con los ejes, asíntotas y gráfico).

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonella Correa
    el 28/11/16

    Sii muchas gracias!! Una duda, cómo sacó la derivada de la función?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Ángel
    el 28/11/16

    g(x) =   x2/8   -   1/x                    


    g´(x)= (2x*8 - x2*0)/82   -     (-1/x2)

    g´(x)=            (2x*8)/82   -     (-1/x2)

    g´(x)=            (2x)/8   -     (-1/x2)

    g´(x)=            2x/8      +    1/x2

    g´(x)=            x/4      +    1/x2

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonella Correa
    el 28/11/16

    Muchas gracias!! 

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Gabriel
    el 28/11/16

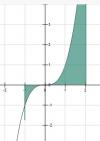
    Buenas noches. Como seria para plantear el area,mediante integrales, del siguiente enunciado:

    Me dan y=x^3                            y=0                con x=-1   x=2

    Lo que entiendo es que, esos dos valores de x serian como lo spuntos de corte, o los puntos desde donde se evaluara la integral. Pero el planteo de las integrales es la duda.Como seria la manera correcta de plantear el calculo del area?

    reply•thumb_up•0 voto/s•flag
    icon

    Gabriel
    el 28/11/16

    Hola tocayo :D

    Es calcular el área que barre esa curva entres -1≤x≤2. Sepáralo en dos integrales definidas, la primera -1≤x≤0 +  la segunda 0≤x≤2, y considera el valor absoluto de ambas, puesto que estás sumando áreas y al estar parte de la gráfica por debajo de y=0, te saldría negativo. Te adjunto una imagen para que lo puedas ver mejor.

    Espero haberme sabido expresar..


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Gabriel
    el 28/11/16

    Perfecta la explicacion amigo!.Gracias  

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Pedro
    el 28/11/16

    • Por favor ayúdenme a factorizar el siguiente polinomio 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Por favor, envía el enunciado del problema para que podamos ayudarte.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
  • icon

    Marco
    el 28/11/16

    Unicoos suUnicoos su ayuda por favor ayuda por favor

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 28/11/16

    Te va la segunda Marco.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Axel Morales Piñón.
    el 28/11/16

    Para la segunda, igualmente has el cambio de variable t = 2y3+ 3y2+6y ⇔ dt = (6y2 + 6y + 6)dy


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Axel Morales Piñón.
    el 28/11/16

     Te la dejamos para que la remates, evaluando los límites de integración correspondiente: 


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Axel Morales Piñón.
    el 28/11/16

    Pequeño lapsus, en el segundo comentario, me refería a hacer ese cambio de variable pero en la primera integral :p

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Carla
    el 28/11/16

    Hola, cómo puedo calcular el valor de eso en los números complejos?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Recuerda: i = eiπ/2, luego el valor principal de su logaritmo natural queda: Ln(i) = iπ/2.

    Luego tenemos:

    z = ii = (  eiπ/2 )i, multiplicamos los exponentes, resolvemos y queda:

    z = e-π/2.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Vicka
    el 28/11/16

    Hola tengo una duda sobre funciones homograficas:

    si quisiera pasar de f(x)= (ax+b)/(cx+d) a f(x)= k/(x-x0) + y0 (forma canonica) como hago?


    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 28/11/16

    Observa que puedes trabajar con el numerador (consideramos c ≠ 0):

    ax + b = multiplicamos y dividimos por c = a(cx)/c = sumamos y restamos d en el agrupamiento =

    = a(cx + d - d)/c = agrupamos dentro del agrupamiento = a( (cx + d) - d)/c = distribuimos = (a/c)(cx + d) - ad/c.

    Luego, sustituimos en la expresión de la función, distribuimos el divisor y queda:

    f(x) = (ax + b)/(cx + d) = ( (a/c)(cx + d) - ad/c )/(cx + d), distribuimos el divisor, simplificamos en el primer término y queda:

    f(x) = a/c - (ad/c)/(cx + d), ordenamos términos y llegamos a:

    f(x) = - (ad/c)/(cx + d) + a/c,

    observa que tenemos:

    k = - ad/c

    y0 = a/c.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?