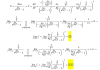-
fabian
el 27/11/16 -
andres
el 27/11/16Dada la función: f(X)= (-X+3)3*X
a) Calcular la ecuación de la recta tangente a la función ( FX) en el punto X=1 =b) Calcular el polinomio de Taylor de grado 2 de la función (FX ) en el punto X=1
Nota: Desarrollar la solución expresada en la forma AX2+BX +C).
c) Calcular la imagen de la función en el punto X=1,25 y la aproximación que de esta nos da la recta
tangente y el polinomio de Taylor de grado 2 calculados en los apartados anteriores. Comparar los
resultados indicando cuál de las aproximaciones es más precisa.
d) Dibujar con el GNUPLOT (en una misma gráfica) las gráficas de la función (FX ) , de la recta tangente y del polinomio de Taylor de grado 2 en el rango de lasx ∈ [ 1,6] Y∈ [ 10,10]
Antonio Silvio Palmitano
el 28/11/16Observa que puedes desarrollar y distribuir, y la expresión de la función (cuyo dominio es R) queda:
f(x) = - x4 + 9x3 - 27x2 + 27x
luego planteamos las expresiones de su derivada primera y de su derivada segunda:
f ' (x) = - 4x3 + 27x2 - 54x + 27
f ' ' (x) = - 12x2 + 54x - 54.
a) Evaluamos la función y a su derivada primera para x = 1 y queda:
f(1) = 8, f ' (1) = - 4;
luego, la expresión de la recta tangente a la gráfica queda:
y = - 4(x - 1) + 8.
b) Evaluamos la derivada segunda para x = 1 y queda:
f ' ' (1) = -12;
luego planteamos el Polinomio de Taylor con centro de desarrollo x0 = 1 y queda:
P(x) = 8 - 4(x - 1) - (12/2!)(x - 1)2 = 8 - 4(x - 1) - 6(x - 1)2, desarrollamos términos y queda:
P(x) = 8 - 4x + 4 - 6x2 + 12x - 6, reducimos términos semejantes, ordenamos y queda:
P(x) = - 6x2 + 8x + 6.
c) Evaluamos para x = 1,25:
- en la expresión de la función: f(1,25) = 6,69921877,
- en la expresión de la recta tangente: y = 7,
- en la expresión del Polinomio de Taylor: P(1,25) = 6,625;
con lo que tenemos que la aproximación que brinda el polinomio es más precisa que la que brinda la expresión de la recta tangente.
Queda para que hagas los gráficos con el programa informático.
Espero haberte ayudado.
-
Alba
el 27/11/16
Por favor, ¿alguien sabría hacer este ejercicio? No consigo obtener las soluciones. Gracias.
Alba
el 27/11/16
Antonius Benedictus
el 28/11/16Jesús Martínez Verdejo
el 28/11/16
Antonius Benedictus
el 28/11/16 -
Alba
el 27/11/16 -
Martina
el 27/11/16 -
fabian
el 27/11/16 -
Cristina
el 27/11/16¿Estaría bien el siguiente ejercicio de pasar de una función de densidad a una de distribución?
Antonio Silvio Palmitano
el 27/11/16Has resuelto bien la expresión de la función de densidad de probabilidad.
Luego, has planteado bien en tu dibujo, cuál es la región genérica de la que debes determinar la expresión de su área (la zona rayada), para encontrar la expresión de la función de distribución de probabilidad.
Luego, observa en tu dibujo que tienes un triángulo "grande" y uno "pequeño", y que la zona rayada es la diferencia entre ellos.
Luego pasamos a las dimensiones de cada triángulo:
Triángulo Grande:
base = 2, altura = 1, y su área queda: AT = 1.
Triángulo pequeño:
base = 1 - x, altura = f(x) = - 0,5x + 0,5 = 0,5(- x + 1), y su área queda: Ap = (1 - x)0,5(-x+1)/2 = 0,25(x2 - 2x + 1) = 0,25x2 - 0,5x + 0,25;
luego pasamos a la expresión del área de la región rayada, que corresponderá con a expresión de la función de distribución:
AT - Ap = 1 - (0,25x2 - 0,5x + 0,25) = - 0,25x2 + 0,5x + 0,75.
Luego, la expresión de la función de distribución de probabilidad queda:
F(x) =
0 si x < -1
- 0,25x2 + 0,5x + 0,75 si -1 ≤ x ≤ 1
1 si x > 1
Espero haberte ayudado.
-
antonella
el 27/11/16Hola Unicoos despues tiempo vuelvo a ingresar a este portal web ,y me impresiona cuantos cambios y mejoras han hecho ,gracias unicoos por existir me ayudaron mucho :) ,Pero me he topado con este problema de programacion lineal y no se como plantearlo ,si alguien tiene conocimiento de este tema por favor ayudeme ,se lo agradeceria mucho.
Ángel
el 27/11/16Vayamos por orden....observa que:
el punto de localización 4 abarca los sectores 1-5 (tenemos que coger este punto porque no hay ninguna camara más que tenga el sector 1 en su dominio de visión),
a continuación (con carácter obligatorio también) habrá que escoger el punto de localización 8 (ya que es el únicoo que cubre el sector 6),
de igual manera seguiríamos con el pto de localización 6 (sólo él cubre el sector 10),
el siguiente sería el punto 9 (abarca el sector 11),
después tendríamos que coger el punto 7 (pues abarca el sector 13 que no estaba incluido en el anterior)
y por último escogeríamos el punto 3 (date cuenta que abarca la unión los puntos 1 y 2, por lo tanto estos son innecesarios)
Obtendríamos como solución final un conjunto Punto de localización P= {P4 , P8 , P6 , P9 , P7 , P3} que abarca o cubre todo el conjunto de los sectores
y un conjunto de Punto de localización innecesaria I= {P1 , P2 , P5 , P10}, que son los elementos del conjunto Universal que no están en P, esto es, I=U-P
-
Bryam Maldonado
el 27/11/16
buenos dias me pudieran ayudar con este ejercico porfavor
David
el 29/11/16Lo siento pero el enunciado no tiene ningun sentido.. ¿un vector generado por cuatro vectores? ¿un vector del plano? Hay infinitos...
Es posible, eso sí, que corresponda a un tema muy concreto que estás dando en la universidad. En ese caso, lo siento no puedo ayudarte.
Unicoos por ahora se queda en bachiller. Espero lo entiendas.Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
