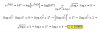Hola  Unicoos. Me piden hallar la ecuación de la recta tangente al gráfico f(x)= (5x+cos x)/(x+3) en el punto de abscisa x0= 0  . Gracias de antemano

Por favor ayudadme con este ejercicio lo mas pronto posible, tengo examen en unas horas, muchas gracias de antemano :D

Sea T: R³ -> R³ definida por T(vector x)= <vector x , vector y> * vector v = (vector x* vector v) * vector v , donde vector v*v=1, entonces T es una transformacion lineal. Construya una representacion geometrica que ilustre la forma en que transformas a cada vector x.

Necesito encontrar una ecuación del plano normal a la curva en P.

x=tsent

y=tcost

z=t

P(pi/2,0,pi/2)

Me pueden apoyar con la solución de la siguiente Ecuación Exponencial :

Buenas unicoos podrian ayudarme en este ejrtcicio. Me quedo estancado al sustituir los valores... ayudenmee!. 

Hola me piden demostrar que si una matriz admite al auto valor 0, entonces dicha matriz no es invertible o sea no tiene inversa.

Holas, por favor ayudadme con este ejercicio, mañana tengo examen :c, gracias :)

Determinar la dimension y una base para el espacio solucion del sistema:

x₁+ 2x₂ + 3x₃ = 0

x₁+ 3x₂ - x₃ = 0

2x₁ - 6x₂ + 8x₃ = 0

Buenas noches. Necesito un cable con esta integral.

∫tg^3(x).sec(x)dx  (integral de tangente al cubo por secante)

Como se hace para resolverla? Llegue a escribir la tg al cubo como el producto de tang^2 .tang..y despues a la tang^2 como sec^2 -1, pero me queda mas enrollado todavia.

A ver quien me saca de dudas:

Estoy haciendo este ejercicio en el cual tengo que extraer los vectores directores de la formulas anteriores i un punto. 

A continuación tengo que justificar si son paralelas, secantes o perpendiculares.

Pero con mis resultados no lo puedo verificar fácilmente, por ejemplo:

-Las rectas r i s son perpendiculares pero no puedo aplicar la siguiente formula (A,B) --> (-B,A) o (B,-A) únicamente se que son perpendiculares porque el producto de sus módulos (raíz de 40 i 50) multiplicados por el coseno de 90º es = 0. Pero supongo que esa explicación es muy rebuscada igual que la explicación que muestro en los apuntes de t i u:

Donde teóricamente  V1/U1 = V2/U2 

En mi caso el resultado es -2 i 2 afecto el cambio de signo?

-Una ultima pregunta si r i t són secantes como encuentro el punto de corte? Gracias!

Por favor resuelvan la 2 y la 1. Les agradeceria mucho muchoooo