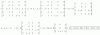Me da que falta una ecuacion asi que lo haría así 

Método de Gauss

El det =2 independientemente del valor de a

Aplicaremos la propiedad de los determinantes: "a una fila se le puede sumar o restar otra fila, y el valor del determinante no se altera".

Tenemos la matriz:

1      a         a²

1  (a+1)  (a+1)²

1  (a-1)   (a-1)²

A la fila 2 le restamos la fila 1, y a la fila 3 le restamos la fila 1:

1       a          a²

0       1       (2a+1)

0      -1      (-2a+1)

A la fila 3 le sumamos la fila 2:

1       a          a²

0       1       (2a+1)

0       0          2

Luego, como tenemos una matriz triangular (superior), tenemos que su determinante es igual al producto de los elementos de su diagonal principal, por lo que tenemos:

det(M) = 1*1*2 = 2 ≠ 0, para todo a ∈ R, por lo que el rango de la matriz es 3.

Espero haberte ayudado.

Llamemos r a la recta cuyas ecuaciones buscamos, y v = <a,b,c>, a su vector director.

Luego, el vector normal al plano es: n = <2,1,-1>, y como la recta es paralela al plano, tenemos que su vector director es perpendicular al vector normal del plano, por lo que planteamos:

n•v = 0.

Luego, el vector director de la recta que nos dan (que nos presentan como intersección de dos planos) será igual al producto vectorial de los vectores normales de los planos), por lo que planteamos:

u = n₁ x n₂ = <0,3,1> x <1,4,1> = <-1,1,-3>

y luego, como las dos rectas son perpendiculares, planteamos:

u•v = 0.

Luego, planteamos el sistema con las dos ecuaciones vectoriales remarcadas (expresamos las componentes de los vectores):

n•v = <2,1,-1> • <a,b,c> = 2a + b - c = 0 (*).

u•v = <-1,1,-3> • <a,b,c> = - a + b - 3c = 0 (**).
Luego, con las dos ecuaciones cartesianas señaladas tenemos el sistema:

 2a + b -   c = 0, hacemos pasaje de términos y queda: b = - 2a + c (***)

- a + b - 3c = 0

luego, sustituimos la ecuación señalada (***) en la segunda ecuación del sistema y queda:

- a - 2a + c - 3c = 0, reducimos términos semejantes y queda:

- 3a - 2c = 0, luego podemos despejar: c = -(3/2)a, sustituimos en la ecuación señalada (***) y queda:

b = - 2a - (3/2)a, resolvemos y queda: b = - (7/2)a,

luego, el vector director de la recta buscada queda:

v = <a,b,c> = <a,- (7/2)a,- (3/2)a> = a <1,-7/2,-3/2>, por lo que un vector director de la recta es:

V = <1,-7/2,-3/2>.

Luego, como tenemos un punto de la recta buscada ( A(1,2,-1) ), y su vector director V, podemos plantear sus ecuaciones cartesianas paramétricas:

x =  1 + 1t

y =  2 - (7/2)t

z = -1 - (3/2)t, con t ∈ R.

Espero haberte ayudado.

Observa que si los vectores u y v son paralelos (damos por sentado que no son nulos), puedes plantear: u = k v, con k ∈ R (*), y su módulo queda expresado: ||u|| = |k| ||v|| (**).

Luego, observa que los módulos de los vectores son números reales: ||u|| ∈ R, y ||v|| ∈ R, y ambos módulos son positivos y distintos de cero.

Luego, planteamos el producto escalar entre los vectores:

u/||u|| • v/||v|| = ordenamos factores y queda:

= ( 1 / ( ||u|| ||v|| ) u • v = sustituimos según las ecuaciones vectoriales señaladas (*) (**) y queda:

= ( 1 / ( |k| ||v|| ||v|| ) k v • v = resolvemos el producto escalar (observa que v • v = ||v||²) y queda:

= ( 1 / ( |k| ||v|| ||v|| ) k ||v||² = simplificamos y queda:

= k / ||k|| = ± 1, por lo que tenemos dos opciones: 

a) si k = 1 > 0, tenemos que los vectores son paralelos y de igual sentido,

b) si k = -1 < 0, tenemos que los vectores son paralelos y de sentidos contrarios.

Espero haberte ayudado.

No Alex, no tienen el mismo exponente.

De acuerdo con el colega Nelson. Lo que puedes hacer, a partir de la expresión:

sen²α - sen⁴α = extraemos factor común = sen²α(1 - sen²α) = aplicamos identidad trigonométrica = sen²α cos²α =

= (1/4) 4sen²α cos²α = asociamos factores cuadráticos = (1/4) (2senα cosα)² = aplicamos identidad trigonométrica = (1/4) sen²(2α).

Espero haberte ayudado.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Designemos a las cantidades de personas de cada nacionalidad, con la letra inicial de la misma (tenemos: p, t, g, a, i, que serán las cinco incógnitas a resolver).

Luego, a partir del enunciado, tenemos las ecuaciones:

p = a/3 - 1(la cantidad de polacos es igual al tercio de la cantidad de alemanes menos uno), multiplicamos por 3 y queda: 3p = a - 3

p = i/2 - 3 (la cantidad de polacos es igual a la mitad de la cantidad de italianos menos tres), multiplicamos por 2 y queda: 2p = i - 6

t + a = g + i + 3 (la cantidad de turcos y alemanes es igual a la cantidad de griegos e italianos mas tres), 

g + a = (a + p + t + g + i)/2 - 1 (la cantidad de griegos y alemanes es igual a la mitad del total menos uno), multiplicamos por 2 y queda: 2g + 2a = a + p + t + g + i - 2

i + g = 7(a + p + t + g + i)/16 (la cantidad de italianos y griegos es igual a siete dieciseisavos del total), multiplicamos por 16, distribuimos y queda:

16i + 16g = 7a + 7p + 7t + 7g + 7i

Luego hacemos pasajes de términos en todas las ecuaciones remarcadas, reducimos términos semejantes y queda el sistema:

a = 3p + 3 (*)

i = 2p + 6 (**)

a - g - i  + t = 3

a + g - i - p - t = -2

7a - 9g - 9i + 7p + 7t = 0

Luego sustituimos las expresiones de las ecuaciones remarcadas en las últimas tres ecuaciones, reducimos y queda:

- g + p + t = 6

 g - t = 1, despejamos y queda: g = t + 1 (***)

- 9g + 10p + 7t = 33

Luego sustituimos la expresión de la ecuación remarcada en las otras dos ecuaciones, reducimos y queda:

p = 7.

10o  - 2t = 42

Luego reemplazamos el valor de la ecuación remarcada en la segunda ecuación, reducimos y queda:

t = 14.

Luego reemplazamos en la ecuación señalada (***) y tenemos: g = 15.

Luego reemplazamos en la ecuación señalada (**) y tenemos: i = 20.

Luego reemplazamos en la ecuación señalada (*) y tenemos: a = 24.

Espero haberte ayudado.

Va armando , ve reduciendo por Gauss

Muy gentil, muchas gracias