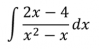Te van algunos apartados, intenta hacer lo restante (si no te sale mandas lo que está mal y te lo corrijo):

El dominio es el conjunto de elementos "x" que tienen imagen en f(x)

1. Observa que todas las x pueden tomar cualquier valor para dar un valor a f(x) excepto cuando el numerador se anule...ya que dará lugar a una indeterminación

2. Igualamos el denominador de f(x) a cero así: -2x+4=0 ---->   x=2

------->  Entonces teniendo en cuenta las dos premisas anteriores llegamos a la conclusión Dominio= D = (-inf,2) U (2,inf)

-------> La raíz de f(x) será cuando f(x)=0....entonces habrá que ver en qué valor se anula el numerador (y que ese mismo punto no coincida con x=2, para que la función no sea indeterminada)       3x+6=0----> x= -2 es la raíz

-------> La ordenada en el origen se refiere al valor de f(x) ó y cuando x=0 .....entonces sustituimos la x por cero en f(x):

        f(x)=  3x+6/-2x+4......f(0)=  (3*0+6)/(-2*0+4)= 6/4=3/2

*)Para el crecimiento/decrecimiento haz la primera derivada, calcula sus raíces, forma intervalos en la recta real con esas raíces y si te da mayor que cero en un intervalo será creciente y si es menor será decreciente

Para concavidad/convexidad haz la segunda derivada y si es mayor que cero será convexa y si es menor será cóncava (el procedimiento análogo a *)

Una serie alternada cuya sucesión base (en valor absoluto) es un infinitésimo monótono creciente es siempre convergente. En caso contrario, puede ser divergente.

Vamos con un contraejemplo.

Observa que la serie alternada con término general: an = (-1)ⁿ no es convergente (es oscilante). Por lo tanto, deben cumplirse las condiciones del Criterio de Leibniz para asegurar convergencia.

Espero haberte ayudado.

cual es la diferencia entre una serie convergente y otra oscilante? y que es un infinitesimo monotono?

=(

Debes expresar el argumento de la integral con fracciones parciales:

(2x-4) / (x²-x) = (2x-4) / x(x-1) = a/x + b/(x-1) = ( a(x-1) + bx ) / x(x-1),

luego comparamos numeradores, y evaluamos para dos valores arbitrarios de la variable x (observa que los más convenientes son 0 y 1)

a(x - 1) + bx = 2x - 4

para x=0 queda: -a = - 4, de donde despejamos: a = 4;

par x=1 queda: b = 2.

Luego, pasamos a la integral:
.I = ∫ ( (2x-4) / (x²-x) )dx = ∫ 4/x dx + ∫ 2/(x-1) dx = 4ln|x| + 2ln|x-1| + C.

Espero haberte ayudado.

Muchísimas gracias  Sr. Antonio

Por favor, verifica que el enunciado esté correcto y completo para que podamos ayudarte.

Halla las ecuaciones de las rectas tangentes comunes a la circunferencia  x²+y²+10x-20=0 y a la parábola y²=20x.

Vamos con una orientación.

Planteamos la ecuación de la recta tangente común en forma general, y luego planteamos las intersecciones entre ella y cada una de las curvas, que debe tener como solución única un punto de tangencia.

Planteamos la ecuación cartesiana explícita de la recta: y = mx + b.

Luego, planteamos su intersección con la parábola, mediante el sistema de ecuaciones:

y = mx + b

y² = 20x

sustituimos en la segunda ecuación y queda:

(mx + b)² = 20x, desarrollamos el primer miembro, hacemos pasaje de término y queda:

m²x² + 2mbx + b² - 20x = 0, agrupamos y factorizamos términos lineales y queda:

m²x² + 2(mb - 10)x + b² = 0, luego como debemos tener solución única, tenemos que el discriminante de la ecuación polinómica cuadrática debe ser igual a cero, y planteamos:

4(mb - 10)² - 4m²b² = 0, dividimos en todos los términos por 4 y queda:

(mb - 10)² - m²b² = 0 (*).

Luego planteamos la intersección de la recta con la circunferencia, mediante el sistema de ecuaciones:

y = mx + b

x2 + y2 + 10x -20 = 0

sustituimos en la segunda ecuación y queda:

x2 + (mx + b)2 + 10x -20 = 0, desarrollamos el binomio elevado al cuadrado y queda:

x2 + m²x² + 2mbx + b2 + 10x -20 = 0, agrupamos y factorizamos términos semejantes y queda:

(1 + m²)x² + 2(mb + 5)x + (b2 - 20) = 0, luego como debemos tener solución única, tenemos que el discriminante de la ecuación polinómica cuadrática debe ser igual a cero, y planteamos:

4(mb + 5)² - 4(1 + m²)(b2 - 20) = 0, dividimos en todos los términos por 4 y queda:

(mb + 5)² - (1 + m²)(b2 - 20) = 0 (**).

Luego, con las ecuaciones señaladas (*) (**) plantea un sistema, para encontrar la ecuación de la recta tangente común a la circunferencia y a la parábola (si haces un gráfico, verás que obtendrás dos rectas tangentes, cada una de ellas con un único punto de contacto con cada una de las curvas). El sistema queda:

(mb - 10)² - m²b² = 0

(mb + 5)² - (1 + m²)(b2 - 20) = 0

Luego, te dejo la resolución del sistema, y observa que puedes comenzar por desarrollar el binomio elevado al cuadrado en la primera ecuación.

Espero haberte ayudado.

Un punto frontera es aquél que cumple que, en cualquier entorno suyo hay puntos de A y de su complementario; pero puede ser que se trate solo de sí mismo. Esto es, un punto frontera es aislado o de acumulación, y puede o no pertenecer a A.

Hola, esto capaz te ayude bastante. Suerte

hola¡ muchísimas gracias. Pero no comprendo por que el menos dos al que esta elevado 27 luego pasa a elevar todo y  el xk  desaparece...siento mi ignorancia.

Genial!!!. Muchas gracias.
SIN EMBARGO, me resulto un poco complicado aplicar ese criterio..

Si me quede en ese desarrollo de taylor, como podria seguir en base al mismo para hallar esa derivada. 

En la fórmula de Taylor aparecen las derivadas sucesivas de la función, pero no es un método para calcularlas. Para la derivada n-ésima de un producto se utiliza la fórmula que te he puesto.

Ah genial Ahora si. Muchas gracias

Pon todas las rectas en forma general (o bien todas en forma explícita). Y usa esto:

¿Entonces esto es correcto?

Creo que sí.

No, Peter, no la has metido. lo que sucede es que esa ecuación no tiene solución real. El valor x=48 que has obtenido hace negativo algún argumento logarítmico y valdría como solución solamente si aceptamos logaritmos complejos.

De acuerdo con mi colega y tocayo, la ecuación no tiene solución real.

Observa también que x = 48 es solución, pero de la ecuación escrita en tu segunda línea, pero no lo es de la ecuación escrita en tu primera línea. La obtención de soluciones extrañas ocurre en este tipo de ecuaciones con frecuencia, por lo que se debe verificar su validez, como seguramente has hecho en este caso.

Espero haberte ayudado.