-
Me pueden ayudar por favor con la demostración de siguiente identidad trigonométrica: (1+sen x) / cos x + cos x / (1+sen x) = 2 secx


Antonio Silvio Palmitano
el 22/11/16Comencemos con el primer miembro de la igualdad (observa que es una expresión con dos términos fraccionarios):
(1+sen x) / cos x + cos x / (1+sen x) = extraemos denominador común y queda:
= ( (1+senx)2 + cos2x ) / cosx(1+senx) = desarrollamos el binomio elevado al cuadrado en el numerador:
= ( 1 + 2senx + sen2x + cos2x ) / cosx(1+senx) = aplicamos la identidad trigonométrica fundamental:
= ( 1 + 2senx + 1 ) / cosx(1+senx) = reducimos términos constantes en el numerador:
= ( 2 + 2senx) / cosx(1+senx) = extraemos factor común en el numerador:
= 2(1+senx) / cosx(1+senx) = simplificamos y queda:
= 2 / cosx = 2(1/cosx) = aplicamos la identidad de la secante:
= 2secx.
Espero haberte ayudado.
-
Hola tengo este ejercicio que creo haber resuelto bien (espero ya q tengo examen en unas horas y se basa en esto), a que se refiere con f(x)<0? que me pide hacer? Gracias!!!


Antonio Silvio Palmitano
el 22/11/16Tienes la expresión factorizada: f(x) = (x+6)(x-2)(x-4), luego pasamos a la inecuación:
f(x) < 0, sustituimos y queda:
(x+6)(x-2)(x-4) < 0, observa que el producto debe ser negativo (menor que cero), por lo que tenemos cuatro opciones:
a) x+6<0 y x-2<0 y x-4<0, despejas y queda: x<-6 y x<2 y x<4, que corresponde al intervalo: (-inf,-6);
b) x+6<0 y x-2>0 y x-4>0, despejas y queda: x<-6 y x>2 y x>4, que corresponde al intervalo: Φ (vacío);
c) x+6>0 y x-2<0 y x-4>0, despejas y queda: x>-6 y x<2 y x>4, que corresponde al intervalo: Φ (vacío);
d) x+6>0 y x-2>0 y x-4<0, despejas y queda: x>-6 y x>2 y x<4, que corresponde al intervalo: (2,4).
Luego, el conjunto solución de la inecuación, expresado como intervalo, queda: S = (-inf,-6) u (2,4).
Espero haberte ayudado.
-
ayuda mañana tengo exámenes y estoy colgado con las estadísticas en matemáticas
ATT: No entendi
-
Hola Unicoos,
¿Me ayudáis con la siguiente inecuación?
Gracias



Antonio Silvio Palmitano
el 22/11/16Asumiendo que el primer miembro es positivo, hacemos pasaje de raíz como potencia y queda:
3x2 + 6x + 2 ≤ (2x - 1)2 desarrollamos el segundo miembro y queda:
3x2 + 6x + 2 ≤ 4x2 - 4x + 1, hacemos pasajes de términos, reducimos términos semejantes y queda:
- x2 + 10x ≤ -1, multiplicamos en todos los términos de la inecuación por -1 (observa que cambia el sentido de la desigualdad) y queda:
x2 - 10x ≥ 1, sumamos 25 en ambos miembros (buscamos completar un trinomio cuadrado perfecto en el primer miembro) y queda:
x2 - 10x + 25 ≥ 1 + 25,, factorizamos el primer miembro, resolvemos el segundo miembro y queda:
(x - 5)2 ≥ 26, hacemos pasaje de potencia con exponente par como raíz (observa que queda valor absoluto en el primer miembro):
|x - 5| ≥ √(26), luego tenemos dos opciones:
a) x - 5 ≤ - √(26), que nos conduce a: x ≤ 5 - √(26), que corresponde al intervalo ( -inf , 5 - √(26) ); o:
b) x - 5 ≥ √(26), que nos conduce a: x ≥ 5 + √(26), que corresponde al intervalo ( 5 + √(26) , +inf ).
Por todo, concluimos que el conjunto solución expresado como intervalo queda: S = ( -inf , 5 - √(26) ) u ( 5 + √(26) , +inf ).
Espero haberte ayudado.
-
Hola buena noche, si tengo f (x) = x^2 I= [2,4] hallar su maximo y minimo, hice el procedimiento que según su maximo es 16 y 4 el minimo aunque dudo mucho que este bien, si alguien me pudiera rectificar por favor y resolver otras dudas que tengo:
-que pasa cuando I= a intervalos abiertos, habría un minimo y maximo en 'x' funcion?
-es posible hallar máximo y minimo en un intervalo abierto y el otro cerrado?
Muchas gracias aplico mañana y quiero que me aclaren estas dudas por favor, bendiciones.


Antonio Silvio Palmitano
el 22/11/16Recuerda el enunciado del Teorema correspondiente:
Si f es una función continua en un intervalo cerrado D, entonces f alcanza máximo absoluto y mínimo absoluto en D.
En el primer caso has resuelto bien: la función es continua, el intervalo es cerrado, y como la función es estrictamente creciente en el intervalo, tenemos que no presenta puntos críticos en él, por lo que tenemos un mínimo absoluto en el extremo izquierdo, y un máximo absoluto en el extremo derecho del intervalo.
Si el intervalo es abierto en los dos extremos, o semiabierto (con un extremos abierto y otro cerrado), no es posible aplicar el Teorema, y debemos realizar un estudio completo a fin de localizar máximos y mínimos absolutos.
Espero haberte ayudado.
-
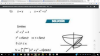
Hallar el volumen del solido limitado por las superficies :
No entiendo porque le hace esa parte de x^2+y^2=4
ayuda


David
el 22/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Alguien me podria verificar esto:
plano1: 3x-6y+3z=2
plano2: x-2y+2=7
tengo que verificar si son paralelos o perpendiculares. Yo lo hize, y me sale...3/1=-6=-2=3/0 no entiendo ahi como seria el 3/0..queda igual a 3?
Y el producto vectorial de los normales es distinto de 0 asi que perpendiculares no son.


Antonio Silvio Palmitano
el 22/11/16Tienes el vector normal al primer plano: u = <3,-6,3>, y el vector normal al segundo plano: v = <1,-2,0>.
Luego planteamos (llamamos N al vector nulo):
a) Condición de paralelismo entre planos (los vectores normales son paralelos): u x v = N (el producto vectorial entre los vectores normales tiene resultado nulo).
b) Condición e perpendicularidad entre planos (los vectores normales son perpenidculares): u • v = 0 (el producto escalar entre los vectores normales es igual a cero).
Observa que los planos son secantes, ya que puedes verificar que no son paralelos ni perpendiculares.
Espero haberte ayudado.
-


David
el 22/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Los molesto con dos consultas.
Para calcular el angulo entredos planos, seria cos= al producto escalar de los normales sobre el producto del modulo de los normales, o seria cos=al modulo del escalar de los normales sobre el producto del modulo de los normales?
Otra duda tonta, cuando calcule el angulo..la calculadora debe estar en radianes? o da igual?