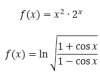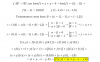-
Lorena Llanos
el 16/11/16Hola,
Por favor su ayuda con estas derivadas
Gracias
Ángel
el 16/11/16Ten cuenta que para el primero hemos usado:
*Si f(x)=u*v, entonces f´(x)= u´*v+u*v´
*Si f(x)=ln(u), entonces f´(x)= u´/u
y para el segundo:
*√x=(x)1/2
* Ln (x/y)= Lnx-Lny
*Si f(x)=ln(u), entonces f´(x)= u´/u
*la igualdad notable a2-b2= (a+b)(a-b),
*la relación trigonométrica sen2x + cos2x = 1
*la inversa del seno: 1/senx=cosecx
-
Adrian
el 16/11/16
Buenas tardes, mi profesor me ha dado la definición de diferenciales pero se me mezcló un poco, eso es 1 definición o dos?
-
Machacador1996
el 16/11/16Bueno lo mío, en realidad, no es una pregunta. Solo quería saber si unicoos va a subir algún vídeo de series de funciones para la universidad (asignatura de calculo) . si lo tiene subido agradecería que añadierais el link a la respuesta. Gracias.
-
María José Ledesma
el 16/11/16Hola! Como se calcula el área entre las siguientes funciones?
Dadas las funciones f (x) = 5x^3-x^2-4x , g(x)= x^2+ 3x
Gracias y saludos!!
Antonio Silvio Palmitano
el 16/11/16Primero buscamos los puntos de intersección entre las gráficas de las funciones, y para ello planteamos:
f(x) = g(x), luego sustituimos las expresiones de las funciones y queda:
5x3 - x2 - 4x = x2 + 3x, hacemos pasajes de términos, reducimos términos semejantes y queda:
5x3 - 2x2 - 7x = 0, extraemos factor común:
x(5x2 - 2x - 7) = 0, luego, por anulación de un producto tenemos:
a) x1 = 0;
b) 5x2 - 2x - 7 = 0, que es una ecuación polinómica cuadrática cuyas raíces son: x2 = -1 y x3 = 7/5.
Luego, tenemos dos intervalos, elegimos un representante en cada uno de ellos y evaluamos las expresiones de las funciones:
I1 = (-1,0), representado por x = -1/2, y para él tenemos: f(-1/2) = 9/8, g(-1/2) = -5/4, por lo que en este intervalo tenemos: f(x) > g(x);
I2 = (0,7/5), representado por x = 1, y para él tenemos: f(1) = 0, g(1) = 4, por lo que en este intervalo tenemos: g(x) > f(x).
Luego, plantearemos el área de la región limitada por las gráficas de las funciones como suma de dos integrales, una para cada intervalo:
A = A1 + A2
Luego, tenemos:
A1 = ∫ ( f(x) - g(x) )dx = ∫ (5x3 - x2 - 4x - x2 - 3x)dx = ∫ (5x3 - 2x2 - 7x)dx = queda para que continúes la tarea;
A2 = ∫ ( g(x) - f(x) )dx = ∫ (x2 + 3x - 5x3 + x2 + 4x)dx = ∫ (- 5x3 + 2x2 + 7x)dx = queda para que continúes la tarea.
Espero haberte ayudado.
-
Alejandro Colocho
el 16/11/16Hola me surgió una duda con un ejercicio y quiero saber si la funcion f(x)= x - 1/x es continua?
Ángel
el 16/11/16
Machacador1996
el 16/11/16la funcion f(x)=(x-1)/x no es continua. solo es continua en el intervalo (menos infinito, 0 ) unión ( 0, + infinito) ; es decir la función es continua en todo R menos 0. Cuando x vale 0, el denominador es 0, y por lo tanto como no se puede dividir entre 0 porque es imposible, la función no existe en x=0.
-
Flor
el 15/11/16Hola buenas tardes quería hacer una pregunta del tema transformaciones lineales.
Dice: definir, si es posible, una transformación lineal tal que:
1) F: R^2-->R^3. N(f) = {(X1, X2)/ X1 = X2}
2) f: R^2-->R^3. F(-1,2)=(1,-1,0). N(f)={(X1, X2)/X1+X2=0}
En el primero busque una base como (1,1) para que cumpliera con la condición del núcleo y luego lo iguale a (0,0,0), después tome generadores linealmente independientes y calcule la imagen dándole cualquier valor pero de R^3. Pero no se si hago bien y tampoco se como seguirlo. Les agradezco.. el segundo no pude empezar. Saludos!
-
andres
el 15/11/16 -
Laura
el 15/11/16Buenas yo tengo dudas con los problemas de programación lineal, tengo que buscar la función objetivo y las restricciones eso más o menos lo sé hacer, pero luego cuando ya está representada gráficamente y busco el punto (0,0) tengo que buscar en los vértices cuantos puntos hay y calcularlos y no sé como se calculan, adjunto foto con ejemplo de problemas,
David
el 16/11/16No puedo haceros los deberes de 4 en 4, y menos de programacion lineal que son larguisimos y hacer que hacer dibujos, etc.
Lo que si puedo decirte es que tienes varios vídeos de esa lección que estoy casi convencido de que solucionarán todas tus dudas... echales un vistazo.
Programación lineal
A partir de ahí, si tienes dudas concretas sobre algun ejercicio concreto envianos una foto con todo lo que consigas y te echamos un cable. Besos! -
cinthia
el 15/11/16ayuda para poder plantear este problema, es de una DISTRIBUCION MULTINOMIAL: Hallar la probabilidad de no obtener un 1, 2 ó 3 en cuatro lanzamiento de un dado honrado(que no es un dado arreglado) desde ya muchas gracias.... 😀
Ángel
el 15/11/16
