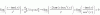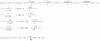-
S. UNSIRIO
el 15/11/16Hola estoy preparando un examen y tengo muchas dudas. Me hubiera gustado mucho haberlos encontrado unos meses atras para preparar mejor mi examen, ahora ya no tengo mas q una semana :( Probe con otros lugares online y no me resultaron. Quisiera ademas de felicitarlos agradecerles por el excelente trabajo que realizan!
Tengo dos tipos de ejercicios que resolver. De uno trabaje lo que pude pero no se como seguir el ejercicio, no se como despejar "a". A continuacion les dejo lo que pude hacer del ejercicio 4, yo creo que hice tod mal.. :(
2x^3-12x^2+16x-2ax^2+12ax-16a
(2x^3-12x^2+16x)(-2ax^2+12ax-16a)
2x(x^-6x+8)-2a(x^2-6x+8)
(x^2-6x+8)(2x-2a)
Antonio Silvio Palmitano
el 15/11/16Vamos con el ejercicio 4.
Tienes dos raíces (o ceros) conocidos:
β = 2, cuyo factor elemental es: (x-2);
γ = 4, cuyo factor elemental es (x-4);
α es una raíz que debemos determinar, cuyo factor elemental es: (x-α):
también tenemos el coeficiente principal: A = 2;
y también tenemos: f(0) = 48.
Luego, planteamos la expresión de la función:
f(x) = A(x-α)(x-β)(x-γ), reemplazamos las raíces conocidas y el coeficiente principal y queda:
f(x) = 2(x-α)(x-2)(x-4) (*), luego evaluamos para x = 0 y queda:
f(0) = 2(0-α)(0-2)(0-4) = 48, resolvemos factores y queda:
2(-α)(-2)(-4) = 48, resolvemos en el primer miembro queda:
- 16α = 48, hacemos pasaje de factor como divisor, resolvemos el segundo miembro y queda:
α = - 3.
Luego, reemplazamos en la expresión señalada (*) y llegamos a:
f(x) = 2(x + 3)(x - 2)(x - 4).
Positividad: planteamos f(x) > 0. Observa que tenemos cuatro opciones:
a) x+3>0 y x-2>0 y x-4>0, que corresponde al intervalo (4,+inf);
b) x+3>0 y x-2<0 y x-4<0, que corresponde al intervalo (-3,2);
c) x+3<0 y x-2>0 y x-4<0, que corresponde al intervalo vacío;
d) x+3<0 y x-2<0 y x-4>0, que corresponde al intervalo vacío;
por lo que concluimos que el conjunto de positividad es: Ip = (-3,2) u (4,+inf).
Negatividad: planteamos f(x) < 0.. Observa que tenemos cuatro opciones:
a) x+3<0 y x-2<0 y x-4<0, que corresponde al intervalo (-inf,-3);
b) x+3>0 y x-2>0 y x-4<0, que corresponde al intervalo (2,4);
c) x+3<0 y x-2>0 y x-4>0, que corresponde al intervalo vacío;
d) x+3>0 y x-2<0 y x-4>0, que corresponde al intervalo vacío;
por lo que concluimos que el conjunto de negatividad es: In = (-inf,-3) u (2,4).
Observa que los intervalos se corresponden con la gráfica del enunciado.
Luego, para plantear el conjunto solución para la inecuación: f(x) ≥ 0, consideramos el conjunto de positividad, y le agregamos las raíces que tengamos en los extremos del intervalo.
Por lo tanto, el conjunto solución para esta inecuación queda: S = Ip u {-3,2,4} = [-3,2] u [4,+inf).
Espero haberte ayudado.
-
Ángel
el 15/11/16Me piden calcular:
A) El máximo y el mínimo en
[-1,1] de f(x)= ∛x +
|x|
B)¿Podemos asegurar que los
extremos se alcanzan en puntos de ese intervalo? ¿Porqué?SU MÍNIMO SÍ (-√1/27,
-√3/3), PERO SU MÁXIMO NO¿Porqué?
PORQUE LOS LIMITES
LATERALES DE LA DERIVADA TIENDEN A INFINITO...¿está bien resuelto y
respondido?
Gracias
Antonius Benedictus
el 16/11/16La función es continua por doquier (aunque no sea derivable en x = 0). El teorema de Weierstrass asegura la existencia de extremos absolutos en cualquier intervalo cerrado. Y el Teorema de Fermat te va a decir que los busques en los extremos del intervalo y en los puntos críticos (de derivada 0 o sin derivada).
-
Jose
el 15/11/16Hola unicoos el ejercicio me dice
a) Hallar la formula de la transformacion lineal F : R2--> R2 / Nu(F) = {(x;y;z)∈ R3/ x-y+2z=0} Im(F)= gen{(1;-1)}. Es dicha TL unica?
b) Hallar la formula de la transformacion lineal T: R2--> R2 si Nu(F)= gen{(-1;1)} y λ=2 es un autovalor asociado a T y al autovector v(0;1). Es unica?
Ayudenme por favor
-
inmaculada
el 15/11/16 -
Ania
el 15/11/16
Hola me gustaría saber como puedo sacar la base de U+V, teniendo en cuenta las condiciones estipuladas cada conjunto de vectores.
U= {(x1, x2, x3, x4) / x1+x2-x3=0; x1-x4=0}
V={(x1, x2, x3, x4) / x1-x3-x4=0; x1-x4=0}
Gracias
David
el 16/11/16Echales un vistazo a estos vídeos... Subespacios vectoriales
A partir de ahí, me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendasOjalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Javier García
el 15/11/16 -
Loqpe
el 15/11/16Necesito discutir este sistema
- ax + y + z = a
- x + ay + z = a
- x + y + az = a
Que seria
- a + 1 + 1 = a
- 1 + a + 1 = a
- 1 + 1 + a = a
Si "a" vale 1 seria S.C.I o S.I? Y si vale 0?
Gracias!
Antonio Silvio Palmitano
el 15/11/16Tienes tres casos: a) a = 0, b) a = 1, y c) a ≠ 0 y a ≠ 1.
1) Reemplazamos y queda la matriz ampliada:
0 1 1 0
1 0 1 0
1 1 0 0
Permutamos la fila 1 con la fila 2 y queda:
1 0 1 0
0 1 1 0
1 1 0 0
A la fila 3 le restamos la fila 1 y queda:
1 0 1 0
0 1 1 0
0 1 -1 0
A la fila 3 le restamos la fila 2 y queda:
1 0 1 0
0 1 1 0
0 0 -2 0
Multiplicamos a la fila 3 por 1/2 y queda:
1 0 1 0
0 1 1 0
0 0 1 0
A la fila 1 le restamos la fila 3, a la fila 2 le restamos la fila 3 y queda:
1 0 0 0
0 1 0 0
0 0 1 0
Luego, concluimos que el sistema es compatible determinado, y que la solución es: x = 0, y = 0, z = 0.
b) Reemplazamos y queda:
1 1 1 1
1 1 1 1
1 1 1 1
A la fila 2 le restamos la fila 1, a la fila 3 le restamos la fila 1 y queda:
1 1 1 1
0 0 0 0
0 0 0 0
Luego, observa que el sistema de ecuaciones equivalente queda:
x + y + z = 1, de donde podemos despejar: z = - x - y + 1.
0 = 0, que es una identidad verdadera,
0 = 0, que es una identidad verdadera.
Luego, concluimos que el sistema es compatible indeterminado, y sus soluciones quedan expresadas: x ∈ R, y ∈ R, z = - x - y + 1.
c) Tenemos la matriz ampliada:
a 1 1 a
1 a 1 a
1 1 a a
Permutamos la filia 3 con la fila 1 y queda:
1 1 a a
1 a 1 a
a 1 1 a
A la fila 2 le restamos la fila 1, a la fila 3 le restamos la fila 1 multiplicada por a, y queda:
1 1 a a
0 (a-1) (1-a) 0
0 (1-a) (1-a2) (a-a2)
Dividimos a la fila 2 y a la fila 3 por (a-1) (que es distinto de cero), y queda:
1 1 a a
0 1 -1 0
0 -1 (-1-a) -a
A la fila 1 le restamos la fila 2, a la fila 3 le sumamos la fila 2, y queda:
1 0 (a+1) a
0 1 -1 0
0 0 (-2-a) -a
Luego, tenemos dos casos: c1) a = -2, y c2) a ≠ -2:
c1) Reemplazamos y queda:
1 0 -1 -2
0 1 -1 0
0 0 0 2
Luego, queda el sistema equivalente:
x - z = -2
y - z = 0
0 = 2, que es una identidad absurda, por lo que concluimos que el sistema es incompatible y no tiene solución.
c2) Dividimos a la fila 3 por -(a+2), que es distinto de cero, y queda:
1 0 (a+1) a
0 1 -1 0
0 0 1 a/(a+2)
A la fila 1 le restamos la fila 3 multiplicada por (a+1), a la fila 2 le sumamos la fila 3, y queda:
1 0 0 a - a(a+1)/(a+2)
0 1 0 a/(a+2)
0 0 1 a/(a+2)
Luego, concluimos que el sistema es compatible determinado, y su solución queda expresada:
x = a - a(a+1)/(a+2) = a/(a+2), y = a/(a+2), z = a/(a+2).
Espero haberte ayudado.
-
Matias Reyes
el 15/11/16Mi duda es este problema
Hallar z:
2z+iz/i80+i63=-1+2i
Se hacer la parte de los complejos pero no entiendo como resolver la parte de las z
-
Jose Manuel
el 15/11/16
Ayuda por favor examen mañana y es imposible
César
el 15/11/16 -
Albus99
el 15/11/16Buenas tardes, necesito ayuda con este ejercicio, estoy intentando plantearlo y no lelgo a conseguirlo:
Considere la recta r y el plano π dados por las ecuaciones r: x= y+2/-1=z-1/2 y π=2x+y+z=-7
Determine el plano α que pasa por el punto P(2,-3,3), es paralelo a r y perpendicular a π.
Vale, yo he sacado el vector director de r que en teoria es (1,-1,2). Después como α⊥π y α||r, entonces fácilmente se deduce que π⊥r ¿verdad? Entonces el vector normal de π tendría q ser el mismo que el de r como vectores libres no?? Pero (1,-1,2) ≠ (2,1,1), falla algo en el enunciado o me he equivocado yo en algo?? Gracias
