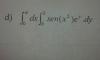-
Hola,
tengo la función f(x)=
x3+2x+2 si x<0
x2-3x+2 si x≥0
tengo que hallar:a) Continuidad y derivabilidad de f(x)
¿está bien hecho?
Gracias


Antonio Silvio Palmitano
el 15/11/16Vas bien encaminado, pero para formalizar correctamente la continuidad en x = 0 (punto de corte entre trozos) tenemos:
1) f(0) = 2 (observa que 0 pertenece al intervalo del dominio que corresponde al segundo trozo.
2) Límites laterales:
Lím(x-->0-) f(x) = Lím(x-->0-) (x3 + 2x +2) = 2
Lím(x-->0+) f(x) = Lím(x-->0+) (x2 - 3x + 2) = 2
luego, como los límites laterales coinciden, tenemos:
Lím(x-->0) f(x) = 2.
3) Como tenemos que f(0) = Lím(x-->0) f(x) = 2, concluimos que f(x) e continua en x = 2.
Luego, has señalado correctamente que la función es continua en R, y también que es derivable en R - {0}.
Espero haberte ayudado.
-
Tengo la función f(x)=
x3+2x+2 si x<0
x2-3x+2 si x≥0
tengo que hallar:b) Los extremos de f(x) en [-2,2]
¿está bien hecho?


Antonio Silvio Palmitano
el 15/11/16Has seleccionado bien los puntos notables, y justificado bien con el Teorema.
Observa en tu tabla de valores, que debes evaluar los puntos notables en la expresión de la función:
f(-2) = - 8 - 4 + 2 = -10 (lo hemos evaluado en la expresión del primer trozo),
f(0) = 0 - 0 + 2 = 2 (lo hemos evaluado en la expresión del segundo trozo),
f(3/2) = 9/4 - 9/2 + 2 = -1/4 (lo hemos evaluado en el segundo trozo),
f(2) = 4 - 6 + 2 = 0 (lo hemos evaluado en el segundo trozo).
Por lo tanto, concluimos que la función alcanza su valor míniimo absoluto en x = -2, y su valor mínimo absoluto en x = 0.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 15/11/16Vamos con orientaciones para los dos primeros problemas.
2) Tenemos para las coordenadas del centroide (es muy conveniente que grafiques la región):
xc = ∫ x(4-x2)dx / ∫ (4-x2)dx, con intervalo de integración: 0 ≤ x ≤ 2.
Luego, planteamos la ecuación explícita para x, queda: x = √(4-y), luego:
yc = ∫ y√(4-y)dy / ∫ √(4-y)dy, con intervalo de integración: 0 ≤ y ≤ 4.
3) Observa que las gráficas se cortan para x = 0 y x = 3, por lo que el intervalo de integración queda: 0 ≤ x ≤ 3, y observa que g(x) ≥ f(x) en el intervalo.
Luego planteamos:
G(x) = g(x) - (-1) = 4 - x + 1 = 5 - x,
F(x) = f(x) - (-1) = x2 - 4x + 4 + 1 = x2 - 4x + 5.
Luego planteamos el volumen de revolución alrededor del eje paralelo al eje OX, cuya ecuación es y = -1:
V = π ∫ ( G(x)2 - F(x)2 )dx, con intervalo de integración: 0 ≤ x ≤ 3 (te dejo la tarea para que la continúes).
Espero haberte ayudado.
-
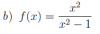
- Me podrian ayudar!
Me piden sacar todo esto de la funcion, y lo hice pero necesito corroborar si esta bien. - Dominio e Imagen
- Ceros
- Paridad
- Crecimiento - Decrecimiento
- Puntos criticos
- Extremos
- Convexidad y Concavidad
- Puntos de infleccion
- Asintotas.
- Hay algunas que no me dan por eso siento que esta mal si me podrian ayudar, les agradeceria.


Antonio Silvio Palmitano
el 15/11/16Tienes la función cuya expresión puede escribirse:
f(x) = x2/(x2 - 1) = ( (x2 - 1) + 1 ) / (x2 - 1) = (x2 - 1)/(x2 - 1) + 1/(x2 - 1) = 1 + 1/(x2 - 1) = 1 + (x2 - 1)-1.
Luego, pasamos a la expresión de su derivada primera:
f ' (x) = - 2x(x2 - 1)-2 = - 2x/(x2 - 1)2.
Luego, pasamos a la expresión de su derivada segunda:
f ' ' (x) = -2(x2 - 1)-2 + 8x2(x2 - 1)-3 = (x2 - 1)-3 ( -2(x2 - 1) + 8x2 ) = (x2 - 1)-3 ( 6x2 + 2 ) = ( 6x2 + 2 )/(x2 - 1)3 .
1) Dominio. A partir de la expresión de la función, observa que el denominador se anula para - 1 y 1, tenemos que el dominio es: D = R - { -1 , 1 }.
2) Imagen. A partir de la expresión de la función:
y = 1 + 1/(x2 - 1), hacemos pasaje de término y queda:
y - 1 = 1/(x2 - 1), hacemos pasaje de divisor como factor y queda:
(x2 - 1)(y - 1) = 1, hacemos pasaje de factor como divisor y queda (observa que y debe ser distinto de 1):
x2 - 1 = 1/(y - 1), hacemos pasaje de término y queda:
x2 = 1/(y - 1) + 1, extraemos denominador común, resolvemos a la derecha y queda:
x2 = y/(y - 1), observa que el primer miembro es positivo, por lo que el segundo debe ser positivo, y tenemos dos opciones:
a) y > 0 e y > 1, que conduce al intervalo (1,+inf);
b) y < 0 e y < 1, que conduce al intervalo (-inf,0).
Por lo tanto, concluimos que la imagen de la función es el conjunto: I = (-inf,0) u (1,+inf).
3) Ceros. Planteamos la ecuación:
f(x) = 0, sustituimos y queda:
1 + 1/(x2 - 1) = 0, hacemos pasaje de término y queda:
1 = -1/(x2 - 1), hacemos pasaje de divisor como factor y queda:
x2 - 1 = - 1, hacemos pasaje de término, resolvemos a la derecha y queda:
x2 = 0, que nos conduce a: x = 0.
4) Paridad. Planteamos la expresión:
f(-x) = 1 + 1/( (-x)2 - 1) = 1 + 1/(x2 - 1) = f(x), por lo que concluimos que la función es par.
5) Puntos críticos. Planteamos la ecuación:
f ' (x) = 0, sustituimos y queda:
- 2x/(x2 - 1)2 = 0, hacemos pasaje de divisor como factor, de factor como divisor, resolvemos a la derecha y queda:
x = 0.
6) Posibles puntos de inflexión. Planteamos la ecuación:
f ' ' (x) = 0, sustituimos y queda:
( 6x2 + 2 )/(x2 - 1)3 = 0, hacemos pasaje de divisor como factor, resolvemos a la derecha y queda:
6x2 + 2 = 0, hacemos pasaje de término y queda:
6x2 = -2, observa que es una igualdad absurda, ya que el primer miembro es positivo, y el segundo es estrictamente negativo,
por lo que concluimos que la gráfica de la función no presenta puntos de inflexión.
7) Asíntotas (te dejo la tarea de hacer los cálculos). Planteamos:
a) Asíntotas Horizontales: planteamos los límites de f(x) para x tendiendo a -infinito y tendiendo a +infinito.
b) Asíntotas Verticales: planteamos los límites por izuierda y por derecha en cada una de las discontinuidades: -1 y 1.
c) Asíntotas Oblicuas: planteamos los límites de la expresión f(x)/x para x tendiendo a infinito para la pendiente y, si existe y no es igual a cero, planteamos también el límite para x tiendiendo a infinito de la expresión (f(x) - mx).
8) Subdividimos el dominio en intervalos, con cortes en las discontinuidades, los puntos críticos y los posibles puntos de inflexión, planteamos un representante en cada intervalo, y evaluamos para ellos los signos de las expresiones de la derivada primera y de la derivada segunda. Tenemos los intervalos:
(-inf,-1), representado por x = -2, y para él tenemos: f ' (-2) > 0 y f ' ' (-2) > 0, por lo que tenemos que la gráfica es creciente y cóncava hacia arriba en este intervalo;
(-1,0), representado por x = -1/2, y para él tenemos: f ' (-1/2) > 0 y f ' ' (-1/2) < 0, por lo que tenemos que la gráfica es creciente y cóncava hacia abajo en este intervalo (*);
(0,1), representado por x = 1/2, y para él tenemos; f ' (1/2) < 0 y f ' ' (1/2) < 0, por lo que tenemos que la gráfica es decreciente y cóncava hacia abajo en este intervalo (*);
(1,+inf), representao por x = 2, y para él tenemos: f ' (2) < 0 y f ' ' (2) > 0, por lo que tenemos que la gráfica es decreciente y cóncava hacia arriba en este intervalo;
y a partir de las consideraciones señaladas (*) tenemos que la gráfica de la función presenta un máximo en x = 0, que luego con el gráfico se puede determinar que es un máximo local.
Queda para que completes la tarea.
Espero haberte ayudado.
-
Buenas tardes, me podrian dar la idea de como hacer el problema 2 y 3, lo que no entiendo es como puedo sacar la proyeccion de un vector en un plano, y como podria probar si una curva pertenece a un plano que me da como dato. Ayuda porfavor.


David
el 16/11/16No te piden la proyeccion de un vector sino la proyeccion de uns segmento..
Para ello, halla la proyeccion del punto A sobre el plano y luego la proyeccion del punto B sobre el plano...
Te vendrá genial este vídeo.. Punto simétrico a una recta en R³
Cuando hallo M, estoy hallando la proyeccion de un punto sobre un plano..
Nos cuentas ¿ok?
P.D. Con la torsión, lo siento, no puedo ayudarte. Se da en la universidad. Y solo en algunas carreras.. Por si te ayuda... http://matematicas.unex.es/~brequejo/GEOMETRIA_DIFERENCIAL_I/Capitulo%20II.pdf -
Hola Unicoos,
Me piden hallar las restantes razones trigonométricas dándome la tg∝= 4/3 y como dato que está en el 3er cuadrante. He intentado sacar el coseno pero la solución no coincide con mi resultado.
Me podrían ayudar?


Antonio Silvio Palmitano
el 14/11/16Observa que has cometido un error:
(16/9)y2 + y2 = extraemos factor común = (16/9 + 1)y2 = extraemos denominador común en el agrupamiento:
= ( (16 +9)/9 )y2 = (25/9)y2.
Luego continúas con la identidad:
(16/9)y2 + y2 = 1, resolvemos a la izquierda como hemos hecho más arriba:
(25/9)y2 = 1, hacemos pasajes de factor y divisor:
y2 = 9/25, hacemos pasaje de potencia como raíz:
y = √(9/25), que nos conduce a dos opciones:
a) y = cosα = 3/5, que no corresponde a un ángulo del tercer cuadrante;
b) y = cosα = -3/5, que si corresponde a un ángulo del tercer cuadrante:
Luego puedes continuar con la tarea.
Espero haberte ayudado.
-
Hola! Alguien me podria resolver este ejercicio de fracciones algebraicas? Lo he intentado pero no me sale :( gracias!!


Antonio Silvio Palmitano
el 14/11/16Van orientaciones:
1) Observa que x2 -1 = (x+1)(x-1), por lo que la expresión puede escrobirse:
(x2+1) / (x+1)(x-1) + 5/(x-1) = extraemos denominador común:
= ( x2+1 + 5(x+1) ) / (x+1)(x-1) = distribuimos y reducimos términos semejantes en el numerador:
= ( x2 + 5x + 6 ) / (x+1)(x-1) = factorizamos el numerador (observa que es un polinomio cuadrático):
= (x+2)(x+3) / (x+1)(x-1).
2) Observa que podemos factorizar al polinomio cuadrático x2 - x - 6 = (x+2)(x-3), luego la expresión puede escribirse:
4x/(x+2) + (x-5)/(x-3) - (4x2 - 5x + 8) / (x+2)(x-3) = extraemos denominador común:
= ( 4x(x-3) + (x-5)(x+2) - (4x2 - 5x + 8) ) / (x+2)(x-3) = distribuimos en el numerador:
= ( 4x2 - 12x + x2 + 2x - 5x - 10 - 4x2 + 5x - 8 ) / (x+2)(x-3) = reducimos términos semejantes en el numerador:
= (x2 - 10x - 18) / (x+2)(x-3).
Espero haberte ayudado.