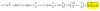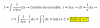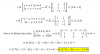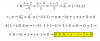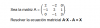-
Desconocido
el 12/11/16El 0.003% de la población muere por una enfermedad desconocida. De 10000 personas, calcula la probabilidad de que 2 o mas murieran por la enfermedad.
El problema que tengo es que no se que distribución tengo que utilizar ya que no voy a poder calcular la factorial de 10000 como es obvio.
-
Alex Gutiérrez
el 12/11/16 -
Alex Gutiérrez
el 12/11/16 -
Dan SaaVi
el 12/11/16¡Hola! He intentado unas cinco veces resolver el siguiente sistema de ecuaciones y cada vez que lo hago, me dan distintos resultados. Agradecería muchísimo que me dijeran cómo resolverla bien. Haha.
Es esta:
6x + 6y = 5
x2 + y2 = 5/36
-
Pablo Reyes
el 12/11/16 -
Jose Manuel
el 12/11/16
Alguien me ayuda con este ejercicio,aunque sea el ejemplo uno para guiarme no se como hacerlo y en el examen no me dejan calculadora
-
anaespo
el 12/11/16 -
Albus99
el 12/11/16Hola, buenas. Querría que me echarais una mano con este ejercicio de geometría del espacio: Determinar el plano que:
a) Pasa por A(1,2,1) y es paralelo a las rectas
r: x+y+2z=0//2x-y-z=0 y s: -x-y+z+1=0//2x-y+2=0
b) Pasa por A (1,-1,3) y perpendicular a la recta r: x-2/-3=y=z-1
Antonio Silvio Palmitano
el 12/11/16a) Tienes el punto A(1,2,1) que pertenece al plano y, como las rectas son paralelas al plano, puedes plantear que un vector normal al plano es igual al producto vectorial entre los vectores directores de las rectas:
n = <1,1,2>x<2,-1,-1> = <1,5,-3>,
luego, la ecuación cartesiana implícita del plano queda: 1(x-1) + 5(y-2) - 3(z-1) = 0, distribuimos, reducimos términos y queda: x + 5y - 3z - 8 = 0.
b) Observa que el plano es perpendicular al vector director de la recta (cuyas componentes son los denominadores en los tres miembros de la doble igualdad en las ecuaciones cartesianas simétricas: (x-2)/(-3) = (y-0)/1 = (z-1)/1), por lo que un vector normal al plano puede ser dicho vector, por lo que tenemos:
n = <-3,1,1>, y como el punto A(1,-1,3) pertenece al plano, tenemos que su ecuación cartesiana implícita queda:
-3(x-1) + 1(y+1) + 1(z-3) = 0, que al distribuir y reducir términos queda: -3x + y + z + 1 = 0.
Espero haberte ayudado.
-
Fernando
el 12/11/16
Don Antonio Garcia espero me puede ayudar con el siguiente problema de álgebra lineal. Gracias de antemano :)
-
Xia
el 12/11/16Duda para ordenar correctamente la ecuación
Antonio Silvio Palmitano
el 12/11/16Observa que A es una matriz cuadrada de orden 3, llamamos I3 a la matriz identidad de orden 3, y podemos escribir la ecuación en la forma:
AX - A = I3 X, hacemos pasajes de términos y queda:
AX - I3 X = A, extraemos factor común a derecha y queda:
(A - I3)X = A, multiplicamos a izquierda en ambos miembros por la matriz inversa de (A - I3) y queda:
(A - I3)-1(A - I3)X = (A - I3)-1A, resolvemos los dos primeros factores en el primer miembro y queda:
I3X = (A - I3)-1A, resolvemos el producto en el primer miembro y llegamos a:
X = (A - I3)-1A.
Solo queda que hagas los cálculos.
Espero haberte ayudado.
Xia
el 12/11/16Muchas gracias por la ayuda!
He calculado los términos (A - I3) y el resultado lo he llamado B suponiendo que no afecta al resultado final de la ecuación matricial.Por tanto sería X = B-1 A
Para hallar la inversa de B utilicé la fórmula B-1=(1/|B|) (B*)t
cuyo resultado fue:
(1 4/3 -2/3)
(0 2/3 -1/3)
(0 1/3 1/3)
Y procediendo al producto de ambas matrices la solución X creo que es:
(2/3 4/3 -2/3)
(-2/3 5/3 -1/3)
(-1/3 1/3 4/3)
