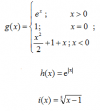-
 Buenas he hecho este ejercicio pero me he quedado ahí porque no me sale bien ni sé cómo seguir ...alguien me puede ayudar?? Gracias!!
Buenas he hecho este ejercicio pero me he quedado ahí porque no me sale bien ni sé cómo seguir ...alguien me puede ayudar?? Gracias!!

Antonio Silvio Palmitano
el 13/11/16Observa al final de la primera línea: la fila 4 es igual a la fila 3, por lo que si a la fila 4 le restas la fila 3 te queda nula la fila 4, lo haces y queda:
1 -2 -2 1 4
0 -1 -3 2 -1
0 -1 -1 0 -2
0 0 0 0 0
luego, a la fila 1 le restas el doble de la fila 2, a la fila 3 le restas la fila 2 y queda:
1 0 4 -3 6
0 -1 -3 2 -1
0 0 2 -2 -1
0 0 0 0 0
luego multiplicas a la fila 2 por -1, a la fila 3 por 1/2 y queda:
1 0 4 -3 6
0 1 3 -2 1
0 0 1 -1 -1/2
0 0 0 0 0
luego, a la fila 1 le restas el cuádruple de la fila 3, a la fila 2 le restas el triple de la fila 3 y queda:
1 0 0 1 8
0 1 0 1 5/2
0 0 1 -1 -1/2
0 0 0 0 0
Observa que ya tienes la matriz reducida y escalonada por filas, y el sistema de ecuaciones equivalente queda:
x + t = 5, de donde tienes: x = -t + 8;
y + t = 5/2, de donde tienes: y = -t + 5/2;
z - t = -1/2, de donde tienes: z = t - 1/2;
0 = 0, que es una identidad verdadera, y como t "ha quedado libre": t ∈ R.
Por lo que concluimos que el sistema es compatible indeterminado y tiene infinitas soluciones, como indican las expresiones remarcadas.
Espero haberte ayudado.
-
Buenos dias ¡ Tengo una duda
Enunciado:
Desde dos puntos A y B situados en la misma orilla de un río y distantes entre sí 80 m, se observa un punto C situado en la orilla opuesta, bajo ángulos de 60º y 45º, respectivamente. Calcula las distancias desde los puntos A y B al punto C.α = 60°, β = 45°, γ = 75°, para los ángulos con vértices A, B y C, respectivamente.
Esto fue lo que hize:
Observo que el lado opuesto al vértice C, le denomino c y que tiene 80m de longitud, nos preguntan las longitudes de los otros dos lados: b (opuesto al vértice B) y a (opuesto al vértice A).
A partir del Teorema del Seno
a) senα / a = senγ / c, de donde puedes despejar a = c*senα / senγ
Reemplaze por el Teorema de Seno y me quedo:
a = 80*sen60°/sen75° A partir de aqui no se como realizar el cálculo.
Un saludo :)
-


Antonio Silvio Palmitano
el 13/11/16En el ejercicio 63, observa que has consignado erróneamente la ecuación polinómica cuadrática, pues has llegado correctamente a la ecuación cuadrática: x2 - 4x2 - 9 + 12x = 3, pero cuando haces pasaje de término, reduces términos semejantes y ordenas queda: -3x2 + 12x - 12 = 0, luego divides por -3 en todos los términos de la ecuación y queda: x2 - 4x + 4 = 0, cuya solución es x = 2 como has consignado. Luego, la solución es x = 2, y = 1, como has consignado correctamente.
En el ejercicio 64 has llegado correctamente a las dos opciones para la incógnita z:
a) z = 18, luego sustituyes y queda: x2 = 18, luego resuelves y tienes dos opciones:
a1) x = +√(18) = +3√(2), que corresponde a y = -1/√(2) = -√(2)/2,
a2) x = -√(18) = -3√(2), que corresponde a y = -1/(-√(2)) = +√(2)/2.
b) z = 1, luego sustituyes y queda: x2 = 1, luego resuelves y tienes dos opciones:
b1) x = 1, que corresponde a y = -3,
b2) x = -1, que corresponde a y = 3.
Por lo tanto, este sistema tiene cuatro soluciones, y es conveniente que las expreses al finalizar la tarea:
x = +3√(2), y = -√(2)/2,
x = -3√(2), y = +√(2)/2
x = 1, y = -3
x = -1, y = 3.
Espero haberte ayudado.
-
- Necesito determinar el supremo y/o el infimo, de este conjunto pero cuando llego al ultimo paso, es decir, los conjuntos, no se muy bien que hacer.
- También hay otro método realizando una grafica y hallando su vertice, pero una vez que lo hallo, tampoco se averiguar el supremo y/o infimo
- Gracias de antemano




Antonio Silvio Palmitano
el 13/11/16Has planteado bien la factorización del primer miembro de la inecuacón, que te ha quedado:
3(x - 3(x - 1/3) < 0, luego divides por 3 en ambos miembros (observa que no cambia el sentido de la desigualdad) y queda:
(x - 3(x - 1/3) < 0, luego tienes dos opciones:
a) x - 3 > 0 y x - 1/3 < 0, que equivalen a: x > 3 y x < 1/3, que nos conduce al intervalo vacío;
b) x - 3 < 0 y x - 1/3 > 0, que equivalen a: x < 3 y x > 1/3, que nos conduce al intervalo: (1/3,3);
por lo tanto, el intervalo solución de la inecuación es: S = (1/3,3).
Luego, para estudiar la existencia de máximo, mínimo, supremo e ínfimo, debemos estudiar la imagen If de la función asociada correspondiente, en el intervalo solución:
f(x) = 3x2 - 10x + 3, observa que su gráfica es una paraábola con vértice mínimo y, para visualizar mejor, buscamos la forma canónica, y para ello planteamos las coordenadas del vértice:
xv = -b/2a, que en este caso queda: xv = 10/6 = 5/3.
yv = c - b2 / 4a, que en este caso queda: yv = 3 - 100/12 = - 16/3.
Luego, la forma conónica de la expresión de la función queda:
f(x) = 3(x - 5/3)2 - 16/3.
Observa que el primer término es positivo, y que se anula para x = 5/3, luego la función toma el valor: f(5/3) = yv = - 16/3 ∈ If.
Luego, evaluamos para los extremos del intervalo (observa que no pertenecen al intervalo:
f(1/3) = 3(1/3 - 5/3)2 - 16/3 = 3(- 4/3)2 - 16/3 = 3(16/9 - 16/3 = 16/3 - 16/3 = 0 ∉ If
f(3) = 3(3 - 5/3)2 - 16/3 = 3(4/3)2 - 16/3 = 3(16/9 - 16/3 = 16/3 - 16/3 = 0 ∉ If.
Luego, observa que la imagen es el intervalo: If = [-16/3,0).
Luego concluimos:
Mínimo en x = 5/3 (al que le corresponde la ordenada y = -16/3),
Ínfimo en x = 5/3 (al que le corresponde la ordenada y = -16/3),
no presenta Máximo,
Supremos en x = 1/3 y en x = 3 (a los que les corresponde la ordenada y = 0).
Espero haberte ayudado.
-
Por favor, necesito ayuda con un límite.
Es este:lim (arctanx-arcsenx)/(x^3)
x->0
Por favor, no necesito resolverlo pro L'Hopital, sino por otros métodos. Muchas gracias. :)


Antonio Silvio Palmitano
el 13/11/16Podemos plantear polinomios de McLaurin para las dos funciones del numerador:
f (x) = arctanx, que evaluada queda: f(0) = 0
f(1)(x) = 1/(1+x2) = (1+x2)-1, que evaluada queda: f(1) (0) = 1
f(2)(x) = - 2x(1+x2)-2, que evaluada queda: f(2)(0) = 0
f(3)(x) = - 2(1+x2)-2 + 8x2(1+x2)-3, que evaluada queda: f(3)(0) = - 2
f(4)(x) = 24x(1+x2)-3 - 48x3(1+x2)-4, que evaluada queda: f(4)(0) = 0
f(5)(x) = 24(1+x2)-3 - 288x2(1+x2)-4 + 388x3(1+x2)-5 , que evaluada queda: f(5)(c1) = a, con c1 entre 0 y x.
Luego, el polinomio de McLaurin para esta función queda (la expresión del resto la abreviamos):
P1(x) = 1x - (2/3!)x3 + Ax5 = 1x - (1/3)x3 + Ax5
g (x) = arcsenx, que evaluada queda: g(0) = 0
g(1)(x) = 1/√(1-x2) = (1-x2)-1/2, que evaluada queda: g(1) (0) = 1
g(2)(x) = x(1-x2)-3/2, que evaluada queda: g(2)(0) = 0
g(3)(x) = (1-x2)-3/2 +3x2(1-x2)-5/2, que evaluada queda: g(3)(0) = 1
g(4)(x) = 9x(1-x2)-5/2 + 15x3(1-x2)-7/2, que evaluada queda: g(4)(0) = 0
g(5)(x) = 9(1-x2)-5/2 + 90x2(1-x2)-7/2 + 105x4(1-x2)-9/2, que evaluada queda: gf(5)(c2) = b, con c2 entre 0 y x.
Luego, el polinomio de McLaurin para esta función queda (la expresión del resto la abreviamos):
P2(x) = 1x - (1/3!)x3 + Bx5 = 1x - (1/6)x3 + Bx5
Luego planteamos el límite, y reemplazamos las expresiones en el numerador por sus desarrollos de McLaurin:
lim (arctanx-arcsenx)/x3 = lim ( P1(x) - P2(x) )/x3 =
x->0
sustituimos las expresiones de los desarrollos de McLaurin
= lim ( 1x - (1/3)x3 + Ax5 - 1x + (1/6)x3 - Bx5 )/x3 =
x->0
reducimos términos semejantes, y queda:
= lim (- (1/6)x3 + (A - B)x5 )/x3 =
x->0
distribuimos el denominador, simplificamos y queda:
= lim (- 1/6 + (A - B)x2 ) = resolvemos = -1/6.
x->0
Espero haberte ayudado.
-
Hola por favor necesito ayuda con derivada parcial de la siguiente funsion :
F(x,y) = 40 x 3/4 y 1/4 me complica la franccion
-
Hola,
me piden estudiar la derivabilidad de las siguientes funciones y calcular la expresión de la función derivada:
¿Están bien hechos?
Gracias


Antonio Silvio Palmitano
el 13/11/16En el ejercicio a), observa que la función toma el valor 1 para x = 0, por lo que se trata de un punto aislado y no le planteamos límite y solo indicamos: f(0) = 1, luego los límites laterales los has planteado y resuelto bien.
En lo que se refiere a la derivabilidad, la derivada de la función en x = 0 debe ser planteada según la definición y, como se trata de un punto de corte, deberemos plantear los límites laterales del cociente incremental:
Lím(h-->0+) ( f(0+h) - f(0) )/h = Lím(h-->0+) ( f(h) - 1 )/h = Lím(h-->0+) (eh - 1)/h = (regla de L'Hôpital) = Lím(h-->0+) eh/1 = 1
Lím(h-->0-) ( f(0+h) - f(0) )/h = Lím(h-->0) ( f(h) - 1 )/h = Lím(h-->0) ( h2/2 + 1 + h - 1 )/h = Lím(h-->0-) ( h(h/2 + 1) )/h = Lím(h-->0-) (h/2 + 1) = 1
Luego, como las derivadas laterales coinciden, concluimos que f ' (0) = 1.


Antonio Silvio Palmitano
el 13/11/16En el ejercicio b) has mostrado bien que la función h(x) = e|x| es continua, y que los límites de las derivadas laterales no coinciden para x = 0, por lo que h ' (x) no está definida en dicho punto.
Por lo tanto concluimos que la función es continua en R, y derivable en R - {0}.
En el ejercicio c) tienes que la función i(x) = 5√(x - 1) tiene dominio R, y la expresión de su función derivada es: i ' (x) = 1 / ( 5 5√( (x - 1)4 ) ).
Observa que la función está definida y es continua en x = 0, pero la expresión de su derivada se indetermina en dicho punto, por lo que planteamos su derivada con la definición:
Lím(h-->0)( i(0+h) - i(0) )/h = Lím(h-->0)( 5√(h - 1) - 5√(0 - 1) )/h = Lím(h-->0)( 5√(h - 1) - 5√( - 1) )/h = Lím(h-->0)
= Lím(h-->0)( 5√(h - 1) + 1 )/h = (regla de L'Hôpital) = Lím(h-->0)( 1 / ( 5 5√( (h - 1)4 ) ) )/1 = infinito.
(Observa que este último límite podría haberse planteado en forma algebraica, pero no lo hicimos porque es un planteo muy largo y tedioso9.
Por lo tanto, concluimos que la función es continua en R, y derivable en R - {0}.
Espero haberte ayudado.
-
Tengo este ejercicio
Para construir la matriz de la transformacion use una base canonica de R4 (Creo que es asi)
T(1,0,0,0)=(1,0,1)
T(0,1,0,0)=(-2,1,1)
T(0,0,1,0)=(1,-3,0)
T(0,0,0,1)=(3,0,-1)
Entonces las columnas de la MT serian el (1,0,1),(-2,1,1),(1,-3,0),(3,0,-1)
Creo que hasta aca estoy bien.
Ahora la pregunta que dice que representa cada columna, supongo que representa la imagen de la base canonica dada (no tengo idea, creo que es asi), luego tengo un problema con el rango.
Se que el rango es el numero de filas o columnas que son linealmente independientes. Se que el rango fila y columna coinciden pero me resulta complicado en una matriz de 3x4 comprobar si cada columna es linealmente independiente. No puedo usar determinantes porque no me lo enseñaron todavia, creo que tengo que usar combinacion lineal. Seria asi?
Porque necesito sacar el numero de columnas linealmente independientes para luego dar una base de la imagen de MT.


Antonio Silvio Palmitano
el 13/11/16Has expresado bien cómo construir la matriz asociada a la transformación lineal. Luego, debes precisar que cada columna de la matriz MT representa las imágenes de cada uno de los vectores de la base canónica, que es la que empleaste en este ejercicio.
Luego, recuerda que el rango puede ser, a lo sumo, igual al mínimo entre las cantidades de filas y de columnas de la matriz.
Tenemos la matriz asociada a la transformación lineal (observa que hemos dispuesto las columnas tal como has dicho):
1 -2 1 -3
0 1 -3 0
1 1 0 -1
a la fila 3 le restamos la fila 1 y queda:
1 -2 1 -3
0 1 -3 0
0 3 -1 2
a la fila 1 le sumamos el doble de la fila 2, a la fila 3 le restamos el triple de la fila 2 y queda:
1 0 -5 -3
0 1 -3 0
0 0 8 2
multiplicamos a la fila 3 por 1/8 y queda:
1 0 -5 -3
0 1 -3 0
0 0 1 1/4
a la fila 1 se sumamos 5 veces la fila 3, a la fila 2 le sumamos el triple de la fila 3 y queda:
1 0 0 -7/4
0 1 0 3/4
0 0 1 1/4
luego, como hemos llegado a la matriz reducida y escalonada por filas, concluimos que el rango de la matriz es 3.
Observa que si hubiese sido necesario, podríamos haber traspuesto la matriz. Observa también que como teníamos menos filas que columnas no fue necesario trasponer (recuerda que el rango de una matriz es igual al rango de su matriz traspuesta).
Espero haberte ayudado.