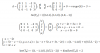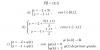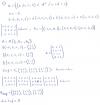-
- Me pueden enseñar a hacer la gráfica, hallando máximos y minimos de esta función:. f(x)=2cos(x)-cos(2x), x∈ [-π,π]


Antonio Silvio Palmitano
el 12/11/16Debes tener en cuenta las identidades trigonométricas: cos(2x) = cos2x - sen2x (*), también: sen(2x) = 2senxcosx (**), y también: sen2x = 1 - cos2x (***).
Luego, tienes la función cuya expresión es:
f(x) = 2cosx - cos(2x), con x ∈ [-π,π], aplicas la identidad señalada (*) y queda: f(x) = 2cosx - cos2x + sen2x, aplicas la identidad señalada (***) y queda: f(x) = 2cosx - 2cos2x + 1.
luego, la expresión de la derivada primera queda:
f ' (x) = -2senx + 2sen(2x), aplicas la identidad señalada (**) y queda: f ' (x) = -2senx + 4senxcosx, extraes factor común y queda: f ' (x) = 2senx(-1+2cosx);
luego la expresión de su derivada segunda queda:
f ' ' (x) = -2cosx + 4cos(2x), aplicas la identidad señalada (*) y queda: f ' ' (x) = -2cosx + 4cos2x - 4sen2x,
luego aplicas la identidad señalada (***) y queda: f ' ' (x) = -2cosx + 8cos2x - 4.
Luego pasamos al estudio de la gráfica de la función:
1) Intersecciones con el eje OX:
f(x) = 0, sustituyes y queda la ecuación: 2cosx - 2cos2x + 1 = 0, que se resuelve con el cambio de incógnita: t = cosx (queda para que continúes la tarea).
2) Intersecciones con el eje OY:
f(0) = 2 - 2 + 1 = 1, que corresponde al punto A(0,1).
3) Valores de la función en los extremos del intervalo cerrado:
f(-π) = -2 - 2 + 1 = -3, que corresponde al punto B(-π,-3)
f(π) = 2 - 2 + 1 = 1, que corresponde al punto C(π,1).
4) Puntos críticos o singulares:
f ' (x) = 0, sustituyes y queda la ecuación: 2senx(-1+2cosx) = 0, resuelves y queda: x = -π, x = 0, x = π, x = π/6, x = 5π/6 (queda para que verifiques).
5) Posibles puntos de inflexión:
f ' ' (x) = 0, sustituyes y queda la ecuación: -2cosx + 8cos2x - 4 = 0, que puedes resolver con el cambio de incógnita: t = cosx (queda para que continúes la tarea).
Como verás, debes continuar trabajando, y debes tener en cuenta identidades y métodos de resolución para resolver ecuaciones trigonométricas.
Espero haberte ayudado.
-
Hola unicoos necesito ayuda con una ecuación diferencial. Gracias! X.Y ' - Y2 = X.Y2


Antonio Silvio Palmitano
el 12/11/16Puedes intentar separar variables:
xy ' - y² = xy², haces pasaje de término y queda:
xy ' = xy² + y², extraes factor común en el segundo miembro, sustituyes y ' = dy/dx, y queda:
xdy/dx = (x+ 1)y², haces pasajes de divisores y factores y queda:
dy/y² = (x + 1)dx/x, distribuyes el denominador en el segundo miembro y queda:
y-2dy = (1 + 1/x)dx, luego integras miembro a miembro y queda:
- y-1 = x + ln|x| + C, que es una solución general implícita para esta ecuación diferencial.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 13/11/16Entonces, como el plano buscado es perpendicular a dos planos conocidos, puedes plantear que un vector normal al plano Π0 puede ser el producto vectorial entre los vectores normales a los planos Π4 y Π5:
n0 = n4 × n5 = <-1,1,1> × <1,-2,1> = <3,2,1>.
Luego, como tienes que el punto de intersección entre las rectas L2 y L3 pertenece al plano, puedes igualar a partir de sus ecuaciones vectoriales paramétricas:
<-3,-6,8> + t2<3,-1,3> = <-5,-6,9> + t3<1,-1,4>, luego haces pasajes de términos, resuelves en el segundo miembro y queda:
t2<3,-1,3> - t3<1,-1,4> = <-2,0,1>, luego planteas ecuaciones igualando componente a componente, y queda el sistema:
3t2 - t3 = -2
-t2 + t3 = 0
3t2 - 4t3 = 1
Observa que tienes tres ecuaciones con dos incógnitas, resuelves el sistema (te dejo la tarea) y verás que la solución es: t1 = -1, t2 = -1, luego reemplazas en las ecuaciones vectoriales de las rectas, y verás que el punto de intersección tiene coordenadas: A(-6,-5,5) ∈ Π0.
Luego, ya tienes todo para plantear una ecuación para el plano buscado.
A(-6,-5,5) ∈ Π0
n0 = <3,2,1>
Luego, planteamos la ecuación vectorial del plano buscado:
<3,2,1> • < x+6 , y+5 , z-5 > = 0.
Luego desarrollamos el producto escalar, reducimos términos numéricos, y llegamos a la ecuación cartesiana paramétrica implícita del plano buscado:
3x + 2y + z + 23 = 0.
Espero haberte ayudado.
-
Como hacer este ejercicio?
No se como hallar el nucleo. Tengo que la respuesta a este ejercicio es Nu TA = ⟨ (−1, 3, −1, 1, 0) , (−1, −11, 8, 0, 1) ⟩ osea una base de 2 pero por mas que lo intento no logro dar con ese resultado. Hay alguna forma de hacerlo y verificar que este bien?.
-


Antonio Silvio Palmitano
el 12/11/16a) Consideras como vector director la vector aplicado en el primer punto, con extremos en el último: u = PQ = <5,1>, luego con este vector y el primer punto P(-2,-1), puedes plantear las ecuaciones cartesianas paramétricas:
x = -2 + 5t
y = -1 + t
con 0 ≤ t ≤ 1
Observa que la longitud del intervalo paramétrico es La = 1-0 = 1.
b) Observa que la longitud del nuevo intervalo paramétrico es Lb = 1-(-1) = 2, que es el doble de la longitud del intervalo anterior, que la trayectoria comienza en el punto P como en el ejercicio anterior, y que el primer valor que toma el parámetro es -1, por lo que planteamos:
0 ≤ t ≤ 1, que es el intervalo del ejercicio anterior, multiplicamos por 2 en los tres miembros de la doble desigualdad y queda:
0 ≤ 2t ≤ 2, restamos 1 en los tres miembros de la doble desigualdad y queda:
-1 ≤ 2t - 1 ≤ 1, luego hacemos una sustitución (cambio de parámetro): u = 2t - 1, de donde despejamos y tenemos: (1/2)u + 1/2 = t,
y cuyo intervalo paramétrico es -1 ≤ u ≤ 1.
Luego sustituimos en la parametrización del ejercicio anterior y queda:
x = -2 + 5( (1/2)u+ 1/2 ) = -2 + (5/2)u + 5/2 = 1/2 + (5/2)u
y = -1 + (1/2)u + (1/2) = -1/2 + (1/2)u
por lo tanto, la nueva parametrización queda:
x = 1/2 + (5/2)u
y = -1/2 + (1/2)u
con -1<= u <= 1.
c) Para cambiar el sentido de recorrido, una de las formas es proponer la sustitución (cambio de parámetro) w = - t, de donde tenemos: t = -w, y el intervalo paramétrico queda:
0 <= t <= 1, multiplicamos por -1 en los tres miembros de la doble desigualdad (observa que cambia el sentido de las desigualdades):
0 >= -t >= -1, sustituimos, leemos de derecha a izquierda y queda:
-1 <= u <= 0.
Luego sustituimos en la parametrizacióm del primer ejercicio y queda:
x = -2 - 5w
y = -1 - w
con -1 <= w <= 0.
Espero haberte ayudado.
-
Tengo una duda con un sistema de ecuaciones.
Se me pide que de una base de este sistema de ecuaciones pero no logro poder expresar 3 incognitas en funcion de solamente 2.
y+z-2w+3u=0
2x+y-w+u=0
x-z+3u=0
De este sistema me tiene que quedar una base de dimension 2. Pero trato de despejar los terminos en funcion de los otros para crear una base y no me sale.


Antonio Silvio Palmitano
el 13/11/16Va una ayuda para la resolución del sistema de ecuaciones.
Observa que tienes tres ecuaciones con cinco incógnitas, por lo que, a lo sumo, podremos despejar tres incógnitas que nos quedarán en funciones de las otras dos.
Tenemos el sistema:
y+z-2w+3u=0, de aquí podemos despejar: y = -z + 2w - 3u (*)
2x+y-w+u=0
x-z+3u=0
luego sustituimos la expresión señalada (*) en las otras dos ecuaciones, reducimos términos semejantes y queda el sistema:
2x + w - 2u = 0, de aquí podemos despejar: w = -2x + 2u (**)
x - z + 3u = 0, de aquí podemos despejar x + 3u = z (***)
luego sustituimos la expresión señalada (***) en la ecuación señalada (*), reducimos términos semejantes y queda: y = -x + 2w - 6u (****),
luego sustituimos la expresión señalada (**) en la ecuación señalada (****), reducimos términos semejantes y queda: y = -5x -2u (*****).
Luego, concluimos que el sistema de ecuaciones tiene infinitas soluciones (empleamos las ecuaciones remarcadas):
x ∈ R
y = -5x -2u
z = x + 3u
w = -2x + 2u
u ∈ R.
Espero haberte ayudado.
-
Hola! Tengo una duda sobre un ejercicio de derivadas implícitas.
El ejercicio me pide que compruebe que sen(x2·y)-y2+x=2-(π2/6) pasa por el punto (2, π/4) y que encuentre la ecuación de la recta tangente en este punto.
El problema que tengo es que no se como aislar la y'. Me podríais ayudar? Gracias!!
-
Hola, ¿alguien podría decirme si el apartado c del siguiente ejercicio está bien resuelto?
Mi solución es:
Un saludo, gracias!


David
el 13/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas.
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)