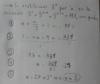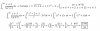Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

DueFreitas
el 9/11/16

profe como se demuestra.

••0 voto/s
•
Antonio Silvio Palmitano
el 9/11/16
Por favor, consulta con tus docentes, porque es muy posible que haya error de redacción en el enunciado del ejercicio 2.

•0 voto/s
•
David
el 10/11/16
(y-k)²=4p(x-h)... Desarrollada... y²+k²-2ky = 4px-4ph... y²-2ky +k²-4px+4ph... Resolviendo la ecuacion de segundo grado... y=[2k+√((2k)²-4.1.(k²-4p.x+4ph))]/2
Para x=xo... yo=[2k+√((2k)²-4.1.(k²-4p.xo+4ph))]/2

Por otro lado, si derivamos implicitamente.... 2y.y' -2k.y' = 4p... y'.(2y-2k)=4p... y'=2p/(y-k)... La pendiente será m=y`(xo)=2p/(yo-k)

La ecuacion de la recta tangente es y-yo=m.(x-xo)..... Sustituye lo obtenido...

Espero te sirva de guía. No puedo ayudarte mucho más, lo siento. tu duda es universitaria y unicoos por ahora se queda en bachiller.

•0 voto/s
•

Cancelar
Ignacio
el 9/11/16

Como transformo una matriz de 4x4 en una de 3x3? Por ejemplo me dan una matriz y me piden que deduzca cuando esa matriz no tiene inversa.

••1 voto/s
•
chado
el 9/11/16
si quisieras transformarlas necesitarias alguna ley de asignacion para hacer la transformacion o datos de la base o algo,
pero si lo que queres es saber si la matriz tiene inversa calculas la determinante, si te da 0 es que la matriz no tiene inversa

•0 voto/s
•
Daniel Arenas
el 9/11/16
No tienes que transformar la matriz 4x4 en una 3x3 para deducir si tiene o no inversa

•0 voto/s
•

Cancelar
Jordi García
el 9/11/16

¿Hola UNICOOS, me podéis ayudar en este ejercicio?

3^x + 3^x-1 + 3^x+1 = 117

He hecho esto pero creo que está mal.
3^x + 3^x-1 + 3^x+1 = 3² * 3^{log3 13}
x + x-1 + x+1 = 2 * log₃ 13
3x = log₃ 169
x = (log₃ 169) / 3 = 1.556

Gracias

••0 voto/s
•
Hugo
el 9/11/16
3x + 3x-1 + 3x+1 = 117
3^x + 3^x / 3 + 3*3^x = 117
3^x (1+ 1/3 + 3) = 117
3^x ( 13/3 ) = 117
3^x = 3*117 / 13

log 3^x = log (3*117 / 13)
x * log3 = log (3*117 / 13)
x = log (3*117 / 13) / log 3

•0 voto/s
•
Antonius Benedictus
el 9/11/16
117=13*9
3^x = (3*117()/13
3^x=27
x=3

•1 voto/s
•
Ángel
el 10/11/16
Otra forma:

•0 voto/s
•

Cancelar
Raquel
el 9/11/16

Como se hace esta integral ? Cual es su procedimiento? Gracias

••0 voto/s
•
Hugo
el 9/11/16
Separala en dos integrales...

∫ sen²(x) / cos²(x) dx = ∫tg²(x) dx = ∫ tg² + 1 -1 dx = ∫ sec²dx - ∫dx termina..
∫ cos²(x) / cos²(x) dx = ∫dx termina..

•0 voto/s
•
Antonio Silvio Palmitano
el 9/11/16
Observa que en el numerador del argumento de la integral tienes: cos²x + sen²x = 1, por identidad trigonométrica fundamental.
Luego, la integral queda:
∫ ( (sen²x + cos²x)/cos²x )dx = ∫ (1/cos²x)dx = tanx + C.
Observa que en el último paso tienes una integral directa.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Ignacio
el 9/11/16

Como se calcula la inversa de una matriz de orden 2x3 por determinantes?

••0 voto/s
•
Antonius Benedictus
el 9/11/16
Las matrices que no son cuadradas NO TIENEN INVERSA.

•0 voto/s
•

Cancelar
I'm a your worse nightmare
el 9/11/16

Hola me podeís ayudar con este ejercicio, por favor muchas gracias. Un saludo y buenas tardes a todos los que están ahí.

••0 voto/s
•
Antonius Benedictus
el 9/11/16

•0 voto/s
•

Cancelar
Antonella
el 9/11/16

Hola buenas tardes, perdón por las molestias, quería saber si me pueden ayudar con estos ejercicios, si me pueden dar algunos tips como para tener en cuanta a la hora de hacerlos, porque estoy estudiando para el examen de calculo 1 estoy un poco perdida, gracias

••0 voto/s
•
chado
el 9/11/16
pero podrias ser mas especifica con la duda? osea, que es lo que no entenderias, asi te podemos ayudar de mejor manera.

•0 voto/s
•

Cancelar
Desconocido
el 9/11/16

F ≡ "El autobús tiene un fallo". La probabilidad de que un autobús tenga un fallo es 2/5.
Se escogen 5 autobuses al azar. Cual es la probabilidad de que 4 de los autobuses tengan un fallo?
Primero sabemos que P(F)=0.4
No tengo claro que formula tengo que aplicar, he pensado en esto:
P(F1 ∩ F2 ∩ F3 ∩ F4 ∩ noF5), pero claro, no tiene porque ser el quinto autobús el que no tenga ningún fallo no? No se si influye el orden...

••0 voto/s
•
Antonio Silvio Palmitano
el 9/11/16
Observa que tienes una distribución binomial (o de Bernoulli), con parámetros: n = 5, p = 0,4, q = 1 - p = 0,6.
Luego, la variable X: "cantidad de autobuses con fallos" puede tomar los valores 0, 1, 2, 3, 4, 5, y tenemos que plantear:
P(X=4) = C(5,4) * 04^4 * 0,6^1 = 5*0,0256*0,6 = 0,0768.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
paco meirinho
el 9/11/16
hola me gustarías saber como puedo demostrar la siguiente
I_n= ∫uⁿ√(a²-u²)* du = (1/n+2)u^n-1(a²-u²)^3/2- (n-1/n+1)a²I_n-2
_{si aplico metodo por}sustitución_{me da lo siguiente}

∫ƒ(g(x))*g'(x)dx= ∫ƒ(u)du
u= g(x) v =uⁿdv = nu^n-1du sustituir v=uⁿ
1. dv/du=nu^n-1
d/du(uⁿ)
llego luego a

∫v √(a²-u² *u^1-n/n)dv

pero no se que hago mal o como demostrar bien el ejercicio
••0 voto/s
•
David
el 10/11/16

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Emi Milesci
el 9/11/16

Hola a todos! Necesito que me ayudeis con estas integrales. Tengo exámen mañana y no entiendo nada

••0 voto/s
•
Antonius Benedictus
el 9/11/16
Emi, creo que lo llevas claro...
Te mando la 1ª integral, como señal de buena voluntad.

•0 voto/s
•

Cancelar