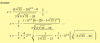Responde esta pregunta...

Regla de tres compuesta #nosvemosenclase

muchas gracias por tu ayuda y por tu gran labor

Responde esta pregunta...

Si pone p>1, entonces 1-p<0, por lo que u^(1-p)=1/(u^(p-1))=1/(+inf)=0

Para el primer problema, por favor envía una foto.

Para el segundo, si los dos motoristas parten desde el punto de bifurcación, llamamos t al tiempo transcurrido en sus viajes, y tenemos para las distancias que han recorrido:

para el primero: d1 = 90t, y como viajó t = 1/2 hora, tenemos: d1 = 30*(1/2) = 15;

para el segundo: d2 = 120t, y como viajó t = 1/2 hora, tenemos: d2 = 120*(1/2) = 60.

luego, el ángulo comprendido entre sus dos distancias es α = 60°, y con la expresión del Teorema del Coseno, podemos plantear (llamamos d a la distancia entre los puntos en que se encuentran los motoristas transcurrida media hora desde su partida desde la bifurcación de carreteras):

d² = d1² + d2² - 2*d1*d2*cosα, reemplazamos valores y queda:

d² = 15² + 60² - 2*15*60*cos60°, resolvemos términos y queda (recuerda que cos60° = 1/2):

d² = 225 + 3600 - 900, resolvemos términos numéricos y queda:

d² = 2925, hacemos pasaje de potencia como raíz y queda:

d = √(2925)

d ≅ 54,083 Km.

Espero haberte ayudado.

Recuerda que los argumentos de raíces de índice par deben ser mayores o iguales que cero, y que los denominadores deben ser distintos de cero.

1) 2x - 3 ≥ 0, donde despejamos: 2x ≥ 3, y luego: x ≥ 3/2, por lo que el dominio para esta expresión queda: D1 = [0,+inf).

2) 4 - 10x ≥ 0, de donde despejamos: - 10x ≥ - 4 y luego (recuerda que pasamos un factor negativo como divisor): x ≤-4/(-10), resolvemos y queda: x ≤ 2/5,

por lo que el dominio para esta expresión queda: D2 = (-inf,2/5].

3) x(x - 5) ≥ 0, que nos conduce a dos opciones (ambos factores positivos o ambos negativos):

a) x ≥ 0 y x - 5 ≥ 0, que cumplen a la vez: x ≥ 0 y x ≥ 5, por lo que el subdominio para esta opción es: [5,+inf),

b) x ≤ 0 y x - 5 ≤ 0, que cumplen a la vez: x ≤ 0 y x ≤ 5, por lo que el subdominio para esta opción es: (-inf,0],

por lo que el dominio para esta expresión queda: D3 = (-inf,0] u [5,+inf).

4) Observa que la raíz cuadrada está en el denominador, por lo que planteamos (observa que no puede tomar el valor cero):

x + 2 > 0, de donde despejamos: x > -2, y el dominio para esta expresión queda: D4 = (-2,+inf).

Espero haberte ayudado. 

Observa que los vértices son los puntos: A1(0,4) y A2(0,-4), que pertenecen al eje de ordenadas OY, que es el eje focal, y son simétricos con respecto al punto O(0,0) que es, por lo tanto, el centro de simetría de la hipérbola, y la longitud del semieje real queda: |OA1| = |OA2| = a = 4.

Observa que la expresión de la excentricidad es: exc = c/a, reemplazamos y queda: 3/2 = c/4, de donde despejamos: 6 = c.

Luego, a partir de la relación entre semiejes en las hipérbolas, tenemos: b² = c² - a², reemplazamos y queda: b² = 6² - 4², resolvemos y queda: b² = 20, de donde tenemos: b = V(20).

Luego, planteamos la ecuación cartesiana canónica para esta hipérbola con eje focal OY y centro de simetría O(0,0):

- x²/b² + y²/a² = 1, reemplazamos, resolvemos denominadores y queda: - x²/20 + y²/16 = 1.

Espero haberte ayudado.

Responde esta pregunta...

Pero profe es una ecuación cubica,¿ como se obtiene las demás soluciones?

Vamos con una orientación.

Tienes que construir tres tramos: base, pared y tapa, para los que planteamos sus áreas y sus costos:

Para la base (disco plano circular): Ab = πr², cuyo costo será: Cb = 5πr².

Para la pared (cilindro circular): Ap = 2πrh, cuyo costo será: Cp = 8*2πrh, resolvemos factores numéricoss y queda: Cp = 16πrh.

Para la tapa (semiesfera): At = (1/2)4πr², cuyo costo será: Ct = 20*(1/2)4πr², resolvemos factores numéricos y queda: Ct = 40πr².

Luego, planteamos el costo total, que será función del radio del cilindro (y de la semiesfera), y la altura del cilindro, como la suma de los tres costos parciales, y queda la función:

C(r,h) = 5πr² + 16πrh + 40πr², reducimos términos semejantes y la expresión de la función queda:

C(r,h) = 45πr² + 16πrh.

Luego, la restricción que plantea el problema es que el volumen del tanque debe ser 200π, por lo que tenemos que el volumen es la suma entre los volúmenes del pedazo cilíndrico y del pedazo semiesférico del tanque, por lo que tenemos:

Para el pedazo cilíndrico: Vc = πr²h.

Para el pedazo semiesférico: Vs = (1/2)(4/3)πr³, resolvemos factores numéricos y queda: Vs = (2/3)πr³.

Luego, el volumen del tanque queda expresado como función de r y de h:

V(r,h) = πr²h + (2/3)πr³ = 200π.

Luego, debes continuar con el planteo del sistema de ecuaciones de Lagrange, que queda:

90πr + 16πh = λ(2πrh + (2/3)*2πr)

16πr = λπr²

πr²h + (2/3)πr³ = 200π

Dividimos por 2π y multiplicamos por 3 en la primera ecuación, dividimos por π en la segunda, multiplicamos por 3 y dividimos por π en la tercera y el sistema queda:

135r + 24rh = λ(3rh + 12r)

16r = λr²

3r²h + 2r³ = 600.

Luego, queda para que resuelvas este sistema de ecuaciones, y observa que puedes comenzar por la segunda ecuación, que luego de un pasaje de término queda:

16r - λr² = 0, factorizas y queda:

r(16 - λr) = 0, lo que conduce a dos opciones, que deberás considerar por separado:

a) r = 0, que no tiene sentido para este problema (observa que r es el radio del cilindro y de la semiesfera, por lo que debe ser estrictamente positivo).

b)16 - λr  = 0, de donde puedes despejar (recuerda que r no puede ser igual a cero): 16/r = λ, luego sustituyes en las otras dos ecuaciones y el sistema queda:

135r + 24rh = (16/r)(3rh + 12r)

3r²h + 2r³ = 600

Observa que puedes distribuir en la primera ecuación, y luego continuar la tarea.

Espero haberte ayudado.

Considera un sistema cartesiano con eje OX al nivel del suelo, y eje OY coincidente con el eje de simetría de la parábola, lo haces y tienes:

vértice: V(0,25),

cortes con el eje OX: A1(-20,0), A2(20,0).

Luego puedes plantear la ecuación canónica de una parábola con eje vertical, con vértice en el punto que hemos indicado:

(x - 0)² = 4c(y - 25) (*).

Luego, puedes reemplazar las coordenadas de uno de los puntos que tenemos (lo hacemos con A2) y queda:

(20 - 0)² = 4c(0 - 25), resolvemos factores y quda:

400 = -100c, despejamos y queda:

-4 = c.

Luego, reemplazamos en la ecuación señalada (*) y queda:

(x - 0)² = 4*(-4)(y - 25), cancelamos término nulo, resolvemos factores numéricos y queda:

x² = - 16(y - 25).

Luego, para los puntos con abscisa x = ± 8 tenemos:

(± 8)² = -16(y - 25), resolvemos términos, distribuimos y queda:

64 = - 16y + 400, hacemos pasajes de términos, reducimos términos semejantes y queda:

16y = 336, hacemos pasaje de factor como divisor y queda:

y = 336/16, resolvemos y llegamos a:

y = 21, que es la altura de ambos puntos con respecto al nivel del suelo.

Espero haberte ayudado.

Has planteado y resuelto todo correctamente.