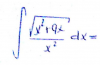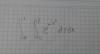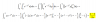-
Jose Manuel
el 4/11/16
No tengo ni idea de como se resuelve el siguiente ejercicio,todo me male sal
-
Usuario eliminado
el 4/11/16 -
Celia
el 4/11/16Me podeis ayudar con estos ejercicios? no me salen las soluciones...
1.-Hallar el volumen de un cuerpo contenido en el primer octante acotado por los planos coordenados y por z=2x^2+y^2+1, x+y=1. Solucion=3/4. Me sale 5/6...
2.- Integrar f(x,y)=abs(y-senx) en el conjunto D=[0,pi]x[0,pi], tiene que dar pi-2, y al hacer la integral doble me sale pi^2.
Gracias!
-
Víctor Miranda
el 4/11/16 -
Nuria
el 4/11/16
¿POR QUÉ? si el dominio de los logaritmos neperianos debe ser los numeros mayores que 0...Samuel
el 4/11/16
Antonio Silvio Palmitano
el 4/11/16Debes tener en cuenta que las funciones logarítmicas son las funciones inversas de las exponenciales.
Recuerda que definimos a una función exponencial mediante la expresión:
f(x) = a^x, con a > 0 y a ≠ 1,
y como seguramente has estudiado en clase tienes que las funciones exponenciales son continuas en todo R, y que son:
estrictamente crecientes, si la base a es mayor que uno, y
estrictamente decrecientes si la base a está comprendida estrictamente entre 0 y 1.
Recuerda que el dominio de las funciones exponenciales es R, y que su imagen es el intervalo (0,+inf).
Por lo tanto, el dominio de las funciones inversas de las exponenciales, que son las funciones logarítmicas, tienen:
dominio: D = (0,+inf) (que coincide con la imagen de la funciones exponenciales),
imagen: I = (-inf,+inf) = R (que coincide con el dominio de las funciones exponenciales),
y son continuas en su dominio D.
Luego, para el ejercicio de la imagen, has elegido la opción correcta: el dominio de la función es R, y la función es continua en R, porque:
la expresión x(x+1) corresponde a una función continua en R, luego:
la expresión: e^(x(x+1)) corresponde a una función continua en R, porque es composición de la función polinómica con la función exponencial natural, que son ambas continuas, luego:
la expresión: e^(x(x+1)) + 2 corresponde a una función continua en R porque es suma de expresiones de funciones continuas en R, y observa que los valores que toma pertenecen al intervalo (2,+inf), cuyos elementos son todos estrictamente positivos, luego:
la expresión de la función: f(x) = ln(e^(x(x+1)) + 2) indica que f es una función continua, ya que es composición de funciones continuas, y observa que el logaritmo natural puede ser evaluado para todo valor de x, ya que su argumento es estrictamente mayor que cero.
Espero haberte ayudado.
-
Samuel
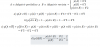
el 4/11/16Muy buenos días unicoos. ¿Alguno de vosotros sabría explicarme por qué el rango de una matriz A no varía al multiplicarlo por una matriz invertible(es decir; rg(A)=rg(BA))? Si pudierais ponerme un ejemplo mejor que mejor. Gracias de antemano
-
Nuria
el 4/11/16
Quiero calcular (f o g).
Antonio Silvio Palmitano
el 4/11/16Observa que el dominio de la función f es: Df = (-1,+inf), y que su Imagen es: If = (-inf,+inf) = R.
Observa que el dominio de la función g es: Dg = (-inf,+inf), y que su imagen es: Ig = (-1,+inf).
Luego, planteamos la función "g compuesta con f".
(f o g)(x) = f( g(x) ) = f( e^(2x-1) - 1 ) = ln( 1 + e^(2x-1) - 1 ) = ln( e^(2x-1) ) = 2x - 1.
Observa que los elementos g(x) pertenecen todos al dominio de la función f, por lo que tenemos para la función compuesta:
dominio: D = Dg = (-inf,+inf), imagen: I = If = (-inf,+inf).
Espero haberte ayudado.
-
Daniel
el 4/11/16 -
Mario Peña
el 4/11/16Buen día me gustaría saber como resolver este ejercicio mediante la aplicación de la hipérbola, lo intenté planteando relación de triángulos pero no llego a la solución, muchas gracias!! (La solución del ejercicio es( ((80)/(3)) sqrt(34 ) , 100)
Antonio Silvio Palmitano
el 4/11/16Ubica el origen de coordenadas en el punto medio entre las dos estaciones, y los focos en cada estación. Tienes:
F1(-100,0), ubicado en la Estación A, F2(100,0), ubicado en la Estación B, por lo que la longitud del semieje focal queda: c = 100.
Luego, tienes que la diferencia entre las distancias entre el punto P(x,y) (observa que y = 100) (*), que coincide con la ubicación del barco, y los focos F1 y F2 es igual a 160, por lo que tienes:
d(P,F1) - dP(F2) = 2a = 160, por lo que la longitud del semieje real queda: a = 80.
Luego puedes plantear la relación entre las longitudes de los semiejes de una hipérbola: b² = c² - a², reemplazas y queda:
b² = 100² - 80² = 10000 - 6400 = 3600 = 60², de donde tienes: b = V(3600) = 60, que es la longitud del semieje imaginario.
Luego, la ecuación de la hipérbola (observa que tiene eje real sobre el eje coordenado OX) queda:
x²/80² - y²/60² = 1.
Luego reemplazamos las ordenada del punto P en la ecuación de la hipérbola, según la igualdad señalada (*), y queda:
x²/80² - 100²/60² = 1, resuelves a la izquierda:
x²/6400 - 25/9 = 1, haces pasaje de término, resuelves a la derecha y queda:
x²/6400 = 34/9, haces pasaje de divisor como factor, y queda:
x² = 6400*34/9, haces pasaje de potencia como raíz, distribuyes a la derecha, resuelves factores racionales y queda:
x = 80*V(34)/3 = 155,49 (aproximadamente),
por lo que concluimos que el barco está ubicado en el punto de coordenadas: P(80*V(34)/3,100).
Espero haberte ayudado.
