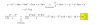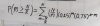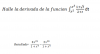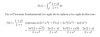Lo siento pero no entiendo tu pregunta. Si nos envías algun ejemplo...

Te explicamos, Facundo:

¿Y de qué se trata, Robin?

Llamemos D al vértice inferior, que se encuentra en la misma cara que los vérticea A y C (que está incluida en el plano de ecuación x = -3), y observa que sus coordenadas son: D(-3,1,4).

Llamemos B al tercer vértice del triángulo, observa que podemos plantear sus coordenadas: B(x,1,4), ya que se encuentra en la misma cara que el vértice A (que está incluida en el plano de ecuación y =1), y en la misma cara que el vértice C (que está incluida en el plano de ecuación z = 4).

Luego planteamos la igualdad entre la longitud de las diagonales:

d(A,C) = d(A,B), elevamos al cuadrado y queda:

d(A,C)² = d(A,B)², sustituimos por las expresiones en función de las coordenadas de los vértices y queda:

0² + 5² + (-5)² = (x+3)² + 0² + (-5)², cancelamos térinos y queda:

25 = (x+3)², resolvemos y tenemos dos soluciones:

a) x = -8, que no tiene sentido para nuestro problema, porque no corresponde a la abscisa de un vértice del cubo;

b) x = 2, que si corresponde a la abscisa del vértice, cuyas coordenadas son: B(2,1,4).

Luego podemos plantear el vector normal al plano como el producto vectorial:

n = AC x AB = <0,5,-5> x <5,0,-5> = <-25,-25,-25>.

Por último, con el vector normal y uno de los vértices, por ejemplo A(-3,1,9), planteamos la ecuación cartesiana implícita del plano que contiene a los vértices A, B y C:

-25(x+3) - 25(y-1) - 25(z-9) = 0, distribuimos los agrupamientos, reducimos términos semejantes y queda:

-25x -25y - 25z + 175 = 0, dividimos en todos los términos de la ecuación por -25 y llegamos a:

x + y + z - 7 = 0.

Espero haberte ayudado.

Esta integral, lo siento, es universitaria y tiene que ver con seno hiperbolico, pero te dejo un link donde podrás encontrar la solucion paso a paso...
http://www.wolframalpha.com/input/?i=int+(16%2B4t%5E2)%5E(1%2F2)

Valeria, te mandamos una "casi igual": 

(6x^2-e^x)cos(x)-(2x^3-e^x)sen(x) es por multiplicacion

Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)

Te sugiero.. Regla de la cadena
Para el b)... Derivación implicita

log₃ 9a=log₃ 9 + log₃ a = 2 + 0,8 = 2,8

Acuérdate de la propiedad: log(ab)= log a + log b

Gracias!

A mí me da esto, Nacho: