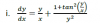-


Antonio Silvio Palmitano
el 3/11/16Vamos con una orientación.
Observa que el dominio de la función es D = R, y que es continua en todo su dominio, y además observa que la función toma valores estrictamente mayores que 1, por lo que su imagen es: I = [1,+inf)
Luego, para estudiar su crecimiento o decrecimiento, planteamos su derivada primera:
y ' = ( e^x - e^(-x) )/2 =( e^x - 1/e^x )/2 = extraemos denominador común en el agrupamiento:
= ( e^(2x) - 1 ) / 2e^x,
luego observa que el denominador es estrictamente positivo en todo el dominio, y que el numerador es estrictamente positivo para el intervalo (0,+inf), y que la derivada toma el valor 0 para x=0 (es un punto crítico, y el valor de la función para él es f(0) = 1 y corresponde a un mínimo), por lo que tenemos que la función es creciente en el intervalo [0,+inf).
Luego, planteamos para la función inversa:
y = argcoshx,
componemos con la función inversa del argumento coseno hiperbólico y queda:
coshy = x (*),
derivamos con respecto a x en ambos miembros (observa que a la izquierda debemos aplicar la regla de la cadena):
senhy*y ' = 1, sustituimos con la identidad hiperbólica senhy = V( cosh²y - 1 ) y queda.
V( cosh²y - 1 ) * y ' = 1, sustituimos con la ecuación señalada (*) y queda:
V( x² - 1 ) * y ' = 1, hacemos pasaje de factor como divisor y queda:
y ' = 1/V( x² - 1 ),
y su dominio coincide con la imagen de la función: [1,+inf).
Espero haberte ayudado.
-
No se por donde coger este sistema de ecuaciones, siempre se me queda con 0 igual a algo... Muchas gracias.



Antonio Silvio Palmitano
el 3/11/16Comencemos por multiplicar por 2 en todos los términos de la primera ecuación, y por 8 en todos los términos de la segunda ecuación, y el sistema queda:
x + 2y = 8, despejamos y queda: x = 8 - 2y (*)
8x + 2y = 29
reemplazamos la expresión (*) en la segunda ecuación y queda:
8(8 - 2y) + 2y = 29, distribuimos en el primer término a la izquierda y queda:
64 - 16y + 2y = 29, hacemos pasaje de término, reducimos términos semejantes y queda:
- 14y = - 35, hacemos pasaje de factor como divisor, resolvemos a la derecha y queda:
y = 5/2 (**).
Luego, reemplazamos en la ecuación señalada (*) y queda:
x = 8 - 2(5/2), resolvemos y queda:
x = 3.
Luego, la solución del sistema es: x = 3, y = 5/2.
Puedes verificar que la solución es válida.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 3/11/16Planteamos la sustitución: y/x = t, de donde tenemos: y = xt, y también teneoms: dy/dx = t + xdt/dx, sustituimos y queda:
t + xdt/dx = t + (1 + tan²t) / x²t², cancelamos términos y queda:
xdt/dx = (1 + tan²t) / x²t², hacemos pasajes de divisores como factores y queda:
x³t²dt = (1 + tan²t)dx, hacemos pasajes de factores como divisores buscando separar variables y queda:
t²dt/(1 + tan²t) = dx/x³, sustituimos con la identidad trigonométrica 1 + tan²t = 1/cos²t y queda:
t²cos²tdt = dx/x³.
Observa que la integral a la derecha es directa, y que su resultado es - 1/(2x²) + C.
Para la integral de la izquierda, empleamos la identidad trigonométrica: cos²t = ( 1+cos(2t) )/2, sustituyes, y podrás resolverla en forma directa en uno de los términos, y por partes en dos pasos para el segundo término.
Queda para que concluyas la tarea.
Espero haberte ayudado.
-


David
el 3/11/16(12/5)²/a² + 3²/b²=1... 144/(25a²) + 9/b²=1... (144b² + 9.25a²)/(25a²b²)=1... 144b² + 9.25a²=25a²b²..
Como a²=b²+16.... 144b² +225(b²+16)=25(b²+16)b².. 144b² +225b²+3600=25b^4 + 400b².. 25b^4 +31b² - 3600=0, que es lo mismo que obtuviste tu casi.....
Solo te faltó multiplicar por 25 a todos los miembros y pasar todo a uno de ellos...
Y ahora resuelve la ecuacion bicuadrada... Ecuacion bicuadrada -


David
el 3/11/16¿Has visto estos vídeos?... Area entre funciones 01
Para el primero te puede venir genial...
En cuanto a los demás, lo siento, pero el segundo ejercicio es de calculo universitario y unicoos, aunque a veces hago excepciones se queda en bachiller. Espero lo entiendas -
Si tengo esta ecuación logarítmica, ¿como operaría? No se que hacer con esos logaritmos que se están dividiendo.



Antonio Silvio Palmitano
el 2/11/16Como tienes un término en cada miembro de la ecuación, puedes hacer pasaje de divisor como factor y queda:
log(16-x²) = 2log(3x-4), luego aplicas la propiedad del logaritmo de una potencia y queda
log(16-x²) = log( (3x-4)², luego comparas argumentos y queda:
16 - x² = (3x - 4)², luego desarrollas el binomio elevado al cuadrado y queda:
16 - x² = 9x² - 24x + 16, luego haces pasajes de términos, reduces términos semejantes y queda:
- 10x² + 24x = 0, luego multiplicas en todos los términos de la ecuación por -1/10 y queda:
x² - (12/5)x = 0, que es una ecuación polinómica cuadrática, luego aplicas la fórmula resolvente y tienes las soluciones:
a) x = 0, que no corresponde a nuestra ecuación porque con ella no es posible calcular log(3x-4);
b) x =12/5, con la que si se pueden calcular todos los logaritmos.
Espero haberte ayudado.
-
Me podeis decir si los tengo bien
(raiz cuadrada"25+2 al cubo x3"+2 al cubo):3=5
tres multiplos del 11que esten entre el 100 y el 150
son{110,121,132}
¿es 1330 multiplo de 13?-no


Antonio Silvio Palmitano
el 2/11/16Por favor, envía foto del primer ejercicio.
El segundo está bien, has elegido tres de los cuatro múltiplos de 11 comprendidos entre 100 y 150 (el otro es 143).
La respuesta para el tercero es correcta, y si quieres justificarlo puedes descomponer en múltiplos de 13 hasta donde sea posible
1330 = 1300 + 26 + 4 =
= 13*100 + 13*2 + 4 =
= 13(100 + 2) + 4 =
= 13*102 + 4,
luego, como 1330 es la suma de un múltiplo de 13 con un número natural menor que 13,
tienes que 1330 no es múltiplo de 13.
Espero haberte ayudado.