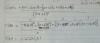-
Buen día! Me gustaría saber sí pueden ayudarme a resolver este ejercicio. Tengo un problema al momento de plantear la relación de los triángulos.


Antonio Silvio Palmitano
el 29/10/16Observa que has trazado dos triangulos rectángulos en tu gráfico:
uno (T1) con dos de sus vértices en la posición del barco y en la estación A, y otro (T2) con dos de sus vértices en la posición del barco en en la estación B, y en los dos casos tienen catetos perpendicuares a la costa.
Observa que las alturas de ambos triángulos tienen longitud 100 (en millas), y que si llamamos x a la longitud de la hipotenusa de T2,
tenemos que la longitud de la hipotenusa de T1 es (x+160).
Luego, si llamamos y a la longitud de la base del triángulo T2, tenemos que la longitud de la base del triángulo T2 es (y+200).
Luego, planteamos la relación pitagórica para ambos triángulos, y queda el sistema de ecuaciones:
(x + 160)^2 = (y+200)^2 + 100^2
x^2 = 100^2 + y^2.
Luego desarrollamos todos los binomios, resolvemos potencias y queda:
x^2 + 320x + 25600 = y^2 + 400y + 40000 + 10000
x^2 = 10000 + y^2
Luego hacemos pasajes de términos, reducimos términos semejantes y queda:
x^2 - y^2 +320x - 400y = 24400
x^2 - y^2 = 10000
Luego, sustituimos a la primera ecuación por su resta con la segunda, mantenemos la segunda ecuación y el sistema queda:
320x - 400y = 14400
x^2 - y^2 = 10000
Luego, puedes despejar de la primera ecuación y queda: x = 45 + 1,25y (*), sustituyes en la segunda ecuación y queda:
(45 + 1,25y)^2 - y^2 = 10000, desarrollas el binomio elevado al cuadrado y queda:
2025 + 112,5y + 1,5625y^2 = 10000, hacemos pasaje de término, reducimos términos semejantes, ordenamos términos y queda:
1,5625y^2 + 112,5y - 7975 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes las soluciones:
a) y = ( -112,5 - 250 )/ 3,125 < 0, que no corresponde a este problema porque y expresa una longitud y debe tomar valores estrictamente positivos;
b) y = ( -112,5 + 250 )/3,125 = 137,5/3,125 = 44 > 0, que si corresponde a este problema, luego reemplazamos en la ecuación señalada (*) y tenemos:
x = 45 + 1,25*44 = 100, que también corresponde a este problema.
Luego, ya tienes todo lo que se necesita para responder dónde se encuentra el barco.
Espero haberte ayudado.
-
Buen día!! Me gustaría saber si el procedimiento que usé para este ejercicio es correcto.
Muchas gracias!!
-


Antonio Silvio Palmitano
el 29/10/16Observa que a es raíz del numerador, por lo que puedes aplicar la regla de Ruffini:
| 1 -(a + 1) a
a | a -a
| 1 -1 | 0
Luego, tienes que el cociente queda: (x - 1), que es un factor en el numerador, que queda factorizado:
N = (x - a)(x - 1).
Observa que debes corregir el signo en un término en la factorización del divisor:
D = x^3 - a^3 = (x - a)(x^2 + ax + a^2).
Luego, planteas el cociente, simplificas y queda:
N/D = (x - 1) / (x^2 + ax + a^2), y luego pasas al límite, cuyo resultado queda: (a - 1) / (3a^2).
Espero haberte ayudado.
-
Hola buenas, resulta que tengo que hacer unos ejercicios de conjuntos para la asignatura de álgebra. Eso no lo he dado nunca en el instituto y en la clase no hemos dado nada sobre eso, los he hecho como buenamente he podido pero especialmente estos 2 no tengo ni idea. A ver si vosotros podríais ayudarme porque no tengo ni idea. Me bastaría con que me dijesen que es correcto y que no. Muchas gracias de antemano

-
Buenas tardes, estoy en primero de Económicas y os pregunto sobre elasticidad ¿me podéis decir dónde conseguir la teoría-vídeos explicativos? ya que no la encuentro. Gracias