-
Hola, como estan? me podrían ayudar con este ejercicio, necesito hacer el estudio completo de esta función
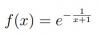


Antonio Silvio Palmitano
el 31/10/16Van orientaciones.
Observa que el dominio de la función es: D = (-inf,-1) u (-1,+inf) = R - {-1}.
Luego, planteamos sus derivadas primera y segunda, observa que debes aplicar la regla de la cadena, por lo que denominamos:
u = -1/(x+1), cuya derivadas primera y segunda quedan: u ' = 1/(x+1)² ): y u ' ' = -2/(x+1)³ ).
Luego tenemos: f(x) = e^u, cuyas derivada primera queda:
f ' (x) = e^u * u ' (*), y cuya derivada segunda queda:
f ' ' (x) = e^u * (u ' )² + e^u * u ' ' (**).
Luego planteamos la condición de punto crítico (o singular, posible máximo o posible mínimo): f ' (x) = 0, sustituimos con la ecuación señalada (*) y queda:
e^u * u ' = 0, hacemos pasaje de factor como divisor (observa que e^u toma valores estrictamente positivos), resolvemos a la derecha y queda:
u ' = 0, sustituimos la expresión u y queda:
-1(x+1) = 0, hacemos pasaje de divisor como factor, resolvemos a la derecha y queda:
-1 = 0, que es una identidad absurda, por lo que concluimos que la función no presenta puntos críticos.
Luego planteamos la condición de posible inflexión: f ' ' (x) = 0, sustituimos con la expresión señalada (**) y queda:
e^u * (u ' )^2 + e^u * u ' ' = 0, extraemos factor común y queda:
e^u * ( ( u ' )² + u ' ' ) = 0, hacemos pasaje de factor como divisor, resolvemos a la derecha y queda:
( u ' )² + u ' ' = 0, sustituimos las expresiones para las derivadas primera y segunda de u:
( 1/(x+1)²)² - 2/(x+1)³ = 0, hacemos pasaje de término y queda:
( 1/(x+1)²)² = 2/(x+1)³, resolvemos a la izquierda y queda:
1/(x+1)^4 = 2/(x+1)³, hacemos pasaje de divisor como factor, resolvemos potencias a la derecha y queda:
1 = 2(x+1), de donde puedes despejar y queda:
x = -1/2, que es un posible punto de inflexión.
Luego, queda para que estudies crecimiento y concavidad en los intervalos: (-inf,-1), (-1,-1/2),(-1/2,+inf).
Con respecto a los límites, observa que cuando x tiende a +infinito o a -infinito, tienes que el exponente tiende a 0, y por lo tanto la función tiende a 1;
pero cuando x tiende a -1 debemos plantear límites laterales:
por la izquierda, el exponente tiende a +infinito, y la función tiende a +infinito, por lo que la gráfica presenta asíntota vertical superior con ecuación x = 1,
por la derecha, el exponente tiende a - infinito, y la función tiende a 0.
Queda para que continúes la tarea.
Espero haberte ayudado.
-
Hola a todos:
En mis apuntes aparece lo siguiente:
¿Me podrían confirmar si es correcta la ecuación en caso de x1=x2? Porque en ningún ejemplo que encuentro o intento me funcionaría y=x1, ¿no sería y=y1?
Gracias de antemano.
-
AYUDA POR FAVOR
La expresión sen4x · senx es equivalente a:
Seleccione una:A.(sen4x - senx)/2
B.cos5x - cos3x
C.(cos3x - cos5x)/2
D.sen4x + senx























