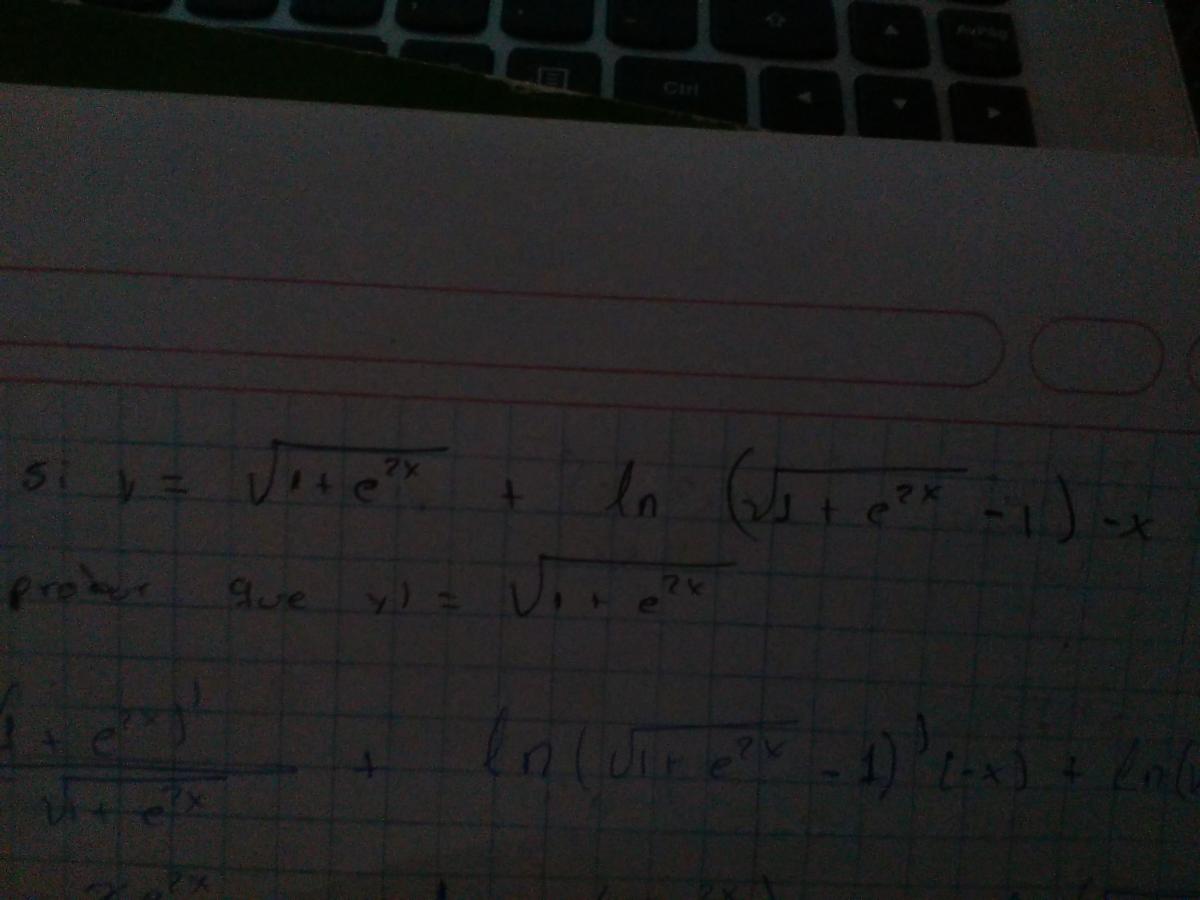Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Marcos
el 28/10/16

Hola!
Quisiera saber como resolver esta tarea pre parcial
Dadas las funciones f(x) = 3xln(2x)+4x 2 y g(x) = ax2+b , determinar los valores de a y b para que ambas funciones tengan la misma recta tangente en x = 1.
Tengo que hacer la derivada de f(x) y g(x), luego reemplazar x = 1, para despues igualar f´(x) = g´(x) y sacar cuanto vale a y b?

••0 voto/s
•
Antonius Benedictus
el 28/10/16
Así:

•1 voto/s
•

Cancelar
Paula
el 28/10/16

Necesito ayuda con este ejercicio, Antonio. Si puede ser, lo más detallado posible. Gracias de antemano. Te agradezco tu ayuda.
Expresa el 2º miembro de cada igualdad como un solo logaritmo y halla los valores de A y B
a) log A= 3log x+2log y-5log z
b) log B= 3/2 log x+ log y - 2/3 log z.

••0 voto/s
•
Antonio Silvio Palmitano
el 28/10/16
a) Puedes aplicar la propiedad del logaritmo de una potencia en cada término y queda:
logA = log(x^3) + log(y^2) - log(z^5)
Luego aplicas la propiedad del logaritmo de un producto entre los dos primeros términos y queda:
logA = log( x^3 * y^2) - log(z^5)
Luego aplicas la propiedad del logaritmo de una división y queda:
logA = log( x^3 * y^2 / z^5 ).
b) Aplicas propiedad del logaritmo de una potencia en el primer término y en el tercero y queda:
logB = log( x^(3/2) ) + logy - log ( z^(2/3) )
Luego aplicas propiedad del logaritmo de un producto entre los dos primeros términos y queda:
logB = log( x^(3/2) * y ) - log( z^(2/3) )
Luego aplicas propiedad del logaritmos de una división y queda:
logB = log( x^(3/2) * y / z^(2/3) ).
Recuerda que las propiedades de los logaritmos son:
Producto: log(ab) = loga + logb
División: log(a/b) = loga - logb
Potencia: log(a^p) = p*loga
Y recuerda que a las raíces las puedes escribir como potencias con exponentes fraccionarios:
log( (rV)(a) ) = log( a^(1/r) ) = (1/r)loga.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Víctor Miranda
el 28/10/16

En esos 5 ejercicios he intentado hacerlos, alguno los he conseguido y otros no, tengo problemas al poner la P( ) con las letras que se encuentran en el paréntesis de antes. Me ayudaría mucho que me pudiesen corregir estos ejercicios y aquello q esta mal que me lo expliquen. Gracias

••0 voto/s
•
Antonius Benedictus
el 28/10/16
Te corregimos los tres primeros:

•0 voto/s
•

Cancelar
Leo M
el 28/10/16

Una duda respecto a la unidad imaginaria de los números complejos
(-i)³= (-i)*(-i)*(-i)= -i
no se muy bien como hacer esta potencia imaginaria, esta bien el resultado?

••0 voto/s
•
Antonio Silvio Palmitano
el 28/10/16
Debes corregir el signo en tu resultado. La solución correcta es i. Debes recordar las cuatro potencias básicas de la unidad imaginaria:
i^0 = 1, i^1 = i, i^2 = -1, i^3 = -i.
Para mostrar y justificar tu resultado, puedes aplicar propiedades del producto de potencias con bases iguales:
(-i)^3 = (-1*i)^3 = distribuimos = (-1)^3 * i^3 = resolvemos el primer factor, y descomponemos el segundo:
= -1* i^2 * i = resolvemos el segundo factor = -1*(-1)*i = +1*i = i.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
xortego
el 28/10/16

Hola a todos, quisiera saber si alguno me puede decir una forma para saber si un conjunto es un espacio vectorial sin necesidad de resolver los diez axiomas, y si me pudiera dar un ejemplo, mucho mejor.
Muchas gracias a todos.

••0 voto/s
•
Antonio Silvio Palmitano
el 28/10/16
Si sabes que tienes un subconjunto de un espacio vectorial conocido, puedes hacer:
1) Demostrar que el vector nulo del espacio pertenece al subconjunto.
2) Mostrar que la suma de dos vectores del conjunto pertenece al conjunto.
3) Mostrar que el producto de un escalar por un vector del subconjunto pertenece al conjunto.
Luego, si se cumplen las tres condiciones, tienes que el subconjunto es un subespacio vectorial incluido en el espacio vectorial conocido.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Usuario eliminado
el 28/10/16

No tengo problemas para representar raíz cuadrada de dos o de cinco en la recta real, pero no sé cómo representar la raíz de once. ¿Alguien me echa una mano? O mejor, ¿alguien me muestra un dibujo?

••0 voto/s
•
Antonius Benedictus
el 28/10/16
11=9+2
9=3^2 y 2=(sqrt(2))^2
Representas un rectángulo de base "raiz de 2" (que sabes ya obtener) y altura 3.
La diagonal mide sqrt(11)

•1 voto/s
•
Usuario eliminado
el 28/10/16
Una alternativa:
11 = 36-25 = 6^2 - 5^2
Pintas la recta real, desde 0 te subes una altura 5 y desde ahí trazas un arco de circunferencia de radio 6 hacia los números positivos. El punto donde el arco corta a la recta real es sqrt(11).

•1 voto/s
•

Cancelar
Tora Kevin Yack Quispe Tapia
el 28/10/16

ln[(√1+ε^2x)-1](-x)
la derivada de esta función puedo resolverla por propiedad pero no se que hacer con el segundo miembro que queda "-ln[(√1+ε^2x)-1]"

••0 voto/s
•
Antonius Benedictus
el 28/10/16
Foto original, por favor.

•1 voto/s
•
Tora Kevin Yack Quispe Tapia
el 28/10/16

•0 voto/s
•
Antonius Benedictus
el 28/10/16
Ahora:

•1 voto/s
•

Cancelar
Tora Kevin Yack Quispe Tapia
el 28/10/16
1. como resuelvo este limite
  lim tgh(x)
  x→∞
••0 voto/s
•
Antonius Benedictus
el 28/10/16
Así, Tora:

•1 voto/s
•
Tora Kevin Yack Quispe Tapia
el 28/10/16
disculpa no entiendo la ultima el limite es -1 pero mas arriba dice 1 por favor

•0 voto/s
•
Antonius Benedictus
el 28/10/16
Te hice dos límites: para x tiende a +infinito y para x tiende a -infinito.

•0 voto/s
•

Cancelar
Alex Grattan
el 28/10/16

No se como hacer esta integral , necesito ayuda plis

••0 voto/s
•
David
el 28/10/16
Puedes hacerla por cambio de variable.... t²=x...... 2t.dt=dx.... Y te quedará... ∫ [(1/(e^√x . √x)]dx = ∫ [(1/(e^√t² . √t²)] 2t.dt = ∫ [2t.dt/(e^t . t) = 2 ∫ dt/e^t = 2 ∫ e^(-t). dt =
-2.e^(-t) = -2 / e^t = -2/e^√x

Te sugiero... Integrales por cambio de variable

•0 voto/s
•

Cancelar