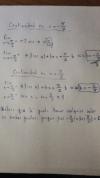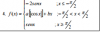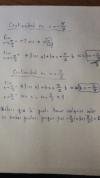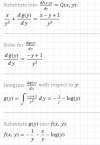Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

wilder fernendez
el 28/10/16

^{como se deriva de un valor absoluto}

••0 voto/s
•
Antonio Silvio Palmitano
el 28/10/16
Debes expresar como función a trozos. Va un ejemplo:
f(x) = | x - 4 |, de acuerdo con la definición de valor absoluto, la expresión de la función queda:
f(x) =
x - 4 si x - 4 >= 0, de donde queda: x >= 4
-(x - 4) si x - 4 < 0, de donde queda: x < 4.
Luego, distribuimos en la expresión del segundo trozo y queda:
f(x) =
x - 4 si x >= 4
- x + 4 si x < 4.
Luego, la expresión de la derivada queda:
f ' (x) =
1 si x > 4
no está definida si x = 4 (*)
-1 si x < 4
Para el caso del punto de corte x = 4 vemos que la función derivada no está definida (*), y lo puedes verificar porque las derivadas laterales no coinciden, y también se puede corroborar planteando las derivadas laterales empleando la definición.
Y en otros ejercicios, donde no sea tan evidente si está o no definida la función derivada en el punto de corte, se deben calcular las derivadas laterales con la definición.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Sofía Loncón
el 28/10/16

Hola, disculpen, tengo que resolver esto y no sé cómo hacerlo:

1. Determine si la siguiente proposición es verdadera o falsa. Demuestre en caso que sea verdadera y de un contraejemplo o justifique adecuadamente en otro caso.

Dadas las funciones, α : A ⊆ R → R, β : B ⊆ R → R, se define la función compuesta β ◦ α : C ⊆ R → R y x |→ β( α(x) ) donde C es distinto de vacío y corresponde al dominio natural de definición de la función compuesta. Entonces, se cumple que el dominio natural de continuidad de la función compuesta β ◦ α es igual a C.

Gracias!!

••0 voto/s
•
David
el 28/10/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Feli Gariboldi
el 27/10/16
hola, disculpen que no les detalle mi procedimiento es que en realidad no se ni como empesar.
el ejercicio es el siguiente: Hallar Base y dimensión de S∩T
tal que:
- S={(x,y,z) ∈ R³ / x - y + 2z = 0},
- T={gen{(0,-3,0),(1,1,1)}
Si me dicen como hacerlo se los agradecería mucho.
••0 voto/s
•
Antonio Silvio Palmitano
el 28/10/16
Puedes comenzar planteando la combinación lineal para un vector genérico del subespacio T:
<x,y,z> = a<0,-3,0> + b<1,1,1> = <b,-3a+b,b>
luego planteamos el sistema de ecuaciones:
x=b, sustituimos en las otras dos ecuaciones:
y=-3a+b, queda: y = -3a + x (observa que a no figura en las otras ecuaciones, por lo que interpretamos puede tomar cualquier valor real)
z=b, queda z = x, que es la condición que cumplen las componentes de los vectores del subespacio T.
Luego, los vectores del subespacio S intersección T cumplen las condiciones de ambos subespacios que son:
x = z (*)
x - y + 2z = 0, sustituimos la expresión dela primera ecuación y queda: z - y + 2z = 0, de donde tienes 3z = y (**).
Luego planteamos el vector genérico del subespacio intersección entre S y T:
u = < x , y , z > = sustituimos a partir de las ecuaciones señaladas = < z , 3z , z > = z< 1,3,1>.
Luego, una base del subespacio S intersección T es: B = { <1,3,1> }, y su dimensión es 1.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Alex Domínguez
el 27/10/16

Hola, mi pregunta es como diagonalizar la siguiente matriz por medio de a=PxD(matriz diagonal ( lambda ))xP^-1 , enviaría mi intento pero está enrevesadísimo, la matriz es
A = ( 0,1,1 / 1,0,1 / -1,1,0 ) por filas expresada
Gracias !

••0 voto/s
•
David
el 28/10/16
Echale un vistazo.. ALGEBRA Matriz Diagonal
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?

•0 voto/s
•

Cancelar
Alicia Quesada Cabrera
el 27/10/16

Como se calcula la continuidad de una función cuando esta tiene incognitas(a,b)

••0 voto/s
•
Ángel
el 27/10/16
Mira el ejercicio de "DueFreitas" (2 mensajes más abajo), esta es la solución...

primero se calcula el límite por un lado y obtenemos el valor numérico, y al otro lado tendremos un valor multiplicando (o sumando o restando o dividiendo) a nuesta incognita "a" o "b"...y obtenemos "a "y/o "b" en función del valor numérico
Así repetiremos con cada posible punto de discontinuidad....ni que decir tiene que la función seno y coseno son continuas y excepto esos puntos que estudiaremos con los límites, toda la función es contínua (valga la redundancia)

•0 voto/s
•

Cancelar
Alex Rubiano
el 27/10/16

Como se obtiene el rango de una matriz por Gauss?

••0 voto/s
•
ubildo
el 27/10/16
Para calcular el rango de una matriz por el método de Gauss:
Calculamos el rango por filas. Si la matriz tuviese más filas que columnas, podemos usar su traspuesta, recordemos que
Mediante transformaciones elementales, hacemos ceros todos los elementos por debajo de la diagonal principal.

El rango es el número de filas (sin contar las filas nulas)
Ejemplo
Calculamos el rango de la matriz $A = \left( \begin{array}{cccc} 1 & 1 & 0 & 1 \\ 1 & 0 & -1 & 1 \\ 2 & 1 & -1 & 2 \end{array} \right)$
Para hacer los dos primeros ceros de la primera columna, hacemos las siguientes transformaciones de filas:
$F_1 - F_2 \longrightarrow F_2$
$2 \cdot F_1 - F_3 \longrightarrow F_3$
Quedando la matriz así: $A = \left( \begin{array}{cccc} 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \end{array} \right)$
Para el último cero restamos las filas 2 y 3: $F_2 - F_3 \longrightarrow F_3$
$A = \left( \begin{array}{cccc} 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right)$
El rango es el número de filas no nulas, por tanto

•0 voto/s
•

Cancelar
DueFreitas
el 27/10/16

Profe como resuelvo esto por limites ? nose como trabajar las funcion Partes.

••0 voto/s
•
Ángel
el 27/10/16

•0 voto/s
•

Cancelar
Mónica Álvarez
el 27/10/16

Hola ¿ Alguien me puede ayudar con este problema ? Sólo se me ocurre por la cuenta de la vieja y veo varios resultados posibles
El número de participantes en un desfile es tal que pueden desfilar formados de 3 en 3, de 5 en 5 o de 25 en 25, pero no pueden hacerlo de 4 en 4 ni de 9 en 9. ¿Cuál es el número de participantes si sabemos que es mayor que 1000 pero menor que 1250

••0 voto/s
•
Antonio Silvio Palmitano
el 27/10/16
Llamemos N al número buscado
Observa que debe se múltiplo de 3, porque marchan de 3 en tres.
Observa que debe ser múltiplo de 5, porque marchan de 5 en cinco.
Observa que debe ser múltiplo de 25, porque marchan de 25 en veinticinco.
Por lo tanto, para satisfacer las tres condiciones, tenemos que N debe ser múltiplo de 3*25 = 75.
Pero observa también que no puede ser múltiplo de 4 (no pueden marchar de 4 en cuatro), ni puede ser múltiplo de 9 (no pueden marchar de 9 en nueve).
Luego, es cuestión de investigar cuál o cuáles múltiplos de 75 están comprendidos entre 1000 y 1250.
Algunos múltiplos de 75 son:
... - 900 - 975 - 1050 - 1125 - 1200 - 1275 - 1350 - ...
Observa que debemos descartar a 1125 porque es múltiplo de 9, y también a 1200 porque es múltiplo de 4, por lo tanto la solución es: N = 1050.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Thaly
el 27/10/16

alguien me puede ayudar con esta ec.diferencial
y'=y/(x-y+1)

••0 voto/s
•
Antonius Benedictus
el 27/10/16
1º:

•0 voto/s
•
Antonius Benedictus
el 27/10/16
2º

•0 voto/s
•
Antonius Benedictus
el 27/10/16
3º

•0 voto/s
•
Antonius Benedictus
el 27/10/16
4º

•0 voto/s
•

Cancelar
ubildo
el 27/10/16

hola tengo una duda en una ecuacion de 2do grado con bascara me da resultadosal verificar si son raices los resultados son de 0.14......... y 0.8 mi duda es eso es raiz si es cero con coma
muchas gracias

••0 voto/s
•
David
el 28/10/16
Lo siento, no entiendo...

•0 voto/s
•

Cancelar