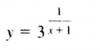-
Hola, buenas noches, me podrían ayudarme con estos 2 problemas de análisis matemático 2 por favor? En el problema 8 mi duda es como conseguir el punto que me piden, si solo tengo una ecuación( distancia punto-recta) y 3 incógnitas (x,y,z), y el problema 10 no se como hacerlo. Gracias de antemano.


Antonio Silvio Palmitano
el 26/10/16Van orientaciones para que puedas intentar resolver los ejercicios. Designamos P(x,y,z) al punto cuyas coordenadas debemos calcular.
8) Como sabemos que el punto pertenece a la recta, podemos plantear dos ecuaciones a partir de las ecuaciones cartesianas simétricas del enunciado (observa que igualamos al primer miembro de la doble desigualdad con el tercero, y al segundo con el tercero):
(x-3)/2 = z, de donde podemos despejar: x = 2z + 3 (*).
-y/2 = z, de donde podemos despejar: y = -2z (**).
Luego, como tenemos que la distancia entre el punto P y el punto O(0,0,0) es igual a V(13), planteamos (observa que empleamos la expresión para calcular la distancia entre dos puntos):
V( (x-0)^2: + (y-0)^2 + (z-0)^2 ) = V(13), cancelamos raíces y términos nulos en los agrupamientos y queda:
x^2 + y^2 + z^2 = 13 (***).
Ahora queda para que sustituyas las expresiones señaladas (*) (**) en la ecuación señalada (***), y verás que llegarás a dos puntos que conforman el conjunto solución.
10) Planteamos las ecuaciones cartesianas simétricas de la recta (la llamamos L) que buscamos:
(x-3)/a = (y+3)/b = (z+5)/c, donde a, b, c son las componentes del vector director, de las que debemos determinar sus valores.
Luego, observa que podemos proceder en forma similar a la que empleamos en el ejercicio anterior:
igualamos el primer miembro con el tercero, operamos y queda la ecuación: cx - 3c = az + 5a (*),
igualamos el segundo con el tercero, operamos y queda la ecuación: cy + 3c = bz + 5b (**).
Luego, hacemos lo propio con las ecuaciones cartesianas simétricas de las rectas cuyas ecuaciones tenemos en el enunciado (las llamamos L1 y L2):
para L1 tenemos:
-3x + 3 = 5z + 5, operamos y queda: 3x + 5z = -2 (***),
-3y + 6 = -2z - 2, operamos y queda: 3y - 2z = 8 (****);
para L2 tenemos:
2x - 4 = z + 3, operamos y queda: 2x - z = 7 (*****)
2y + 2 = -3z -9, operamos y queda: 2y + 3z = -11 (******).
Luego planteamos la intersección entre la recta L y la recta L1, y nos queda el sistema con las ecuaciones señaladas (*) (**) (***) (****):
cx - 3c = az + 5a
cy + 3c = bz + 5b
3x + 5z = -2
3y - 2z = 8
observa que tenemos cuatro ecuaciones y seis incógnitas, por lo que despejamos x, y, z con tres de las ecuaciones y sustituimos sus expresiones en la cuarta ecuación (que quedará con incógnitas: a, b, c) (+);
luego planteamos la intersección entre L y L2, y nos queda el sistema con las ecuaciones señaladas (*) (**) (*****) (******):
cx - 3c = az + 5a
cy + 3c = bz + 5b
2x - z = 7
2y + 3z = -11
observa que tenemos cuatro ecuaciones y seis incógnitas, por lo que despejamos x, y, z con tres de las ecuaciones y sustituimos sus expresiones en la cuarta ecuación (que quedará con incógnitas: a, b, c) (++), y observa también que debemos plantear las intersecciones por separado, porque los puntos de intersección entre L y L1, y entre L y L2 pueden ser distintos.
Luego, queda para que hagas la tarea, y llegarás a un sistema con las ecuaciones que obtengas al resolver el primer sistema (+) y el segundo (++), verás que podrás llegar a la expresión general del vector director de la recta L.
Haz el intento, y si es preciso puedes volver a consultar.
Espero haberte ayudado.
-


David
el 26/10/16En el intervalo (1,e²) la funcion f(x)=x+lnx... Si quieres demostrar que existe un punto en el cual f(x1)=π/2 debes demostrar que x+lnx=π/2... x+lnx-π/2=0.
Para ello debes recurrir al Teorema de Bolzano. Teorema de BOLZANOLo mismo para f(x2)=3π/2
En el 2º, lo primero es hallar fog(x) para el intervalo que te dan. En ese intervalo, f(x)=x+lnx y g(x)=senx/x...
Por tanto gof(x)= sen(x+lnx) / (x+lnx). Y de nuevo, Bolzano.. . Tendrás que demostrar, por supuesto que f(x) y gof(x) y g(x) son continuas en el intervalo (1,e²).
Para ello halla el dominio de esas funciones... Dominio de una funcionP.D. Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
-
hola chicos unicoos,podrian ayudarme con este problema, de antemano gracias :)
encontrar todos los elementos de la parabola(vertice, foco, directriz , ecuacion de la directriz, y lado recto)con eje paralelo al eje de las x y pasa por los puntos a(3,3) , b(6,5) y c(6,-3)


Antonio Silvio Palmitano
el 26/10/16Vamos con una orientación.
Si es una parábola con eje de simetría paralelo al eje OX, puedes plantear como ecuación cartesiana explícita:
x = ay^2 + by + c, en la que a, b, c son números reales a determinar.
Luego, como los puntos pertenecen a la parábola, puedes reemplazar sus coordenadas y quedan tres ecuaciones:
3 = 9a + 3b + c (para el punto A(3,3))
36 = 25a + 5b + c (para el punto B(6,5))
6 = 9a - 3b + c (para el punto C(6,-3).
Luego, deberás resolver el sistema de ecuaciones (puedes emplear el método de sustitución u otro que hayas visto en clase):
9a + 3b + c = 3
25a + 5b + c = 36
9a - 3b + c = 6
Luego, tendrás que completar binomio elevado al cuadrado para y, y obtendrás la ecuación canónica (seguramente has visto el procedimiento en clase), y a partir de ella podrás resolver todo lo que te piden en el enunciado.
Haz el intento, y si te es preciso, puedes volver a consultar.
Espero haberte ayudado.
-
Buenas noches, llevo atascado en esto ejercicio un buen rato. A ver si alguien me puede ayudar a encontrar la función inversa. Muchas gracias.


Antonio Silvio Palmitano
el 26/10/16Según se entiende de tu enunciado, la expresión 1/(x+1) es exponente, y la base de la potencia es 3.
Observa que el dominio de la función es: D = R - {-1}.
Puedes tomar logaritmos en ambos miembros:
lny = ln( 3^( 1/(x+1) ), aplicamos propiedad del logaritmo de una potencia a la derecha y queda:
lny = 1/(x+1) * ln3, permutamos las variables (recuerda que estamos buscando la expresión de la función inversa):
lnx = ln3 * 1/(y+1), hacemos pasaje de divisor como factor:
lnx * (y+1) = ln3, hacemos pasaje de factor como divisor:
y + 1 = ln3/lnx, hacemos pasaje de término y queda:
y = ln3/lnx - 1, que es la expresión de la función inversa y observa que su dominio es: Di= (0,1) u (1,+inf).
Espero haberte ayudado.
-
hola alguien me puede ayudar con esta integral ∫ x^3/(1+x^2) dx
-
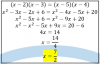
Buenas, me encuentro con álgebra y no supe resolver el siguiente problema:
hallar un sistema de números directores para cualquiera de las rectas perpendiculares a los lados del triangulo cuyos vértices son: (-5; 1; 2) ; (3; 0; 2) ; (1; -8; 9) .
La respuesta es: [7 ; 56 ; 58]
Espero me puedan dar una mano!