-
ejercicio selectividad
resuelve la ecuacion matricial (e) X·C + X·D - X·E = I ; seria asi? X(C+D-E) : X=-C-D+E : No se si lo estoy haciendo bien gracias
-
hola chicos unicoos!! tengo una PEQUEÑILLA duda .Me Explico la ecuacion matricial C.X+D=E al despejar x C´.CX=E-D: LUEGO ME QUEDA X=C`(E-D) hago primero la resta dentro del parentesis o hago primero la multiplicacion? no se si me e explicado gracias..
-
Hola, alguien puede ayudarme con esta ecuación?
P∧1/2 = 125/P
GRACIAS!


Antonio Silvio Palmitano
el 25/10/16Si la ecuación es:
P^(1/2) = 125 / P, haces pasaje de divisor como factor:
P^(1/2) * P = 125, aplicas propiedad del producto de potencias con bases iguales a la izquierda:
P^(1/2 + 1) = 125, resuelves el exponente a la izquierda, y factorizas a la derecha:
P^(3/2) = 5^3, expresas la potencia con exponente fraccionario como potencia cuya base es una raíz:
( V(P) )^3 = 5^3, cancelamos exponentes (observa que tienes una igualdad entre cubos):
V(P) = 5, haces pasaje de raíz como potencia:
P = 5^2, resuelves a la derecha:
P = 25.
Puedes verificar que la solución es correcta reemplazando en la ecuación inicial.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 25/10/16Primero establezcamos las condiciones que cumplen los elementos x que pertenecen al dominio (D) de la función.
Observa que el denominador en el argumento del logaritmos se anula para x = - 1 y para x = 1, por lo que estos dos valores no pertenecen al dominio de la función.
Luego, observa que el numerador (N) de dicha expresión puede factorizarse y queda: N = (x+1)(x+2).
Luego, observa que el denominador de dicha expresión puede factorizarse y queda: D = (x+1)(x-1).
Luego, el argumento del logaritmo queda, luego de simplificar: N/D = (x+2)/(x-1).
Por último, observemos que el argumento del logaritmo debe ser estrictamente positivo, por lo que tenemos dos opciones:
a) x+2 > 0 y x-1> 0, que nos conduce al subintervalo: (1,+inf);
b) x+2 < 0 y x-1 < 0, que nos conduce al subintervalo: (-inf,-2).
Luego, el dominio de la función queda: D = (-inf,-2) u (1,+inf).
Luego, a fin de facilitar los cálculos, puedes aplicar la propiedad del logaritmo de un cociente:
ln(N/D) = ln|N| - ln|D| (observa que los argumentos de los logaritmos los escribimos como valores absolutos), y para la expresión de la función nos queda:
f(x) = ln|x+2| - ln|x-1|, luego, su derivada primera queda:
f ' (x) = 1/(x+2) - 1/(x-1) (observa que los denominadores los escribimos sin valor absoluto), y la derivada segunda queda:
f ' ' (x) = -1/(x+2)^2 + 1/(x-1)^2.
Luego, queda para que analices la existencia de puntos críticos (o singulares) con la condición f ' (x) = 0,
para luego pasar al análisis de los intervalos de crecimiento o decrecimiento,
y la existencia de posibles inflexiones con la condición f ' ' (x) = 0,
para luego pasar al análisis de los intervalos de concavidad o convexidad.
Haz el intento de terminar la tarea y, si te es preciso, puedes volver a consultar.
Espero haberte ayudado.
-


David
el 25/10/16X=A^(-1).B... Obten la inversa de la matriz A. Multiplica la matriz obtenida por B...
Matrices Ecuaciones matriciales Matriz inversa, adjunta y traspuesta Operaciones con matrices
Te sugiero... -
hola buenos dias!!!! tengo una duda con la factorizacion de polinomios, para factorizar x^3+8, me dice que es (x+2)(x^2-2x+4) y no entiendo como se llega hasta ahi!! gracias si alguien me lo puede explicar!!


David
el 25/10/16¿has visto este vídeo?.... Se trata de hacer Ruffini con x=-2... Factorizacion de polinomios 02
-
-
Hola Unicos, me podrian ayudar con el siguiente sistema de ecuaciones
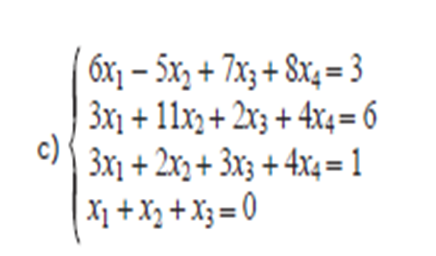


Facundo
el 25/10/16Hola Leonardo, te dejo la resolución del sistema, que es un SI, un sistema incompatible, y luego un vídeo para la resolución por gauss
Metodo: https://www.youtube.com/watch?v=31TZU8vjN0U
Saludos!