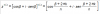-
Calcular la integral indefinida y verificar su resultado por derivación ∫45dx/√2x^2-1 ∫kF(x)dx=k∫f(x)dx ∫f(g(x)).g'(x)dx=∫f(u)du, u=g(x)
Me pueden ayudar indicando si estoy bien con las fórmulas a utilizar


David
el 26/10/16La primera es cortrecta... ∫45dx/√(2x²-1) = 45 ∫dx/√(2x²-1) Pero despues la formula que indicas no es correcta...
Deberás integrar ∫dx/√(2x²-1) ,que no es nada sencilla y tiene que ver con coseno hiperbolico..
¿Es posible que te hayas confundido al copiar el enunciado y te hallas comido una x en el numerador?
No puedo ayudarte mucho más pues la integral que te ha quedado es universitaria... Unicoos, por ahora se queda en bachiller... -
Hola Unicoos, quería confirmar una duda que tengo, en esta ecuación logarítmica, (lo subrayado en rojo) se supone que como está restando según las propiedades de los logaritmos una resta se convierte en división, pero en este caso como me lo pone entre paréntesis es lo que indica en el paréntesis verdad?
Muchas gracias.
-
Alguien puede ayudarme y resolverme esta derivada?
y= e^x + e^-x
------------------
2


Antonio Silvio Palmitano
el 25/10/16Observa que puedes distribuir el denominador y la expresión queda:
y = (1/2)e^x + (1/2)e^(-x), luego puedes derivar término a término (directo en el primer término, y con regla de la cadena en el segundo):
y ' = (1/2)e^x + (1/2)e^(-x) * (-1), luego resuelves factores numéricos en el segundo término y queda:
y ' = (1/2)e^x - (1/2)e^(-x), luego tomas denominador común y queda:
y ' = ( e^x - e^(-x) ) / 2.
Espero haberte ayudado.
-
Hola Unicoos, en este sistema de ecuaciones logarítmicas, puedo despejar la (x)de dos formas distintas (lo rodeado en naranja) pero una (x) me da resultado positivo y negativo y la otra solo resultado positivo, con cual me quedo?



Antonio Silvio Palmitano
el 25/10/16La segunda forma es la correcta.
Observa también que x e y son argumentos de logaritmos, por lo que tenemos que deben ser estrictamente positivos: x > 0 e y > 0.
Observa la tercera línea de tu primera columna de trabajo, tienes:
log(x^2) = 6, compones con la función inversa del logaritmo en base 10 en ambos miembros y queda:
x^2 = 10^6, luego haces pasaje de potencia como raíz:
x = V(10^6), luego simplificas índice de raíz con exponente de potencia y queda:
x = 10^3, resuelves y queda:
x = 1000.
De las dos posibles soluciones que encontraste en tu desarrollo debes descartar x = -1000 porque no corresponde a nuestro problema, por no ser estrictamente positiva.
Espero haberte ayudado.
-
Hola mi gran duda sobre estos dos verdaderos/falsos:
- Si y = f(x) es una funcion de x, entonces y es decreciente en x si ocurre que f´(x) < 0
- Si f y g son funciones continuas en un intervalo cerrado [a, b] y derivables en (a, b) y ademas, es f´(x) = g´(x) para todo x ∈ (a, b), entonces f y g difieren en una constante, es decir, existe k ∈ R tal que f(x) = g(x) + k para todo x ∈ [a, b]
Saludos!
-
Mi duda es en Estadistica y probabilidad.
Ejercicio:
Las siguientes probabilidades fueron obtenidas de los registros dela policia, referidos a los accidentes de transito ocurridos por no utilizar cinturon de seguridad.
Datos:
*El 6% de las personas llevan puesto el cinturón de seguridad y sufren heridas graves
*El 60% de las personas utilizan el cinturón de seguridad.
*De las personas que no utilizan el cinturón de seguridad, el 40% no sufre heridas graves.
*El 20% de los conductores que utilizan el cinturon de seguridad y sufren heridas graves, se salvaron.
*el 65% de los conductores que no utilizan cinturon de seguridad y sufrieron heridas graves, no se salvaron.
Determinar:
a) Si la persona se saalvó, ¿Cuál es la probabilidad de que sufrieran heridas graves y no llevara puesto el cinturon de seguridad?
b) Cuál es la probabilidad de una persna no sufra heridasa graves ó llevara puesto el cinturón?
/Tengo dudas de sobre como realizar este ejercicio, por la cantidad de información, si alguien me puede ayudar a resolverlo sería genial n,n_ Gracias.


David
el 26/10/16Debes construir un arbol de probabilidad, como en estos vídeos... Probabilidad total - Diagrama de Arbol
P(cinturon)=0,6........... P(heridas graves/C)=0,06...............................P(salvarse)=0,2
.....................................................................................................................P(no salvarse)=0,8
........................................P(no heridas graves/C)=0,94
P(no cinturon)=0,4......P(heridas graves/no cinturon)=0,6...............P(salvarse)=0,35
.....................................................................................................................P(no salvarse)=0,65........................................P(no heridas graves/no cinturon)=0,4
a) 0,4. 0,6 .0,35
b) La probabilidad de no sufrir heridas graves es 0,6.0,94 + 0,4.0,4=0.564 + 0.16=0.724
P(NH U C)= P(NH) + P(C) - P(NH ∩ C) = 0.724 + 0,6 - 0,6.0,94
-
Hola Unicoos,
No entiendo en estos logaritmos, por qué mi profesora lo pone como en el recuadro naranja , no sé de donde saca log en base 5 de 5² supongo que es para tachar los logaritmos y poder resolver la x. Yo lo hago como en la derecha, cuando se hace el método de la izquierda y cuando el de la derecha? Y me podríais explicar de donde sale esa igualación de logaritmos a cada lado de la igualdad en el recuadro naranja y para qué sirve, no lo entiendo muy bien.

Muchas gracias