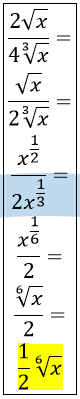-
Alan Mora
el 20/10/16Buen día unicoos, ayer tuve un examen de mate, y me quedé con una duda, lim x -->5 = x^2+4x-k/(√x-5) (claro que el denominador es la raíz de (x-5), no la raíz de (x) - 5), ¿Cuánto tiene que valer K para que ese límite de 14? llegué a la conclusión de que tenia que valer -45 pero no me convenció del todo por que el ejercicio lo dejé a medias, y aplicando los métodos que me enseñaron caía siempre en indeterminación, o resultado infinito, siendo que tenia que buscar una forma para que ese límite de 14 sí o sí. Muchas gracias profes y unicoos!
-
Alejandro Ballesteros
el 20/10/16
Hola podrían resolver estos ejercicios? Muchas gracias
Facundo
el 20/10/16Hola Alejandro, son muchos ejercicios y creo que puedes encontrar información en cualquier sitio.
Para el ejercicio 1)Matriz inversa - https://www.youtube.com/watch?v=3BpGef99HEs
- https://www.youtube.com/watch?v=nHEFxcJ-QPM
Para el ejercicio 2) - https://www.youtube.com/watch?v=ub2Y0Cvz-yE
Para el 3) Al final de la pagina dice "mas propiedades" las que tienes que usar están ahí
- http://recursostic.educacion.es/descartes/web/materiales_didacticos/determinantes_api/propiedades_de_los_determinantes.htm
Para el 4) - https://www.youtube.com/watch?v=TBAwZjxyGbU
Para el 5) - https://www.youtube.com/watch?v=bx-vGQFRXlo
Saludos!
Alejandro Ballesteros
el 20/10/16
Alejandro Ballesteros
el 20/10/16
Facundo
el 20/10/16
Alejandro Ballesteros
el 22/10/16 -
Raisa
el 20/10/16Hola veras tengo una duda. Estoy en primero de bachillerato y me pide racionalizar 3 raíz de 2 partido de 3 mas raíz de 2 . Podríais resolvérmelo?Y después otro que es 3 raíz de 5 menos 2 raíz de 2 partido de 2 raíz de 5 mas 3 raíz de 2 . Muchas gracias lo tengo que entregar para mañana y es urgente
David
el 20/10/163√2 / (3+√2) si multiplicas a numerador y denominador por 3-√2 te quedará... 3√2(3-√2) / ((3+√2) (3-√2)) Aplicando identidades notables en el denominador...
3√2(3-√2) / (3²-√2²) = 3√2(3-√2) / (9-2) =3√2(3-√2) / 7.. Aplicando distributiva en el numerador... (9√2-3√2√2) / 7 = (9√2-3.2) / 7 = (9√2-6) / 7
De verdad, de corazón, te sugiero que veas detenidamente el vídeo que te recomendé.... Está duda es de 2º-3º ESO.... Y te tocará repasar radicales si sigues sin entenderlo. Besos!
(3√5 -2√2) / (2√5+3√2) = (3√5 -2√2)(2√5-3√2) / ((2√5+3√2)(2√5-3√2)) = (6√25-9√10-4√10+6√4) / (2²√5²-3²√2²) = (6.5-13√10+6.2) / (4.5-9.2) =
= (30-13√10+12) / (20-18) = (42-13√10) / 2 = 21 - (13/2)Raisa
el 20/10/16Muchas gracias David una ultima duda el enunciado es este Utiliza los exponentes fraccionarios para simplificar las siguientes expresiones y sacar factores siempre que sea posible fuera del signo radical y tengo 2 por raíz de x partido de 4 raíz de x elevada a la 3. Como se haria? Un saludo
Antonio Silvio Palmitano
el 20/10/16Recuerda que una raíz cuyo argumento es una potencia (o una potencia cuyo argumento es una raíz) puede escribirse como una potencia del argumento, con exponente fraccionario, en el que el numerador es el exponente de la potencia, y el denominador es el índice de la raiz.
En tu ejercicio tienes una división:
el numerador (N) es: N = 2V(x) = 2V(x^1) = 2x^(1/2);
el denominador (D) es: D = 4V(x^3) = 4V(x^2 * x^1) = 4V(x^2)V(x^1) = 4xV(x) = 4x*x^(1/2).
Luego tienes la expresión fraccionaria:
N/D = 2x^(1/2) / ( 4x*x^(1/2) ) = simplificamos factores racionales:
= 1/(2x) = 1 / (2x^1) = expresamos la potencia del denominador en el numerador, pero cambiada de signo:
= 1x^(-1) / 2 = (1/2)x^(-1).
Espero haberte ayudado.
Raisa
el 20/10/16 -
Fermat
el 20/10/16En este ejercicio me piden estudiar el sistema según los valores de los parámetros α y β y resolverlo cuando sea compatible. No me sale! , ayuda
-
Ángel López González
el 20/10/16 -
Carlos Ojeda
el 20/10/16Hola, hallo bien este dominio? Gracias
Antonio Silvio Palmitano
el 20/10/16La primera condición la has planteado correctamente:
V(2 - x) + V(x - 1) distinto de 0.
Luego, debes observar que los argumentos de las raíces deben ser mayores o iguales a cero (pero no simultáneamente iguales a 0, porque no se cumpliría la primera condición), por lo tanto tenemos:
2 - x >= 0, en la que hacemos pasaje de término y queda: 2 > = x, la que leída de derecha a izquierda queda: x <= 2 (*);
x - 1 > = 0, en la que hacemos pasaje de término y queda: x >= 1 (**):
y observa que para que el denominador se anule debería ocurrir que x sea igual a 1 e igual a 2 a la vez, por lo que ésto no puede ocurrir nunca.
Por lo tanto, por las condiciones señaladas en las inecuaciones (*) (**), tenemos que el dominio de la función es el intervalo: [ 1 , 2 ].
Espero haberte ayudado.
-
Leonardo Ariel Meza
el 20/10/16Hola no logro entender como se hace esto. Alguien e podría ayudar?
Antonio Silvio Palmitano
el 20/10/16La ecuación general de la familia de superficies de nivel para una función de tres variables es:
f(x,y,z) = k, donde k es un nùmero real.
a) La ecuaciòn general de la familia de superficies de nivel es:
V(x -y) - lnx = k (*),
luego, para determinar cuàl es la ecuaciòn de la superficie de nivel que pasa por el punto de coordenadas Po(3,-1,1), reemplazamos sus coordenadas en la ecuación señalada (*) y qeuda:
V(3 - (-1)) - ln3 = k, resolvemos en el argumento de la raìz cuadrada y queda:
V(4) - ln3 = k, resolvemos el primer tèrmino y queda:
2 - ln3 = k, luego reemplazamos el valor de k que hemos hallado en la ecuación señalada (*) y queda:
V(x -y) - lnx = 2 - ln3, que es la ecuación de la superficie de nivel de la función f que pasa por el punto Po.
Haz el intento con los demás ejercicios y, si te es necesario, puedes volver a consultar.
Espero haberte ayudado.
-
miky
el 20/10/16Amigos por favor me ayudarían con estos dos ejercicios
-
Facundo
el 20/10/16Hola a todos, me darian una mano con este ejercicio? quisiera saber si lo resolvi bien, porque mi profesor lo hizo con una matriz de cambio de base. El resultado es el mismo, pero esta bien el metodo que utlice o no siempre se puede hacer?
Muchas gracias!!
