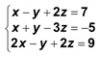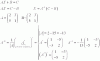-


Antonio Silvio Palmitano
el 20/10/16Si el ejercicio consiste en expresar con una única raíz y con denominador racionalizado, observa que:
en el denominador, que al final de tu primera línea quedó (indicamos raíz sexta como (6V)):
(6V)( 2^12 * x^24 ) = distribuimos la raíz = (6V)(2^12) * (6V)(x^24) = simplificamos índices de raíces con exponentes de potencias = 2^2 * x^4.
Por lo tanto, la expresión final con denominador racionalizado queda (indicamos raíz octava como (8V)):
(8V)(2^3) / (2^2 * x^4).
Espero haberte ayudado.
-
Holaa, he estado resolviendo este ejercicio en donde tengo que determinar el ángulo que se forma entre el vector a y el b. El problema es que el resultado que supuestamente me tiene que dar es 55,2 ° y bueno, no me da..
a= (3i + 5j + 7k)
b= (8i - 6j - 2k)
-
Alguien puede ayudarme a resolver este prooblema? Llevo un tiempo pensándolo y no se me ocurre como hacerlo.
Tenemos un cuadrado de lados de 10m. Desde un borde de este hay una cuerda de 15m atada a un perro. En que area podrá moverse el perro?


Antonio Silvio Palmitano
el 20/10/16Observa en la fotografía (disculpa que el dibujo esté hecho a mano alzada): hemos ubicado en uno de los lados del cuadrado, a una distancia x (menor que 5) de uno de sus vértices, el punto de amarre de la soga, y observa que con su longitud nos quedan determinados cuatro sectores: un semicírculo, y tres cuartos de círculo, que juntos conforman el área total en la que podría desplazarse el perro del problema. Observa también que la distancia x debe estar comprendida entre 0 y 10 metros. Observa también que la expresión final corresponde a una función de x, a la que denominamos A(x), cuyo dominio es el intervalo cerrado [0,10].
Espero haberte ayudado.
-
Buenas noches, ¿me pueden ayudar con este ejercicio?
Encuentra el polinomio P(x) de segundo grado cuyas raíces sean 1 y -2 y tal que P(3)=30.
Gracias.
-


Antonio Silvio Palmitano
el 19/10/16Planteas bien la regla de Cramer para resolver el sistema de tres ecuaciones con tres incógnitas, pero debes prestar atención a la resolución de los cuatro determinantes, cuya resolución abordas con la regla de Sarrus. Una vez desarrollados, los cálculos quedan (indicamos delta como D):
Ds = (18 + 24 -1) - (4 - 9 + 12) = 41 - 7 = 34, que es distinto de 0, por lo que el sistema es compatible determinado y tiene solución única;
Dx = (24 + 6 - 1) - (4 + 3 - 12) = 29 - (- 5) = 34;
Dy = (- 9 - 8 + 4) - (-2 + 3 - 48) = -13 - (- 47) = 34;
Dz = (6 + 48 + 1) - (8 + 4 + 9) = 55 - 21 = 34.
Luego tenemos:
x = Dx/Ds = 1, y = Dy/D = 1, z = Dz/D = 1, por lo que la solución es la que indica el colega César.
Observando tu fotografía, pareciera ser que has omitido algún signo al plantear los determinantes, y que en algún cálculo siguiendo las diagonales has sumado en lugar de multiplicar, por lo que revisa tus cálculos.
Espero haberte ayudado.
-
Se dispone de una plancha semicircular de 5 cm de radio. De ella se quiere recortar un rectangulo de area maxima, apoyado en el diametro del semicirculo. ¿que superficie tendra el rectangulo quebuscamos? Aqui dejo este problema. Yo he supuesto que el diametro es 10 cm ya que el radio es 5 cm pero no me sale.


Antonio Silvio Palmitano
el 19/10/16Puedes dibujar la semicircunferencia con centro (00) y radio 5, en el semiplano y >= 0, y dibujar en su interior un rectángulo con base en el eje OX, y alturas con puntos terminales en la semicircunferencia, y llamemos (x,y) a uno de dichos puntos. Observa también que la longitud de la base del rectángulo es 2x, su altura es y.
Luego, como las coordenadas del punto cumplen con la ecuación de la semicircunferencia, tenemos:
x^2 + y^2 = 25 (ecuación de la circunferencia), de donde despejamos: y = V(25 - x^2).
Luego, vamos al planteo del área del rectángulo:
A = base*altura
A = 2x*y, sustituimos la expresión para y:
A(x) = 2x*V(25 - x^2) (observa también que el dominio de la función área es el intervalo (0,5)).
Luego, puedes derivar y continuar el trabajo para encontrar extremos para la función.
Espero haberte ayudado.
-
Hola, pueden ayudarme con este ejercicio?
Determinar las constantes a y b de manera que f(x)= { ln(x)-1 si 1≤x≤e ; ax+b si e<x≤e^2 } verifique las condiciones del teorema del valor medio de Langrange en [1,e^2]
Gracias
-
Hola necesito que calculen la inversa de A por el método basado en los determinantes. Por favor respondan hoy ME CORRE MUCHA PRISA MUCHAS GRACIAS y es sencillo. Por favor el examen es mañana



Angie Criollo Zuñiga
el 19/10/16
Cre que te refieres a esto. Pero en sí el ejercicio te pide otra cosa, que es AX+B=C y eso tendrías que ponerlo así: X= A*(C-B)
Con las operaciones que te he hecho yo sería hacer C-B y luego el resultado que me ha dado al final del todo, multiplicarlo por el resultado de C-B.
Espero que lo entiendas... si no, mira este vídeo https://www.youtube.com/watch?v=3BpGef99HEs