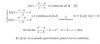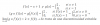-
Fátima
el 15/10/16Me gustaría saber como se hacen las funciones definidas "a trozos"
Miriam
el 15/10/16Aqui tienes uno. Espero que te sirva :)
-
Víctor López
el 15/10/16 -
Juli Ramos Monge
el 15/10/16¿Cómo se haría este límite?
-
Ángela
el 15/10/16 -
Ángela
el 15/10/16Me gustaría saber si el siguiente ejercicio le he realizado bien o si me he equivocado, y en caso de que me haya equivocado, ¿como sería?
Antonio Silvio Palmitano
el 15/10/16Vienes muy bien con mostrar que la función es continua para x = 0, aunque debes precisar cómo resolviste el límite por la derecha.
Con respecto a la derivabilidad, has mostrado bien cuáles son las expresiones para x < 0 y para x > 0, pero para mostrara si existe o no la derivada para x = 0, debes plantear las derivadas laterales aplicando la definición de derivada (límite del cociente incremental).
Haz el intento, y si necesitas vuelves a consultar.
Espero haberte ayudado.
-
Ángela
el 15/10/16 -
Miriam
el 15/10/16Disponemos de una cartulina cuadrada cuyo lado mide 12 cm. Cortamos es las esquinas 4 cuadrados, todos de igual superficie, lo que nos permite, tras doblar, construir una caja abierta. ¿que tamaño deben tener las esquinas para que el volumen de la caja sea máximo? Creo que se trata de optimización, pero no me sale.
Antonio Silvio Palmitano
el 15/10/16Haz un dibujo, y verás que las dimensiones de la caja son:
ancho: 12 - 2x
largo. 12 - 2x
altura: x
Luego, planteamos la expresión de la función volumen:
V(x) = (12-2x)(12-2x)x = x*(12 - 2x)^2
luego planteamos su derivada primera y su derivada segunda:
V ' (x) = (12 - 2x)^2 + x*2*(12 - 2x)*(- 2), que al desarrollar queda:
V ' (x) = 144 - 48x + 4x^2 - 48x + 8x^2, que al reducir términos semejantes queda:
V ' (x) = 12x^2 - 96x + 144 (*)
luego planteamos su derivada segunda:
V ' ' (x) = 24x - 96 (**)
Planteamos luego, a partir de la expresión señalada (*) la condición de punto crítico (singular):
V ' (x) = 0, sustituimos y queda:
12x^2 - 96x + 144 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes las soluciones:
x1 = 6, que no corresponde a este problema, porque conduce a dimensiones (ancho y largo) iguales a cero;
x2 = 2, que al evaluarla en la expresión de la derivada segunda señalada (**) queda:
V ' ' (2) = 24*2 - 96 = -48 < 0, por lo que tenemos concavidad hacia arriba, lo que corresponde a un máximo,
por lo tanto, las dimensiones de la caja con volumen máximo quedan:
ancho: 12 - 2*2 = 8,
largo: 12 - 2*2 = 8,
altura: 2,
y el volumen máximo queda:
V(2) = 8*8*2 = 128.
Espero haberte ayudado.
-
David
el 15/10/16Buenas tardes, ¿me podrían decir si está bien resuelto este ejercicio?
Sean f y g dos funciones reales tales que f(x)=x+1 para todo x real, g(1)=0 y g(x)=2 para todo x real distinto de 1. Estudiar si la función compuesta gºf es continua en x=0.
lim(x→c) f(x) = lim(x→0) x + 1 = 1 ; f(c) es continua
lim[x→f(c)] g(x) = lim(x→1) 0 = 0 ; g[f(c)] es continua
Como se cumplen ambas condiciones, la función gºf es continua en x=0
David
el 15/10/16Muchas gracias Antonio, creo que me ha quedado claro, entonces:
En la función compuesta por partes, lo que primero haces es sustituir cada x por f(x) incluidas las de las condiciones ¿no? y luego, ¿igualas x+1 a 1 para obtener 0?
Y otra duda, al final, en el limite de la función compuesta ¿no sería 0 por la condición de x=0?
Un saludo, gracias.
Antonius Benedictus
el 15/10/16 -
Alex Domínguez
el 15/10/16Pongo una batería de preguntas cortas de matrices , por si podrían ayudarme , Gacias ! ;
En una matriz cuadrada de orden n×n, la tercera columna es 5 veces la primera. En estas condiciones, ¿cuál de las siguientes afirmaciones es correcta?
Seleccione una:a. Su rango es n.b. Su rango es menor que n.c. La matriz se puede invertir.d. Su rango es mayor que n.Sea A una matriz cuadrada de orden n×n y escalonada. Entonces: Seleccione una:
a. Existe la inversa de A.
b. El rango de A coincide con su número de filas no nulas.
c. El rango de A es n.
d. A es regular.
Sea A∈Mm×n(R). Si existe un menor adjunto de A de orden 3×3 no nulo, entonces:
Seleccione una:a. rang(A)≤3b. rang(A)≥3
c. rang(A)=3
d. rang(A)=0En una matriz cuadrada de orden n×n, la tercera columna es 5 veces la primera. En estas condiciones, ¿cuál de las siguientes afirmaciones es correcta?
Seleccione una:a. Su rango es n.b. Su rango es menor que n.c. La matriz se puede invertir.d. Su rango es mayor que n.En una matriz cuadrada de orden n×n, la tercera columna es 5 veces la primera. En estas condiciones, ¿cuál de las siguientes afirmaciones es correcta?
Seleccione una:a. Su rango es n.b. Su rango es menor que n.c. La matriz se puede invertir.d. Su rango es mayor que n.
