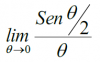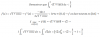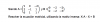-
Hola buenos dias.
Me podrian ayudar con este ejercicio-
En el problema siguiente escriba el numero comlejo, dado en la forma polar usando primero un argumento
teta diferente de Arg(z)y desoues usando
teta=Arg(z)a) 2


Antonio Silvio Palmitano
el 14/10/16Si has escrito bien el apartado a), tenemos al número complejo:
z = 2 + 0i
observa que está representado por el punto de coordenadas (2,0) que se encuentra sobre el semieje OX positivo, luego tenemos:
módulo: |z| = V(2^2 + 0^2) = V(2^2) = 2
tangente del argumento general (indicamos theta como t): tan(t) = 0/2 = 0, luego su argumento general queda:
t = arctan(0) = 360°*k, con k perteneciente a Z (conjunto de los números enteros), por lo tanto su argumento general queda:
arg(z) = 360°*k, que puede tomar los valores: ... - 720°, - 360°, 0°, 360°, 720°, ... (en radianes: ... - 4pi, - 2pi, 0, 2pi, 4pi, ...)
Luego, su argumento principal queda: Arg(z) = 360°*0 = 0° = 0 (en radianes).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 14/10/16Una forma alternativa (observa que el límite es indeterminado, ya que el numerador tiende a 0 al igual que el denominador) es plantear la sustitución (cambio de variable, indicamos theta como t):
w = t/2, de donde tienes: 2w = t, y observa que w tiende a 0 cuando t tiende a 0, luego sustituyes y queda:
Lím(w-->0) senw/(2w) = (1/2)*Lím(w-->0) senw/w = (1/2)*1 = 1/2.
Ya que seguramente has visto en clase que Lím(w-->0) senw/w = 1.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 14/10/16Primero, debes establecer cuál es el mínimo común índice de las raíces, que será el mínimo común múltiplo entre todos los indices de las raíces.
Segundo, llevas tus raíces al mínimo común índice, y elevas sus argumentos (factorizados) con exponente complementario:
(mínimo común índice)/(exponente inicial).
a) Indicamos raíz cuarta con (4V):
Observa que tienes una raíz cuadrada (índice 2) y una raíz cuarta (índice 4), por lo que el mínimo común índice es 4.
Luego tienes:
V(5) = (4V)(5^2)
(4V)(3) ya está expresada con mínimo común índice.
b) Observa que tratas con una raíz cúbica (índice 3), una raíz cuarta (índice 4), y una raíz cuadrada (índice 2), por lo que el mínimo común índice es 12.
Luego tienes:
(3V)(4) = factorizamos el argumento = (3V)(2^2) = reducimos a mínimo común índice = (12V)( (2^2)^4 ) = (12V)(2^8)
(4V)(3) = (12V)(3^3)
V(2) = (12V)(2^6)
Intenta hacer los demás ejercicios, y si te hace falta puedes volver a consultar.
Espero haberte ayudado.
-
Hola a todos tengo que resolver el siguiente ejercicio mi idea para averiguar m y M es hacer la primera derivada e igualar a 0 pero no me estaría saliendo la derivada gracias por su ayuda



Antonio Silvio Palmitano
el 14/10/16Observa que cosx < 1 para todo x real.
Luego, observa que la expresión de la función a integrar toma valores estrictamente positivos en el intervalo [0,1], por lo que podemos plantear:
0 < V(1 + cosx) <= V(1 + 1) = V(2).
Luego integramos miembro a miembro en la doble desigualdad, para el intervalo indicado:
Integral 0*dx < Integral V(1 + cosx)*dx <= Integral V(2)*dx
resolvemos y queda:
0 < Integral V(1 + cosx)*dx <= V(2)*(1 - 0)
resolvemos a la derecha y queda:
0 < Integral V(1 + cosx)*dx <= V(2) < 3/2 (observa que V(2) = 1,4142...< 1,50000... = 3/2).
Por lo tanto concluimos que la integral está acotada entre 0 y 3/2.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 14/10/16Vamos con una orientaciòn. Tienes la ecuaciòn matricial:
X*A - X = B, multiplicamos por derecha al segundo término por la matriz identidad de orden 3:
X*A - X*I = B, extraemos factor común por izquierda en el primer miembro:
X*(A - I) = B
Luego, si la matriz (A - I) es invertible, multiplicamos por derecha por su inversa en ambos miembros:
X*(A - I)*(A - I)^(-1) = B*(A - I)^(-1), resolvemos el producto entre matrices inversas entre si en el primer miembro:
X*I = B*(A - I)^(-1), resolvemos en el primer miembro y llegamos a:
X = B*(A - I)^(-1).
Queda para que hagas todos los càlculos.
Espero haberte ayudado.
-
ayuda compañeros, la integral de e^-x dx