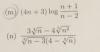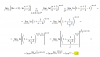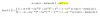-


Antonio Silvio Palmitano
el 15/10/16Observa que tienes tres trozos:
0 para x < 0
x + 0,5 para 0 <= x <= 1
0 para x > 1
luego puedes graficar:
semirrecta: y = 0 a la izquierda del origen (semieje OX negativo), sin incluir el origen
segmento de recta: y = x + 0,5, desde el punto de coordenadas (0 , 0,5) hasta el punto de coordenadas (1 , 1,5) (observa que puedes hacer una tabla de valores)
semirrecta: y = 0, a la derecha del punto de coordenadas (1,0) (porción de semieje OX positivo) sin incluir a dicho punto.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 15/10/16Observa la segunda raíz del denominador en tu planteo, porque luego de sustituir queda igual a z^(1/3).
Observa también que el denominador es una suma de raíz cuadrada con raíz cúbica, y que el mínimo común índice entre ellas es 6, por lo que puedes proponer la sustitución (cambio de variable):
x + 2 = w^6, de donde tienes: dx = 6w^5 * dw, luego sustituyes y la integral queda:
I = Integral ( 6w^5 /(w^3 + w^2) )*dw, que puedes resolver aplicando el método de las fracciones parciales (observa que en este caso debes efectuar la división como primer paso).
Espero haberte ayudado.
-
Me podrian explicar como se hace este ejercicio? Quisiera una pequeña explicacion porque el profesor lo resolvio agarrando 2 vectores li y despues el 3ero uno que sea perpendicular a esos dos.
" Hallar una base de R3 distinta de la estandar"
Muchas gracias!


Antonius Benedictus
el 15/10/16Coges dos vectores no colineales (linealmente independientes) y haces su producto vectorial. El vector resultante, junto a los otros dos, forman una base. Lo justificamos haciendo el determinante formado por los tres vectores, que sería el volumen orientado del paralelepípedo que determinan. Este volumen no es 0, por lo que los tres vectores son linealmente independientes, formando una base de R^3.
-
-
Aqui dejo un problema, si puede alguien que me ayude. Gracias.
Prueba que si w es una raiz compleja n-esima de la unidad, entonces cualquier potencia entera de w es tambien una raiz n-esima de la unidad.