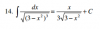-
Alex Domínguez
el 15/10/16Hola, podrían ayudarme con este sistema ? Lo intento pero no me sale
-17x17y0z=a1x1y-1z=32x-3y1z=00x4y1z=2
que valores de a para que sea compatible determinado -
Ismael Garcia
el 15/10/16Muy buenas! Tras varias horas buscando, mirando y tratando de entender esta integral, me ha sido imposible resolverla.
A ver si me la podéis explicar porque aun teniendo la solución no he sido capaz.
Muchas gracias de antemano!
Miriam
el 15/10/16
Antonio Silvio Palmitano
el 15/10/16Va una orientación: puedes plantear la sustitución (cambio de variable):
x = V(3*sent (*), de donde tienes: dx = V(3)*cost*dt, también tienes: 3 - x^2 = 3 - 3*(sent)^2 = 3*( 1 - (sent)^2 ) = 3*(cost)^2 (**).
Luego sustituyes y, luego de operar, la integral queda:
I = (1/3)*Integral (1/(cost)^2)*dt = (1/3)*tant + C.
A partir de las ecuaciones señaladas (*) (**) tenemos que:
(tant)^2 = (sent)^2 / (cost)^2 = (x^2 / 3) / ( (3 - x^2) / 3 ) = x^2 / (3 - x^2), y luego:
tant = V( x^2 / (3 - x^2) ) = x/V(3 - x^2).
Espero haberte ayudado.
-
Alex Domínguez
el 15/10/16Hola, me podrían ayudar con el siguiente problema ?
Sea A una matriz cuadrada de orden n×n y escalonada. Entonces: Seleccione una:
a. Existe la inversa de A.
b. El rango de A coincide con su número de filas no nulas.
c. El rango de A es n.
d. A es regular.
Antonius Benedictus
el 15/10/16Que sea escalonada significa que, reordenando las filas, se puede obtener la forma diagonal o triangular, en la que el determinante es el producto de los elementos de la diagonal principal. Ahora bien, como no se garantiza que éstos sean todos no nulos, rechazamos de plano a), b) y d) que son condiciones equivalentes a que el determinante sea distinto de cero.
El rango de A coincidirá, pues con el número de filas no nulas, que eso, en caso de matriz triangular o diagonal, es siempre correcto.
-
Manuel Mendoza
el 15/10/16Hola chicos, estoi con la hija de una amiga de mi madre que no sabía resolver unas ecuaciones de orden mayor 3, le he explicado Ruffini y bien, pero ha surgido un problema... Tenemos la ecuación: 3x³+3x² -2x+12=0; sé que las raices son: {1.4281, -1.2141 - 1.1520i, -1.2141 + 1.1520i} porque las saque con MatLab... Porque no sé seguir después de aplicar ruffini pq no es exacto nunca... =(
-
diego
el 15/10/16
Hola muy buena unicoos. Me podrian ayudar, Como se haria este limite? El u)
-
Marina Mancera
el 15/10/16 -
Miquel Martos Doroteo
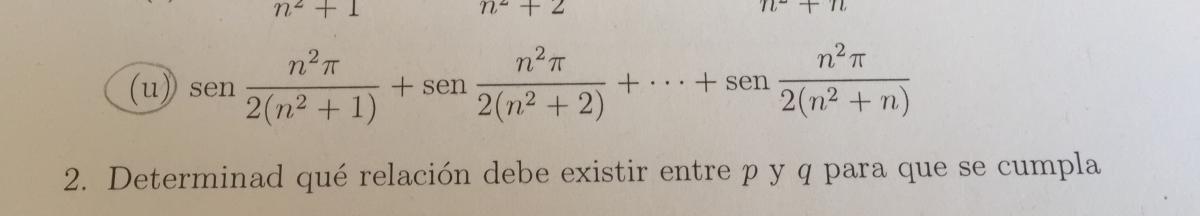
el 15/10/16Buenos días, estoy intentando realizar un ejercicio de vectores en R3, y no se muy bien como terminar el ejercicio, ya que me atasco en un punto. El ejercicio dice así:
Sean u(1, 0, 1) y v(2, 3, -1) dos vectores de R3. Dar dos vectores w1 y w2 ∈ R3 linealmente independientes entre ellos y tales que las familias (u, v, w1) y (u, v, w2) sean linealmente independientes.
He llegado hasta donde les muestro en la fotografía.
Muchas gracias por su tiempo.
Antonio Silvio Palmitano
el 15/10/16Vas muy bien. Observa que has llegado a la condición: x3 - x1 + x2 distinto de 0, que se corresponde con: x3 + x2 distinto de x1. Luego, puedes asignar valores a x3 y a x2, y asignar a x1 un valor distinto de la suma, por ejemplo: x3 = 0, x2 = 0, x1 = 1, y obtienes el vector w1 = <1,0,0>, y si asignas: x3 = 0, x2 = 1, x1 = 2, obtienes el vector w2= < 2,1,0 >.
Espero haberte ayudado.
-
Víctor López
el 15/10/16Buenos días, quería preguntarles sobre este ejercicio de propiedades de determinantes (el 53 de la foto) que no sé muy bien cómo hacer. ¡Gracias!
Miquel Martos Doroteo
el 15/10/16 -
Genesis Guzman
el 15/10/16como puedo calcular los puntos limitantes para graficar el área a calcular si una de las funciones esta elevada al cuadrado?
Antonio Silvio Palmitano
el 15/10/16Puedes pensar en integrar con respecto a y. Para ello, despejas x en ambas ecuaciones, y haces un gráfico "invertido": pones a y como eje horizontal y a x como eje vertical en un sistema cartesiano. Comencemos por despejar x, y las ecuaciones quedan:
y + 1 = x (observa que su gráfica es una recta, que corta en 1 al eje vertical x, y en -1 al eje horizontal y)
(y^2 - 6)/2 = x (observa que su gráfica es una parábola con vértice ubicado en -3 del eje vertical x, que se extiende hacia arriba)
luego observa que la región está limitada "por arriba" por la recta, y "por debajo" por la parábola.
Luego igualamos para determinar los valores de y de los puntos limitantes:
(y^2 - 6)/2 = y +1, hacemos pasaje de divisor como factor y queda:
y^2 - 6 = 2(y+ 1), distribuimos a la derecha y queda:
y^2 - 6 = 2y + 2, hacemos pasajes de términos, reducimos términos semejantes a la izquierda y queda:
y^2 - 2y - 8 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes: y1 = -2, y2 = 4.
Luego, el área limitada por las gráficas de ambas funciones puede calcularse como:
A = Integral ( (y + 1) - ((y^2 - 6)/2 )*dy, en el intervalo [-2,4].
Espero haberte ayudado.
-
Genesis Guzman
el 15/10/16ayuda en este ejercicio pls
Antonio Silvio Palmitano
el 15/10/16Tienes dos modos para resolver este ejercicio:
El primero: resolver la integral (observa que es directa) evaluándola según los límites de integración, y luego derivar
I = Integral ( 1/(1 + t^2)dt = arctant = evaluamos entre x y 1 = arctan1 - arctanx = pi/4 - arctanx;
luego derivamos y queda: I ' = 0 - 1/(1 + x^2) = -1/(1 + x^2).
El segundo consiste en aplicar el Teorema Fundamental del Cálculo Integral (revisa tus apuntes de clase).
Espero haberte ayudado.
