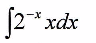-
Hola! Una pregunta que a lo mejor es muy tonta, pero que no veo... ¿cómo despejo λ de z=1+λ/λ? ¡Graciaas!


Antonio Silvio Palmitano
el 12/10/16Si la expresión es (indicamos lambda con L): z = (1+L)/L, observa que L debe ser distinto de cero, luego haces pasaje de divisor como factor y queda:
L*z = 1 + L, luego haces pasaje de término:
L*z - L = 1, luego extraes factor común:
L*(z - 1) = 1, luego haces pasaje de factor como divisor y llegas a:
L = 1/(z - 1), donde z debe ser distinto de 1.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 12/10/16Cuando te presentan a una recta en esta forma, te están mostrando sus ecuaciones cartesianas paramétricas:
x = 2 + L
y = 1 + L
z = 1 + L
tal que L (lambda) es el parámetro, que puede tomar cualquier valor real (para cada valor real corresponde un punto de la recta.
Luego, si el problema consiste en encontrar ecuaciones cartesianas no paramétricas que representen a la recta, debes despejar L a partir de una de las ecuaciones, por ejemplo la tercera: z - 1 = L,
luego sustituyes en las dos primeras ecuaciones y quedan:
x = 2 + z - 1
y = 1 + z - 1
Luego haces pasajes de términos y resuelves, y las ecuaciones quedan:
x - z = 1
y - x = 0
En esta forma, cada ecuación representa un plano, y la intersección entre los planos es la recta.
Espero haberte ayudado
-
Tengo que hacer esta operación:
Pero según un solucionario no esta bien hecha, me la podrían explicar por pasos. Creo que el fallo se encuentra en el 363 pero no se como simplificarlo. GRACIAS


Antonio Silvio Palmitano
el 12/10/16Descomponemos en factores primos, para poder simplificar las raíces donde sea posible, vamos término por término:
V(75) = V(5^2 * 3) = V(5^2)*V(3) = 5*V(3)
2*V(12)= 2*V(2^2 * 3) = 2*V(2^2)*V(3) =2*2*V(3) = 4*V(3)
V(363) = V(11^2* 3) = V(11^2)*V(3) = 11*V(3) (observa que 121 = 11^2)
4*V(3) es mínima expresión.
Luego, tenemos:
V(75) - 2V(12) - V(363) + 4*V(3) =
= 5*V(3) - 4*V(3) - 11*V(3) + 4*V(3) = extraemos factor común:
= (5 - 4 - 11 + 4)*V(3) = resolvemos el agrupamiento:
= - 6*V(3),
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/10/16Observa que puedes escribir: 2^(-x) = ( e^ln2 )^x = e^(ln2*x), para luego plantear la susitución (cambio de variable):
w = ln2*x, de donde tienes: w/ln2 = x, también: dw = ln2*dx, y también tienes: dw/ln2 = dx
Luego sustituyes y la integral queda:
I = Integral ( e^w * w/ln2 ) * dw/ln2 ) = ( 1 / (ln2)^2 ) * Integral (w * e^w * dw) (*)
Seguramente ya has visto en clase que la integral señalada (*) se resuelve por partes, lo haces y llegas a:
I = ( 1 / (ln2)^2 ) * (w*e^w - e^w) + C,
y solo te falta sustituir w por su expresión en función de x.
Espero haberte ayudado.
-
Sea f (x ) = ax3 + bx2 + cx + d , hallar los valores de las constantes a,b,c y d para que la función alcance un máximo de valor 2 en x=-1 y un mínimo de valor -1 en x = 1


Antonio Silvio Palmitano
el 12/10/16Debes tener en cuenta las expresiones:
f ' (x) = 3ax^2 + 2bx + c (para buscar posibles máximos y mínimos), y también f ' ' (x) = 6ax + b (para analizar la concavidad de la gráfica en dichos puntos):
Observa que para el máximo M(x1,y1) tienes:
x1 = 1,
y1 = f(1) = 2, de donde tienes: a + b + c + d = 2 (*)
f ' (1) = 0, de donde tienes: 3a + 2b + c = 0 (**)
f ' ' (1) < 0, de donde tienes 6a + 2b < 0 (***)
y que para el mínimo m((x2,y2) tienes:
x2 = -1
y2 = f(-1) = 1, de donde tienes: - a + b - c + d = 1 (****)
f ' (-1) = 0, de donde tienes: 3a - 2b + c = 0 (****)
f ' ' (-1) < 0, de donde tienes: - 6a + 2b > 0.(******)
Luego, con las ecuaciones señaladas (*) (**) (****) (*****) tienes el sistema de ecuaciones:
a + b + c + d = 2
3a + 2b + c = 0
- a + b - c + d = 1
3a - 2b + c = 0
Queda para que resuelvas el sistema, y para que verifiques que se cumplen las condiciones señaladas (***) (******).
Espero haberte ayudado.
-