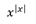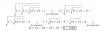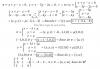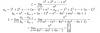-
Alejandro Ballesteros
el 12/10/16 -
Carlos Aray
el 12/10/16Me pueden ayudar con la primera derivada de
Antonio Silvio Palmitano
el 12/10/16Primero reescribamos la expresión de la función (observa que la base debe ser mayor que cero, por lo que el dominio es: D = (0,+inf)):
f(x) = x^|x| = ( e^lnx )^|x| = e^( |x|*lnx ) = e^(x*lnx) (observa que x toma valores estrictamente positivos)
Luego, derivamos con regla de la cadena:
f ' (x) = e^(x*lnx) * ( 1*lnx + x*(1/x) ) = e^(x*lnx) * (lnx + 1) = sustituimos la expresión de la función = x^x * (lnx + 1) = x^|x| * (lnx + 1).
Espero haberte ayudado.
-
Bryan Moreno
el 12/10/16
-
lbp_14
el 12/10/16Hola Unicoos esta operación con fracciones me tiene que dar 3x+2/2x(x+1)
Lo he intentado muchas veces no hay manera de que me de esa solución .
Si me pudieran ayudar se lo agradecería muchísimo .
Antonio Silvio Palmitano
el 12/10/16Vamos con e factor:
A = (x+1)/x - x/(x+2) = extraemos denominador común = ( (x+1)(x+2) - x^2 ) / ( x(x+2) ) = resolvemos = (3x+2)/( x(x+2) )
Vamos con el divisor:
B = 1 + x/(x+2) = extraemos denominador común = (x + 2 + x)/(x+2) = (2x+2)/(x+2) = 2(x+1)/(x+2)
Luego planteamos el cociente:
A/B = A*(1/B) = (3x+2)/( x(x+2) ) * (x+2) / (2(x+1)) = simplificamos = (3x+2) / ( 2x(x+1) ).
Espero haberte ayudado.
-
Andrés Cebrián
el 12/10/16En este video creo que se han calculado determinantes de orden 3 que son redundantes. Solo hay que coger los de orden 3 que incluyan al menor de orden 2 no nulo que hemos conseguido (el método de orlar). Por tanto, solo hay dos de ellos. El que se forma con la tercera fila y la tercera columna prescindiendo de la cuarta columna, y el que se forma con la tercera fila y la cuarta columna prescindiendo de la tercera columna. Como ambos son cero, concluimos más rápidamente que el rango es 2.
Si alguien cree que esté equivocado agradecería un ejemplo donde no ocurra esto. Gracias.
-
Fabrizio
el 12/10/16Hola, no se resolver esto https://gyazo.com/6e93e922034aa1fc56669c03ddaccbdd
Nerea
el 12/10/16Tienes que ir haciendo el cuadrado en ambos lados hasta quitar las raíces:
(√ (1+√ (1+√ (13+√ (x)))))^2 = 2^2
1+√ (1+√ (13+√ (x))) = 4
Y así con todas las veces que haga falta hasta quedarte sin raíces. Una vez tengas eso solo tendrás que resolver la ecuación, es decir, dejar la "x" en un lado y pasar todos los números al otro.
Antonio Silvio Palmitano
el 12/10/16Vamos por pasos, tenemos la expresion:
V ( 1 + V( 1 + V( 13 + V(x) ) ) ) = 2
Primero, haces pasaje de raíz como potencia, resuelves y luego haces pasaje de término, vuelves a resolver y queda:
V( 1 + V( 13 + V(x) ) ) = 4 - 1 = 3
Segundo, haces pasaje de raíz como potencia, resuelves y luego haces pasaje de término, vuelves a resolver y queda:
V( 13 + V(x) ) = 9 - 1 = 8
Tercero, haces pasaje de raíz como potencia, resuelves y luego haces pasaje de término, vuelves a resolver y queda:
V(x) = 64 - 13 = 51
Cuarto, haces pasaje de raíz como potencia y resuelves:
x = 51^2 = 2601.
Espero haberte ayudado.
-
José Rodríguez Lomeña
el 12/10/16Dados en R3 los planos P: x+y-z=0 i Q:x-3y-2z=0, encontrad la base {u,v,w} de R3 tal que {u,v} sea una base de P, {v} sea una base de P∩Q y {v,w} sea una base de Q.
Antonio Silvio Palmitano
el 12/10/16Primero, busquemos la intersección entre los planos P y Q, que es una recta, para ello, elegimos a z = t para parametrizar, y queda el sistema:
x + y = t
x - 3y = 2t
luego resuelves y queda: y = (-1/4)t, x = (5/4)t,
por lo que tenemos que el vector director de la recta intersección es: v = <5/4,-1/4,1>.
Luego, para encontrar un segundo vector del plano P, planteamos dos de sus puntos dándole valores arbitrarios, por ejemplo a x e y:
x=0, y=3, nos conduce a z = 3, y tenemos el punto de coordenadas a(0,3,3);
x=3, y=0, nos conduce a z = 3, y tenemos el punto de coordenadas b(3,0,3),
luego tenemos el vector u = ab = <3,-3,0> (observa que u no es múltiplo escalar de v).
Luego, para encontrar un segundo vector del plano Q, planteamos dos de sus puntos dándole valores arbitrarios, por ejemplo a x e y:
x=0, y=3, nos conduce a z = -9/2, y tenemos el punto de coordenadas c(0,3,-9/2);
x=3, y=0, nos conduce a z = 3/2, y tenemos el punto de coordenadas d(3,0,3/2),
luego tenemos el vector w = cd = <3,-3,6> (observa que w no es múltiplo escalar de v).
Por lo tanto, tenemos una base para R^3:
B ={u,v,w} = { <3,-3,0> , <5/4,-1/4,1> , <3,-3,6> }.
Espero haberte ayudado.
-
salma
el 12/10/16Hola,
Es urgente por favor necesito una ayuda :(
Me podeis ayudar por favor es urgente , se los agradezco. Estoy en primer curso de medecina en Bruselas y necesito resolver este ejercicio por favor .
El período de rotación de la pequeña aguja de un reloj es siempre igual a 12 veces al período de la aguja grande . Un reloj no funciona correctamente. La aguja grande va 1 minuto más por hora para dar una vuelta completa . ¿A qué hora, la primera vez, el ángulo entre las dos agujas es 66◦.
Muchas gracias de antemano
Antonio Silvio Palmitano
el 12/10/16Llamemos w a la velocidad de rotación de la aguja pequeña, y W a la velocidad de rotación de la aguja grande, ambas en condiciones normales:
w = 360°/12h = 30°/h = 30°/60m = (1/2)°/m, en un tiempo t, la aguja pequeña gira un ángulo: a = wt = (1/2)*t
W = 360°/1h = 360°/60m = 6°/m, en un tiempo t, la aguja grande gira un ángulo: A = Wt = 6*t
En condiciones de mal funcionamiento, la velocidad de rotación de la aguja grande es:
W ' = 360°/61m = (360/61)°/m, en un tiempo t, la aguja grande gira un ángulo: A ' = W ' * t = (360/61)*t.
Luego, planteamos
W ´ - w = 66°, reemplazamos y queda:
(360/61)*t - (1/2)*t = 66°, resolvemos a la izquierda:
(659/122)*t = 66°, despejamos:
t = 66° * 122 / 659 = 12,22 minutos, aproximadamente.
Por lo tanto el horario aproximado es: 0h 12m 13s.
Espero haberte ayudado.
-
diego
el 12/10/16Tengo dudas con los ejercicios del Criterio de Stolz, me podria decir alguien donde fallo?. Muchas gracias.
Antonius Benedictus
el 12/10/16 -
Vanesa DeLa Cámara Hernández
el 12/10/16Buenos días, me pueden ayudar a resolver esta ecuación?
x2log2(3+x/2)-x2log1/2(2+3x)=x2-4+2lograizde2((3x2+11x+6)/2)
Soy de 1bachillerato y me han mandado esto para entregar en clase y no entiendo nada...
y también con este otro:
2x*22x+y+3y*8x+y=1
x*22x+y+3y*8x+y=1
En este sistema realizo el cambio de variable de 2x=a y 2y=b y me siguen quedadno un sistema de dos ecuaciones con 4 icognitas, a,b,x,y. me podrian ayudar? muchas gracias!!
