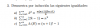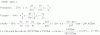-
Barbara Zarate
el 8/10/16Hola!! Necesito ayuda con un ejercicio de la Universidad, es Calculo 1. Limites y derivadas
Dice así: sabiendo que f'(2)=3, comprobar que
Límite cuando x tiende a 2 de (f(x)-f(2))÷(√x-√2) es un numero finito
Antonio Silvio Palmitano
el 9/10/16Observa que tienes como información el valor de la función derivada de la función f para x = 2, que según la definición es:
Lím(x-->2) ( f(x) - f(2) / ( x - 2) = 3 (*).
Luego puedes operar en la expresión que te piden evaluar:
( f(x) - f(2) / ( V(x) - V(2) ) = multiplicamos al numerador y al denominador por el "conjugado" del denominador =
= ( f(x) - f(2) )* ( V(x) + V(2) ) / ( (V(x) - V(2)*(V(x) + V(2) ) = distribuimos y resolvemos el producto en el denominador (observa que nos queda una diferencia de cuadrados) =
= ( f(x) - f(2) )* ( V(x) + V(2) ) / (x - 2) = agrupamos factor y divisor =
= ( f(x) - f(2) )/(x - 2) * ( V(x) + V(2) ).
Luego tomamos el límite para x tendiendo a 2 y queda:
Lím(x-->2) ( f(x) - f(2) )/(x - 2) * ( V(x) + V(2) ) = aplicamos la propiedad del límite de un producto de funciones:
= Lím(x-->2) ( f(x) - f(2) )/(x - 2) * Lím(x-->2) (V(x) + V(2)) = reemplazamos el primer factor según la igualdad señalada (*) y resolvemos el segundo factor:
= 3 * (V(2) + V(2)) = 3*2V(2) = 6V(2) (observa que el resultado es finito).
Espero haberte ayudado.
-
Raisa
el 8/10/16 -
Wayner
el 8/10/16Buenas unicoos, podrian ayudarme en este ejercicio?... la respuesta del ejercicio es: 18 raiz3. Lo hice pero nada que me da la respuesta. Ayudaaa!
Antonio Silvio Palmitano
el 9/10/16Observa que puedes plantear para el ángulo de 60°:
tan60° = h ' / 3 (en el triángulo rectángulo superior más pequeño),
luego, reemplazas el valor de la tangente de 60° y queda:
V(3) = h ' / 3, haces pasaje de divisor como factor y queda:
3V(3) = h '
luego, como sabes que h ' = h/3, reemplazas y queda:
3V(3) = h/3, haces pasaje de divisor como factor, resuelves y queda:
9V(3) = h (*).
Luego, en el triángulo rectángulo inferior puedes plantear:
sen30° = h / |ab|, reemplazas el valor del seno de 30° y queda:
1/2 = h / |ab|, haces pasaje de divisores como factores y queda:
1*|ab| = 2*h, resuelves a la izquierda, reemplazas el valor de h señalado (*) y queda:
|ab| = 2*9V(3), resuelves factores enteros y llegas a:
|ab| = 18V(3).
Espero haberte ayudado.
-
Frank
el 8/10/16ayuda con estas fracciones parciales? 1/{s^2(s^3-9)}
Antonio Silvio Palmitano
el 9/10/16Va la ayuda ( escribimos raíz cúbica como (3V) ): el binomio cúbico s^3 - 9 = ( s - (3V)(9) )*( s^2 + (3V)(9)*s + (3V)(9^2) ).
Recuerda que la diferencia de cubos se factorea: s^3 - a^3 = (s - a)*( s^2 + a*s + a^2 ).
Luego, observa que puedes descomponer en sumas parciales:
1/( s^2 * (s^3 - 9) ) = a / s + b / s^2 + c / ( s - (3V)(9) ) + (d*s + e) / ( s^2 + (3V)(9)*s + (3V)(9^2) ).
Y luego puedes continuar, con un trabajo bastante largo.
Espero haberte ayudado.
-
Carlos Ojeda
el 8/10/16Hoola! Me ayudan con estos ejercicios de demostraciones por inducción
He intentado hacer el primero, pero nada, GRACIAS.
-
Sebastian
el 8/10/16Hola Cesar, el ejercicio es el siguiente. Me piden discutir el sistema, yo a mi manera, saltándome la teoría y todo hice los rangos de D y D* y ambos me han dado como resultado 3, siendo su rango 3, con lo cual es SCD. Pero al ser una matriz de 4X3, intuye que el rango máximo puede ser 3, aunque no se si estoy en lo cierto. Muchas gracias.
-
Usuario eliminado
el 8/10/16Hola alguien podría corregir mi suma superior de rieman
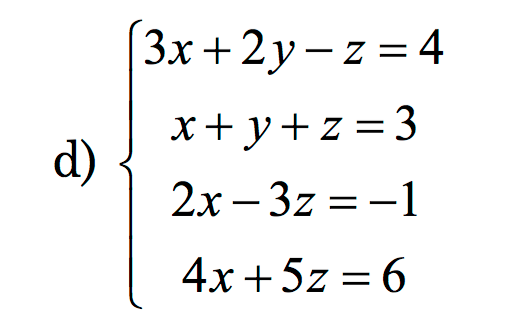
Antonio Silvio Palmitano
el 9/10/16Debes corregir algunas partes de tu planteo. Van algunas orientaciones.
Observa que el área de cada rectángulo de la partición tiene la forma (indicamos delta como D): Ai = Dx*F(xi) = (1/2)*(3*i^2 + 3).
Observa también que para la suma superior, la sumatoria de las áreas de los rectángulos de la partición es entre i=1 e i=6 (si hubiese sido la suma inferior, sería entre i=0 e i=5).
Observa que la longitud de la base en cada intervalo es Dx = 1/2.
Observa que la altura en cada intervalo está determinada por el valor de la función en el extremos derecho del intervalo: hi = F(i), con i entre 1 y 6.
Espero haberte ayudado.
-
Daniela
el 8/10/16 -
Alemberg Bejar Ccama
el 8/10/16 -
peterson
el 8/10/16Buenos dias. Me podriaís ayudar, tengo un problema que no sé como resolver y era por si me podíais ayudar:
Durante el año pasado, un embalse vío como sus reservas variaban de la siguiente forma: .Durante primavera aumentó un 25 %, el verano hizo un 40% y en el otoño aumento un 15 %. Si ahora su volumen es de 150 hm. que volumen tenia el año pasado?¿Cuál ha sido el porcentaje total de variación?
Gracias
