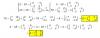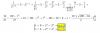thumb_up•0 voto/s

Pon foto original del enunciado, Asd.

Si la ecuación es: arctn(1/x) + arctan(2/x) = pi/2, comencemos por denominar:

a = arctan(1/x) y observa que tana = 1/x (*)

b = arctan(2/x) y observa que tanb = 2/x (**).

Luego, sustituimos y la ecuación queda:

a + b = pi/2, hacemos pasaje de término:

b = pi/2 - a, luego tomamos tangente en ambos miembros:

tanb = tan(pi/2 - a), aplicamos identidad para ángulo complementario:

tanb = cotga, aplicamos identidad para la cotangente:

tanb = 1 / tana, hacemos pasaje de divisor cmo factor:

tana * tanb = 1, sustituimos a partir de las ecuaciones señaladas (*) y (**):

(1/x)*(2/x) = 1, resolvemos en el primer miembro:

2 / x^2 = 1, hacemos pasaje de divisor como factor y queda:

2 = x^2, que nos presenta dos soluciones:

x1 = - V(2), que nos conduce a dos posibles soluciones principales para las incógnitas a y b (expresadas en grados sexagesimales), a partir de las ecuaciones señaladas:

S1: a1 = -35,3°, b1 = 125,3°

S2: a2 = 144,7°, b2 = - 54,7°

x2 = + V(2), que nos conduce a otras dos posibles soluciones principales para las incógnitas a y b (expresadas en grados sexagesimales), a partir de las ecuaciones señaladas:

S3: a3 = 35,3°, b3 = 54,7°

S4: a4 = 215,3°, b4 = -125,3°.

Por lo tanto, las soluciones de la ecuación inicial son: x1 = - V(2) y x2 = V(2),

Espero haberte ayudado.

Disculpe Señor Antonio Silvio pero no entendí por qué tang(pi/2-a) es igual a cotangente de a podría explicarmelo porfavor.

Muchas Gracias y perdón lo otro tengo entendido que la periodicidad de la función tangente es de pi verdad y en pi/2 la función se indetermina ese es uno de mis mayores problemas con el ejercicio.

Perdón y Muchas Gracias :)

Ahí te va

Observa que todas las funciones son continuas en el conjunto de los números reales. Luego, debes buscar valores de x consecutivos para los que cada función tome valores de y con distintos signos:

a) f(0) = -1 < 0 y f(1) = 2 > 0. por lo tanto existe al menos una raíz en el intervalo (0,1).

b) f(-2) = 3 > 0 y f(-1) = -2 < 0, por lo tanto existe al menos una raíz en el intervalo (-2,-1).

c) f(-1) = 2 > 0 y f(0) = - 1 < 0, por lo tanto existe al menos una raíz en el intervalo (-1,0).

En todos los casos hemos aplicado el teorema del valor intermedio.

Espero haberte ayudado.

Sí, Sebastián:

Así es. Cuando desarrollas el determinante te queda un polinomio con variable k, lo igualas a cero para encontrar los valores para los cuales el rango no es 3, y continúas con dichos valores para verificar si el rango es 2 o 1.

Por ejemplo, en el primer ejercicio el determinante queda:

|A| = 0 + k - 2k - (0 + k - 4 + 2k^3) = - 2k^3 - 2k + 4.

Luego, igualamos a 0 y nos queda la ecuación característica:

- 2k^3 - 2k + 4 = 0, observa que una de sus raíces es k1 = 1, luego divides por (k-1) por medio de la regla de Ruffini y queda:

-2k^2 - 2k - 4 = 0, observa que sus raíces no son reales.

Por lo tanto ya sabemos que el rango de la matriz es 3, para k distinto de 1.

Luego, para k igual a 1, la matriz queda:

|  2  1  1  |

|  1  0  1  |

| -2  1 -3 |

cuyo determinante es igual a 0, luego, podemos tomar el subdeterminante formado por los dos primeros elementos de las dos primeras filas y queda:

|  2  1  |

|  1  0  |

lo desarrollas y verás que es igual a -1, distinto de 0.

Por lo tanto, el rango de la matriz es 2 para k = 1.

Espero haberte ayudado.

Es como un sistema normal, Fátima:

Revisa las operaciones, Fabián, que hace mucho que no hago ejercicios de este tipo.

Vamos con una orientación (indicamos diferencia simétrica como ds).

(-->) Sea x perteneciente a A ds B, entonces <por definición de diferencia simétrica>,

(x pertenece a A y x no pertenece a B) o (x no pertenece a A y x pertenece a B) , entonces <por definición de diferencia>

x pertenece a (A-B) o x pertenece a (B-A), entonces <por definición de unión)

x pertenece a (A-B) u (B-A), entonces <por definición de inclusión>

(A ds B) c (A-B)u(B-A) (*)

(<--) Sea x perteneciente a (A-B) u (B-A), entonces <por definición de unión>,

x pertenece a (A-B) o x pertenece a (B-A), entonces <por definición de diferencia>,

(x pertenece a A y x no pertenece a B) o (x pertenece a B y x no pertenece a A), entonces < por definición de diferencia simétrica>,

x pertenece a (A ds B), entonces <por definición de inclusión>

( (A-B)u(B-A) ) c (A ds B) (**)

Finalmente, a partir de las expresiones señaladas (*) y (**) tenemos:

(A ds B) = (A-B)u(B-A).

Espero haberte ayudado.

Comencemos con pasaje de divisor como factor

1 = ( 5 - 2^(x - 1) ) * 2^(x - 3), distribuimos:

1 = 5 * 2^(x - 3) - 2^(x - 1) * 2^(x - 3), aplicamos propiedades de las potencias con bases iguales:

1 = 5 * 2^x * 2^(-3) - 2^(x - 1 + x - 3),

resolvemos factor en el primer término, y reducimos términos semejantes en el exponente del segundo término:

1 = 5 * 1/8 * 2^x - 2^(2x - 4),

resolvemos factores en el primer término y aplicamos propiedad de potencias con bases iguales en el segundo término:

1 = (5/8) * 2^x - 2^(2x) * 2^(-4), resolvemos factor en el segundo término:

1 = (5/8) * 2^x - (1/16)*2^(2x), aplicamos propiedad de la potencia cuya base es otra potencia:

1 = (5/8) * 2^x - (1/16) * ( 2^x )^2, multiplicamos en todos los términos por 16:

16 = 10 * 2^x - (2^x)^2.

Luego hacemos la sustitución (cambio de incógnita): w = 2^x y queda:

16 = 10w - w^2, hacemos pasajes de términos:

w^2 - 10w + 16 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y sus soluciones son:

w1 = 2, de donde tienes: 2^x = 2,^1, y luego: x1 = 1

w2 = 8, de donde tienes: 2^x = 2^3, y luego: x2 = 3

Puedes verificar que las soluciones x1 = 1 y x2 = 3 verifican la ecuación exponencial inicial.

Espero haberte ayudado.

Sin logaritmos, Alofre:

Mírate este vídeo ALOFRE:
http://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/ecuaciones-exponenciales-y-logaritmicas/ecuacion-exponencial 

Veamos las fracciones por separado:

b^2 / (2ab + b^2) = factorizamos en el denominador = b^2/( b(2a + b)) = simplificamos = b/(2a + b)

(ab^2 - 4a^3)/(8a^2 - 2b^2) = factorizamos = a(b^2 - 4a^2)/(2(4a^2 - b^2) = tomamos factor común -1 en el denominador =

= a(b^2 - 4a^2)/(- 2(- 4a^2 + b^2) = simplificamos = a/(-2) = - (1/2)a

1/(4a + 2b) = factorizamos = 1/(2(2a + b)).

Luego planteamos la suma de las dos fracciones del numerador:

b^2 / (2ab + b^2) + (ab^2 - 4a^3)/(8a^2 - 2b^2) = b/(2a + b) - (1/2)a  = tomamos mínimo común denominador =

= (2b - a(2a + b)) / (2(2a + b)) = distribuimos en el numerador = (2b - 2a^2 - ab) / (2(2a + b)).

Luego dividimos por la tercera fracción y queda:

( (2b - 2a^2 - ab) / (2(2a + b)) ) / ( 1/(2(2a + b)) ) = resolvemos =

= (2b - 2a^2 - ab)*2*(2a+b) / ( 2*(2a + b) ) = simplificamos factores =2b - 2a^2 - ab.

Espero haberte ayudado.

Te ayudamos, Diego: