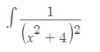→   significa 'Entonces'

↔ Que es equivalente

Para resolver este tipo de ejercicios, hay que demostrar que el primer
conjunto está contenido en el segundo y viceversa. Veamos la solución
del primer ejercicio:

muchísimas gracias aleking 

El rango es 5 , por Gauss Jordan

Muchas gracias, respecto al rango me refería a la otra matriz que he preguntado!

Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?

Para el f) por ejemplo, te sugiero.. 

Vale, muchas gracias.

Te va , es similar en los otros puntos 

prueba a hacer el determinante de la matriz A. Luego igualalo a 0 y obtienes los dos valores de m para los que no existe la inversa de A

Para que el rango de A.B sea 2, debe cumplirse que a.b-c.d≠0. Te vale cualquiera en la que se cumpla eso...
Para que el rango de A.C sea 1 debe cumplirse que a.b-c.d=0.. Te vale cualquiera en la que se cumpla eso siempre y cuando a,b,c,d,e y f no sean iguales a 0... 

Te explicamos, Carmen:

Observa que la expresión de la función puede escribirse:

f(x) = x(x - a) / sen(pix) = ( x/sen(pix)*(x -1) (*) = x * ( (x - 1)/sen(pix) ) (**)

Luego, para estudiar el límite para x tendiendo a 0 por la derecha, empleamos la expresión señalada (*):

f(x) = ( x / sen(pix) ) * (x - 1) = multiplcamos y dividimos por pi = (1/pi) * ( pix / sen(pix) ) * (x - 1)

Y cuando tomas el límite para x tendiendo a 0 por la derecha, aplicamos propiedad del límite de un producto de funciones y queda:

L1 = (1/pi) * Lím(x-->0+)( pix / sen(pix) ) * Lím(x-->0+)(x - 1) = (1/pi)*1*(-1) = -1/pi (***)

Observa que el limite en el segundo factor lo puedes resolver aplicando la sustitución (cambio de variable): w = pix y queda:

Lím(w-->0+)(w/senw) = 1, que es un límite trascendente que has estudiado en clase.

Luego, para estudiar el límite para x tendiendo a 1 por la izquierda, empleamos la expresión señalada (**):

f(x) = x * ( (x - 1)/sen(pix) )

Observa que el denominador del factor fraccionario puede escribirse:

sen(pix) = sen( (pix - pi) + pi ) = identidad trigonométrica = - sen(pix - pi) = - 1* sen( pi(x - 1) ).

Luego, planteamos el límite cuando x tiende a 1 por la izquierda (observa que aplicamos la propiedad del límite de un producto de funciones):

L2 = -1 * Lím(x-->1-)( x ) * Lím(x-->1-)( (x - 1) / sen( pi(x - 1) ) = - 1*1*(1/pi) = -1/pi (****)

Observa que para el límite del tercer factor tenemos:

Lím(x-->1-)( (x - 1) / sen(pi(x - 1)) = multiplicamos y dividimos por pi = (1/pi)*Lím(x-->1-)( pi(x - 1) / sen(pi(x - 1) ) = aplicamos la sustitución: t = pi(x - 1) =

= (1/pi) *  Lím(t-->0-)( t/sent ) = ((1/pi)*1 = 1/pi.

Luego, podemos definir. 

f(0) = -1/pi (a partir del resultado señalado (***))

f(1) = -1/pi (a partir del resultado señalado (****)).

Espero haberte ayudado.

Lo siento pero no entiendo la tabla que aportas... Podría jurarte que los ingresos, siendo X,Y y Z las unidades de cada producto fabricadas, serán 100x+400y+500z
El numero de unidades producidas de x será 90.1+275.4+1700.20... El numero de unidades producidas de Y será 90.2+275.3+40.1700

Por fracciones parciales Jenni :-)

De acuerdo con el colega Peter, y además te sugiero veas los vídeos sobre este método de integración.

Vamos con una orientación para plantear el problema.

Observa que el denominador consiste en un factor doble, que es de grado dos y que no es factorizable en R, por lo que planteamos:

(ax + b) / (x^2 + 4) + (cx + d) / (x^2 + 4)^2 = extraemos denominador común = ( (x^2 + 4)*(ax + b) + cx + d) / (x^2 + 4)^2 = 1 / (x^2 + 4)

Luego, comparando los miembros de la última igualdad de la cadena que hemos planteado, vemos que los denominadores coinciden, por lo que tenemos que los numeradores también deben coincidir, y nos queda la ecuación:

(x^2 + 4)*(ax + b) + cx + d = 1

Y para determinar los valores de los coeficientes a, b, c y d, podemos evaluar para cuatro valores arbitrarios distintos de la incógnita x, lo que nos dejará un sistema de cuatro ecuaciones con cuatro incógnitas para resolver:

4b + d = 1 (hemos evaluado para x = 0)

5a + 5b + c + d = 1 (hemos evaluado para x = 1)

- 5a + 5b - c + d = 1 (hemos evaluado para x = -1)

16a + 8b + 2c + d = 1 (hemos evaluado para x = 2)

Luego, queda para que resuelvas el sistema, y verás que te quedan dos términos para integrar.

Espero haberte ayudado.